Побудувати та знайти площу області. Кратні інтеграли

Наведемо детальний аналіз методики знаходження площі фігури, обмеженої кривими за допомогою кратних інтегралів.
Методика знаходження площі Вам краще запам'ятається в ході розгляду готових прикладів. Площі, що тут будемо обчислювати обмежені прямими, колами, параболами, гіперболами та іншими кривими. З відповідей Ви навчитеся складати системи рівнянь для знаходження точок перетину кривих, правильно розставляти та змінювати порядок інтегрування. Також Ви навчитеся правильно оформляти відповіді до прикладів.

ЗАВДАННЯ 1 Побудувати та знайти площу області D: y=x², x+y=2, x=-1.
Розв'язання: Почнемо з аналізу кривих, що обмежують фігуру:
y=x² - парабола з вершиною у точці O(0;0) і гілками вгору;
x+y=2 - пряма, яка відтинається на осях в точках A(2;0) і B(0;2);
x=-1 - пряма, яка паралельна осі ординат і проходить через точку (-1;0).
Знайдемо точки перетину графіків заданих функцій y=x² і x+y=2:
для цього складаємо систему рівнянь

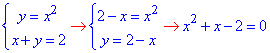
яка після обчислень дає дві точки перетину

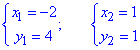
Після цього як знаємо, що за криві задані та їх точки перетину можна приступати до побудови кривих та заштриховування області, площу якої потрібно знайти.

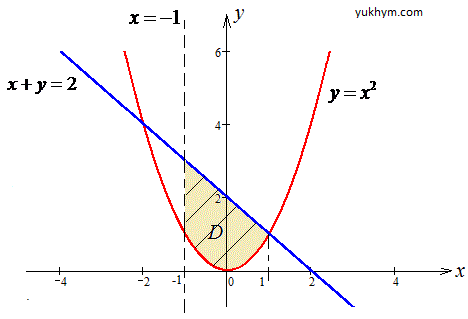
Розставимо межі в заданій області:
D: -1≤x≤1, x²≤y≤2-x .
Обчислимо площу фігури, обмеженої заданими лініями через кратний інтеграл:

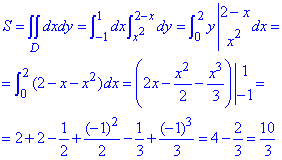
Площа рівна 10/3.

ЗАВДАННЯ 2 Побудувати і знайти площу області D: 4y=x², x+y=3, y=0.
Розв'язання: Проаналізуємо межі фігури:
4y=x², y=x²/4 - парабола з вершиною у точці O(0;0) і гілками вгору;
x+y=3 - пряма, яка відтинається на осях в точках A(3;0) і B(0;3); y=0 - вісь абсцис.
Знайдемо точки перетину графіків заданих функцій 4y=x² і x+y=3:

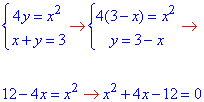
звідси

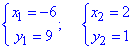
Виконуємо побудову кривих та виділяємо область інтегрування.

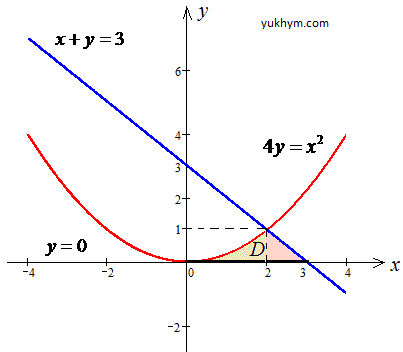
Задану область необхідно розбити на дві області:
D=D₁+D₂.
Розставимо межі в кожній області:
D₁: 0≤x≤2, 0≤y≤x²/4 ;
D₂: 2≤x≤3, 0≤y≤3-x.
Інтегруванням знаходимо площу фігури, обмеженої заданими лініями:

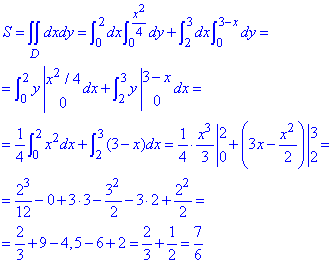
Уважно перегляньте як правильно інтегрувати.
Найменша помилка приводить до неправильного результату, тому уважно інтегруйте та перевіряйте чи знайдена площа відповідає інтегрованій області.

ЗАВДАННЯ 3 Побудувати і знайти площу області D: y=x²+y²-2x, y=x, y=0.
Розв'язання: Зведемо квадратичне рівняння до канонічного вигляду

В результаті зведення під квадрати отримали
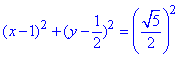- коло з центром у точці O(1;0,5) і радіусом ;
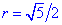y=x- пряма, яка є бісектрисою І і ІІІ координатних чвертей;
y=0 - вісь абсцис.
Знайдемо точки перетину графіків заданих функцій y=x2+y2-2x і y=x:

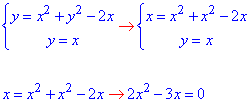
звідси маємо дві точки

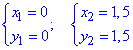
Перетин наступної пари кривих

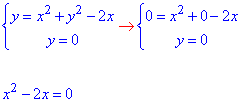
теж дасть дві точки, одна з яких рівна раніше знайденій

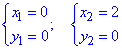
Графік кола та прямих, а також форма області інтегрування мають вигляд:

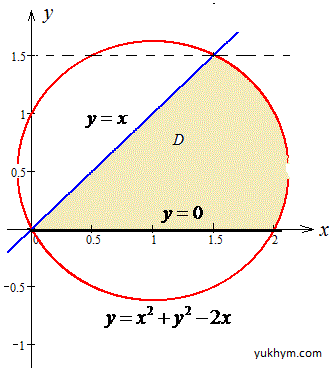
Межі інтегрування, враховуючи розрахунки вище, приймуть значення:
D: 0≤y≤1,5,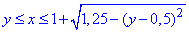
Отож, обчислимо площу фігури, обмеженої заданими лініями:

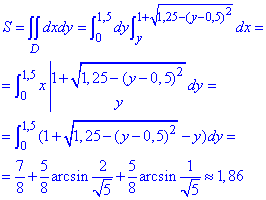
При округленні арксинусів отримаємо, що площа фігури рівна 1,86.

ЗАВДАННЯ 4 Побудувати і знайти площу області D: y³=x, x-y=6, y=0.
Розв'язання: В умові задані:
y³=x - кубічна парабола;
x-y=6- пряма, яка перетинає осі в точках (6;0) і (0;-6);
y=0 - вісь абсцис.
Знайдемо точки перетину графіків перших двох функцій y³=x і x-y=6:

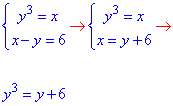
звідси отримаємо точку

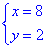
Інші дві точки легко визначити, підставивши рівняння третьої кривої y=0 в рівняння двох перших кривих.
Після цього можемо побудувати фігуру, площу якої шукаємо.

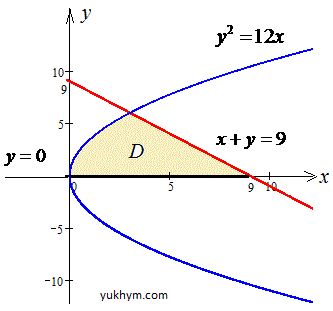
Розставимо межі інтегрування в заданій області:
D: 0≤y≤2, y³≤x≤y+6.
Через кратний інтеграл знаходимо площу фігури, обмеженої заданими лініями:

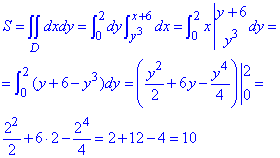
Площа рівна 10.

ЗАВДАННЯ 5 Побудувати і знайти площу області D: y²=4x, x+y=3, y=0.
Розв'язання: Фігура обмежена наступними елементарними кривими:
y²=4x - парабола з вершиною у точці O(0;0) і гілками вправо;
x+y=3 - пряма, яка відтинається на осях в точках A(3;0) і B(0;3);
y=0 - вісь абсцис.
Знайдемо точки перетину графіків першої та другої функцій: y²=4x, x+y=3

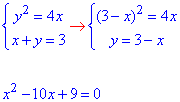
З квадратного рівняння знаходимо дві ординати точок перетину.
Далі, підставленням в друге рівняння системи, знаходимо абсциси "ігрики".

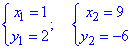
Графік кривих, якими обмежена площа фігури, мають вигляд:

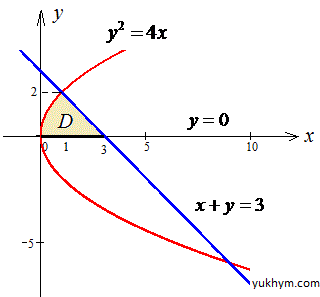
Розставимо межі інтегрування
D: 0≤y≤2, y²/4≤x≤3-y.
Площу фігури знаходимо повторним інтегруванням в області D:

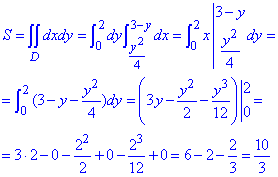
Площа фігури рівна 10/3.

Далі будуть розглянуті більш складні приклади на знаходження площі через кратні інтеграли.