Криволінійний інтеграл I роду. Приклади

Визначені інтеграли у випадках коли інтегрування проводиться не вздовж відрізку, а деякої кривої (на площині чи в просторі) називаються криволінійними. Розрізняють криволінійні інтеграли І та ІІ роду.

Формули криволінійного інтегралу першого роду

Нехай в просторі (чи на площині) задано параметричне рівняння гладкої кривої f(x,y,z)
x=x(t), y=y(t), z=z(t).
tє[a,b].
Кожна з функцій є неперервна на проміжку інтегрування.
Функція f(x,y,z)=0 описує криву в просторі.
Тоді криволінійний інтеграл першого роду рівний інтегралу за параметром від функції помноженої на корінь квадратний з суми квадратів коренів похідних координат за параметром

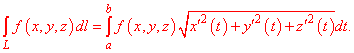
Для випадку кривої на площині формула невизначеного інтегралу І роду спрощується

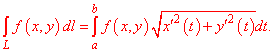
Коли крива інтегрування задана явно y=y(x), формула переходу до визначеного інтегралу має вигляд

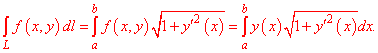
Нехай функція задана полярними координатами rho=rho(phi), phi₁<phi<phi₂. Тоді криволінійний інтеграл першого роду вздовж кривої обчислюється за формулою

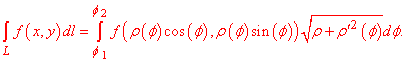
На цьому всі формули, що Вам потрібні для обчислень, однак без готових відповідей важко уявити їх застосування, тому перейдемо до практичної частини.

Обчислення криволінійних інтегралів I роду

Приклади підібрано з навчальної програми для студентів ЛНУ ім. І. Франка. Вони охоплюють широкий клас завдань, які неодмінно зустрінете на контрольній роботі та екзаменах. Тож уважно розберіть відповіді до прикладів та вивчіть наведені вгорі формули знаходження криволінійних інтегралів.

ЗАВДАННЯ 1.7 Обчислити криволінійний інтеграл 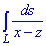вздовж дуги L - відрізок прямої z=x/2-2, що з'єднує точки A(0;-2) та B(4;0) в площині xOz.
Розв'язання: Побудуємо графічно пряму та нанесемо на неї точки, які обмежують дугу

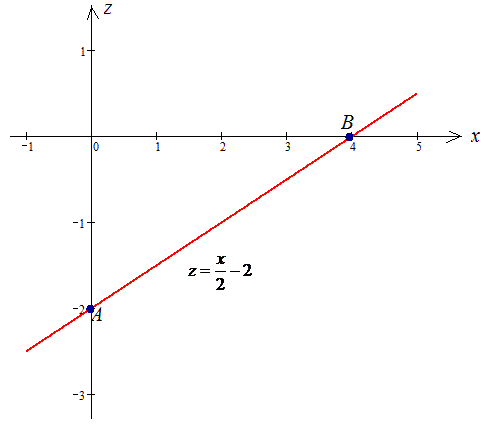
За виглядом бачимо, що необхідно обчислити криволінійний інтеграл І роду.
z=x/2-2, z'=1/2.
Підінтегральна функція прийме значення
1/(x-z)=1/(x-(x/2-2))=1/(0,5x +2).
Знайдемо диференціал дуги заданої кривої за формулою

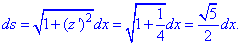
Підставляємо та знаходимо криволінійний інтеграл

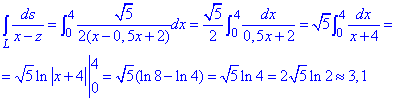
Невизначений інтеграл зводиться до логарифма, який не має особливостей (гладка функція) на проміжку інтегрування.

ЗАВДАННЯ 1.10 Обчислити криволінійний інтеграл вздовж дуги L: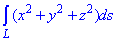
, де L - дуга кривої x=a*cos(t), y=a*sin(t), z=b*t, t[0;2Pi].
Розв'язання: Параметрична крива x=a*cos(t), y=a*sin(t), z=b*t, t[0;2Pi] описує частина гвинтової лінії.
Її графік на циліндричній поверхні має вигляд.

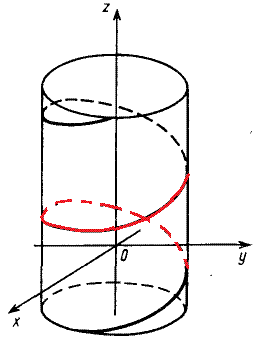
Частина гвинтової лінії, що відповідає проміжку [0;2Pi] зображена червоним кольором.
Підінтегральна функція рівна x²+y²+z².
Потрібно обчислити криволінійний інтеграл І роду. Знаходимо похідні координат за параметром
x'_t=a*sin(t), y'_t=a*sin(t), z'_t=b.
Далі обчислюємо диференціал дуги параметрично заданої кривої згідно формули:

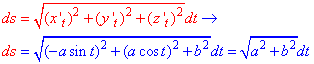
Формула диференціалу дуги в декартовій, полярній та просторовій системах координат приведені в теоретичному матеріалі і тому тут на них затримуватися не будемо.
Інтегруванням обчислюємо криволінійний інтеграл

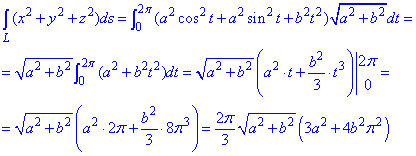
Інтеграл не складний в плані розрахунків.

ЗАВДАННЯ 1.12 Обчислити криволінійний інтеграл 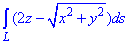вздовж дуги L, де L - дуга кривої x=cos(t), y=sin(t), z=t, [0;2Pi].
Розв'язання: Маємо ідентичне рівняння x=cos(t), y=sin(t), z=t - гвинтової лінії.

Для обчислення криволінійного інтегралу І роду знаходимо похідні координат
x'_t=-sin(t), y'_t=cos(t), z'_t=1.
Підставляємо їх в диференціал дуги гвинтової лінії:

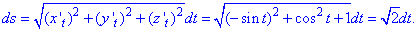
Перетворюємо підінтегральну функцію та знаходимо криволінійний інтеграл

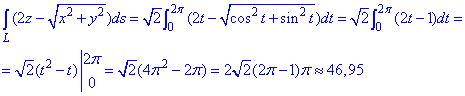
ЗАВДАННЯ 1.14 Обчислити криволінійний інтеграл int(x+y,dS)
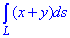вздовж дуги L - дуга кривої x=t, 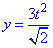, z=t₃, [0;1].
Розв'язання: Перш ніж обчислити криволінійний інтеграл І роду знаходимо похідні за параметром.

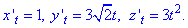
Підставляємо їх в формулу диференціалу дуги:

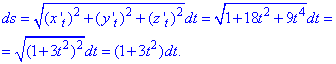
Підставляємо усе у визначений інтеграл та обчислюємо його у вказаних межах

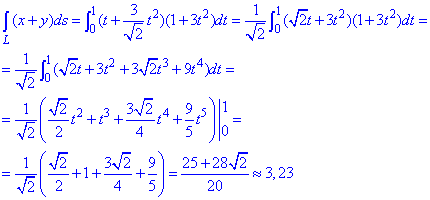
Під інтегралом розкрили дужки і застосували прості формули інтегрування.

ЗАВДАННЯ 1.18 Обчислити криволінійний інтеграл int(1/x²+y²+z²,ds)
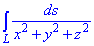вздовж дуги кривої L: x=a*cos(t), y=a*sin(t), z=b*t, t[0;2Pi].
Розв'язання: Інтегрувати знову доведеться вздовж гвинтової лінії.

Похідні за параметром мають вигляд
x'_t=-a*sin(t), y'_t=a*sin(t), z'_t=b.
Обчислюємо диференціал дуги кривої:

Далі перетворюємо криволінійний інтеграл до визначеного та знаходимо його значення

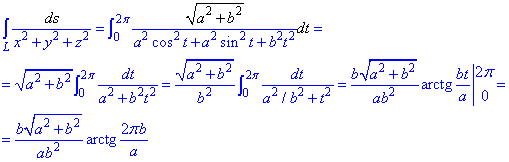
При інтегруванні дістанемо арктангенс. В результаті обчислень отримали компактну формулу через параметри форми циліндра.

ЗАВДАННЯ 1.20 Обчислити криволінійний інтеграл int(x^4/3+y^4/3,ds) вздовж дуги L: дуга астроїди x^2/3+y^2/3=a^2/3.
Розв'язання: Запишемо параметричне рівняння астроїди: x=a*cos³(t), y=a*sin³(t), де t[0;2Pi].
Графік астроїди в декартовій системі координат має вигляд

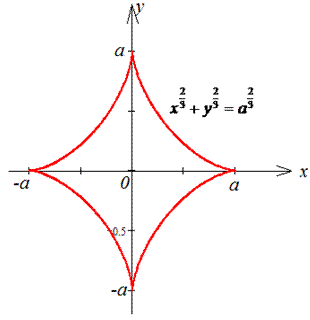
Для обчислення криволінійного інтегралу І роду обчислюємо похідні за параметром
x'_t=-3a*cos²(t)*sin(t), y'_t=3a*cos(t)*sin²(t).
і підставляємо в диференціал дуги астроїди:

Криволінійний інтеграл знаходимо методом заміни змінної

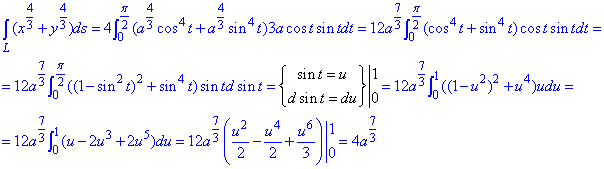
Це дозволяє перейти до простого зрозумілого вигляду підінтегральної функції.

ЗАВДАННЯ 1.21 Обчислити криволінійний інтеграл 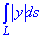вздовж дуги лемніскати (x²+y²)²=a²(x²-y²).
Розв'язання: На лемніскату раніше розглядали інтеграли на знаходження площі.

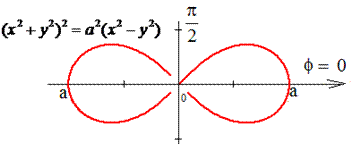
Запишемо рівняння лемніскати в полярній системі координат використовуючи перетворення координат:

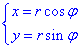
Тоді з рівняння дуги

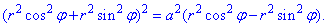
виражаємо радіус вектор та обчислюємо похідну за кутом

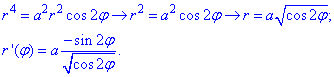
Знайдемо диференціал дуги з формули:

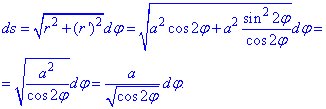
Запишемо підінтегральну функцію: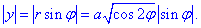
Обчислюємо криволінійний інтеграл І роду як 4 інтеграли по 1 чверті

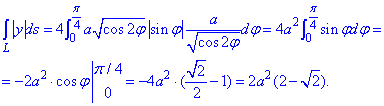
Синус в першій чверті додатний, тому модуль опускаємо.

ЗАВДАННЯ 1.25 Обчислити криволінійний інтеграл вздовж дуги L:
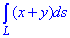, де L - чверть кола x²+y²+z²=R², y=x, що лежить у першому октанті.
Розв'язання: Маємо сферу x²+y²+z²=R² і площину y=x, яка її перетинає.
Графік дуги в просторі має вигляд як на рисунку

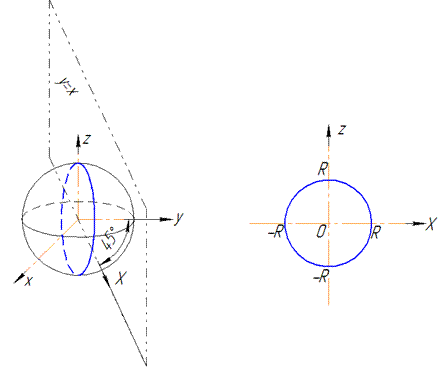
В перерізі отримаємо коло, що проектується на площину y=x рівнянням X²+z²=R², де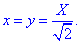
Такі маніпуляції необхідні щоб параметризувати коло
Параметричне рівняння кола: X=R*cos(t), z=R*sin(t) і t[0;Pi/2] (І октант).
Тоді змінні виражаються залежністю

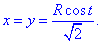
Обчислюємо похідні

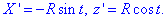
та знаходимо диференціал дуги:

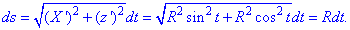
Підставляємо все в інтеграл та виконуємо обчислення

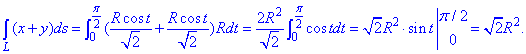
Як Ви могли переконатися нічого складного в знаходженні криволінійних інтегралів 1 роду немає. В теорії відомі формули як переходити від криволінійних до визначених інтегралів, ними і скористалися. Самі ж інтеграли не складні, та й криві на практиці підбираються таким чином, щоб Ви з ними довго не возилися на контрольних чи індивідуальних роботах.
Все зводиться до вміння інтегрувати, що в свою чергу вимагає знання формул інтегрування.