Продовжуємо аналізувати готові приклади на знаходження площі фігур, обмежених прямими, параболами, колами і т.д., через кратні інтеграли.
Складність прикладів полягає в правильному обчисленні точок перетину кривих, вірній розстановці меж інтегрування, розумінні методики обчислення кратних інтегралів. Уважно перегляньте відповіді та саме оформлення пояснень до прикладів, при написанні розрахункових та практичних з інтегрування все має значення: і правильність обчислень, і хід викладу матеріалів.
Уважно перегляньте саме обчислення площ за допомогою інтегрування.
ЗАВДАННЯ 6 Побудувати і знайти площу області D: x2+y2=2y, x=y, x=0.
Розв'язання: Перетворимо рівняння до канонічного вигляду:
x2+y2=2y, x2+(y-1)2=12 - коло з центром у точці (0;1) і радіусом 1;
x=y - пряма,
x=0 - вісь ординат.
Знайдемо точки перетину графіків заданих функцій x2+y2=2y і x=y:
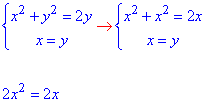
звідси два розв'язки системи рівнянь:

Побудуємо коло та прямі, що обмежують площу фігури.
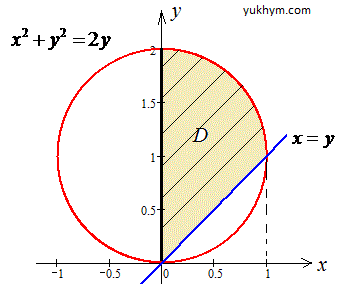
Розставимо межі в заданій області D:
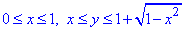
Інтегруванням обчислимо площу фігури, обмеженої заданими лініями:
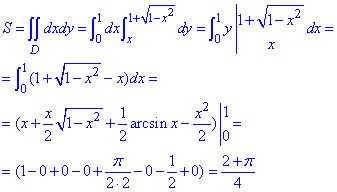
Для того, щоб швидко знаходити площі фігур через кратні фігури варто добре знати таблицю основних інтегралів.
В даному прикладі при інтегруванні отримали арксинус, оскільки інтегрували одну з віток кола.
Також часто Вам доведеться інтегрувати степеневі функції, прямі, що не є складно.
Важче буде з гіперболами та складними показниковими функціями.
ЗАВДАННЯ 7 Побудувати і знайти площу області D: x2+y2=1, x-y=1, y=0.
Розв'язання: Проаналізуємо задані криві:
x2+y2=1 - коло з центром у точці (0;0) і радіусом 1;
x-y=1 - пряма, що відтинається на осях в точках (1;0) і (0;-1).
Складемо систему рівнянь для знаходження точок перетину графіків двох функцій x2+y2=1 і x-y=1:
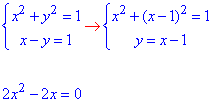
Отримане неповне квадратне рівняння дає два розв'язки:
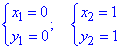
Після того як маємо точки перетину кривих можемо виконувати побудову.
Графік кривих, що задані в умові разом з заштрихованою областю, площу якої потрібно знайти мають вигляд.
Розставимо межі в заштрихованій області D:
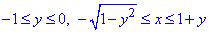
Через кратний інтеграл знаходимо площу фігури:
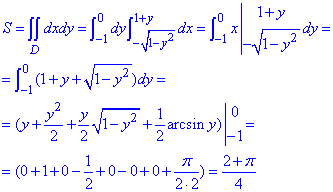
Кінцеве значення площі можна округлити, але це вже виконайте самостійно.
ЗАВДАННЯ 8 Побудувати та знайти площу області D: y=x3+2, y=-x, x=0.
Розв'язання: Знайдемо набір елементарних кривих, що обмежують площу фігури:
y=x3+2 - кубічна парабола;
y=-x - пряма;
x=0 - вісь ординат.
Складемо систему рівнянь та знайдемо точки перетину графіків заданих функцій y=x3+2 і y=-x:
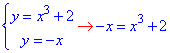
звідси x=-1, y=1.
Виконуємо побудову графіків функцій
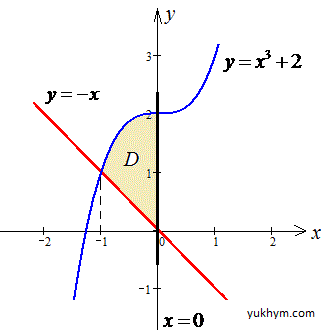
Розставимо межі інтегрування:
D: -1≤x≤0, -x≤y≤x3+2.
Переходимо до знаходження площі фігури інтегруванням:

Інтегрування тут не важка, а площа рівна 10 (одиниць квадратних).
ЗАВДАННЯ 9 Побудувати і знайти площу області D: x•y=1, y=√x, x=2.
Розв'язання:проведемо короткий аналіз заданих кривих.
Маємо x•y=1, y=1/x - гіперболу з гілками у І і ІІІ чвертях;
y=√x - півпараболу з вершиною у точці (0;0) і гілкою вправо;
x=2 - пряму, що паралельна осі ординат.
З перших двох рівнянь кривих складаємо систему рівнянь для знаходження точок перетину графіків функцій xy=1 і y=√x:
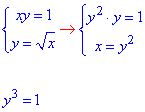
Корінь кубічного рівняння y=1, ордината з другого рівняння x=1 .
Графік гіперболи, параболи та прямої наведені на цьому рисунку:
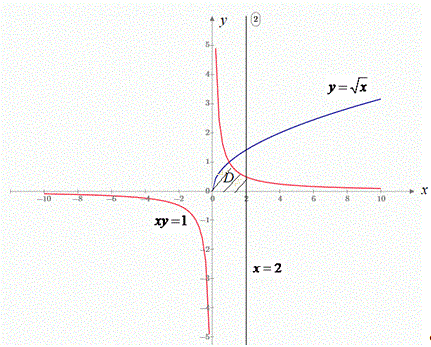
Розставимо межі в області інтегрування D:
1≤x≤2, 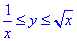
Знайдемо площу фігури, що обмежена заданими лініями:
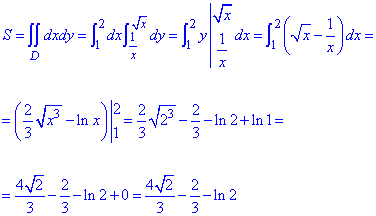
При спрощенні коренів та логарифмів, можна переконатися, що площа додатна.
Ми цього не робили, але повірте, помилки тут немає.
Уважно перегляньте як відбувається інтегрування, від чого залежить по якій з осей краще інтегрувати та як при цьому змінюються межі в кратних інтегралах.


