Сегодня детально проанализируем алгоритм изменения порядка интегрирования в двойном интеграле. Под изменением порядка интегрирования имеем в виду, что задан двойной интеграл в котором интегрирование проводится сначала по "икс", а дальше полученный результат интегрируют по "игрек". Нужно поменять пределы интегрирования, а возможно и разбить на несколько областей интегрирование, для того, чтобы сначала интегрировать по "игрек", а далее по "иксу". В курсе высшей математики подобные примеры учат решать достаточно длительное время, но не во всех это выходит. Схема изменения порядка интегрирования будет расписана на готовых примерах с красиво выполненными рисунками областей интегрирования. Кто-то может подумать, что рисунки здесь ни к чему, но прочитав статью целиком Вы поймете, что без рисунков Вы не сможете понять как изменяются пределы интегрирования, и как их правильно расставлять.
Пример 3.1 Изменить порядок интегрирования в двойном интеграле:

Решение: Построим область интегрирования ограниченую кривыми
0≤x≤4, 3x2≤y≤12x, где
y=3x2 - парабола с вершиной в точке O(0;0) и ветками вверх;
y=12x - прямая, которая проходит через начало координат O(0;0).
График области интегрирования приведен на рисунке.
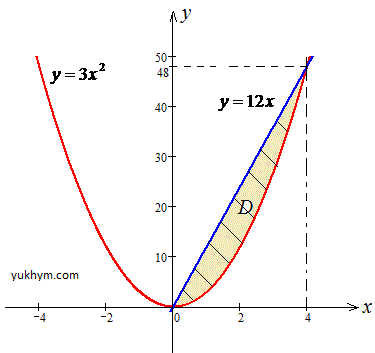
В этом примере "игрек" изменяется от нижней кривой (параболы) к верхней (прямой), в это время "икс" пробегает значение от 0 до 4.
При изменении порядка интегрирования мы будем пробегать значение от первой кривой по "иксу" (прямой) ко второй (параболы), "игрек" в это время будет проходить значение от 0 ко второй точке пересечения заданных кривых.
Отсюда следует, что для изменения порядка интегрирования нужно найти точки пересечения кривых, дальше для изменения пределов нужно перейти от y(x) к x(y) для этих самых пределов.
Выражаем заданные функции y(x) через переменную y:
y=3x2, отсюда 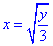 (перед корнем взяли знак "+", поскольку x≥0)
(перед корнем взяли знак "+", поскольку x≥0)
y=12x, отсюда x=y/12.
Найдем точки пересечения:
y=3x2=12x, отсюда
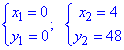
Расставим пределы в заданной области:
D: 0≤y≤48 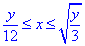
Выполняем изменение порядка интегрирования
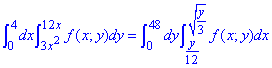
Вот и вся схема перехода от интегрирования по y,x к двойному интегралу по x,y.
Пример 3.2 Изменить порядок интегрирования:
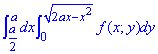
Решение: Запишем область интегрирования для заданного примера
a/2≤x≤a 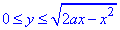 , где y=0 - ось абсцисс.
, где y=0 - ось абсцисс.
Превратим верхнюю кривую по y к каноническому виду
y=√(2ax-x2), y2=2ax-x2, x2-2ax+a2+y2=a2, (x-a)2+y2=a2 - верхний полукруг с центром в начале координат O(a;0) и радиусом a.
На рисунку наведем область интегрирования
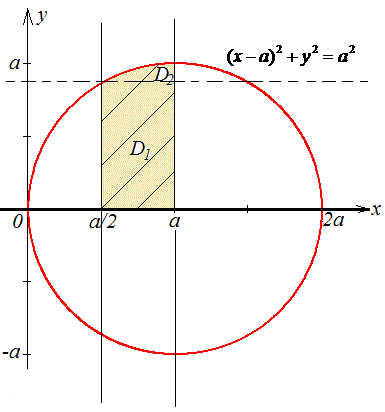
Найдем запись функции через переменную y:
(x-a)^2+y^2=a^2, (x-a)^2 =a^2-y^2,
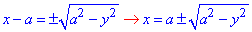
При изменении порядка интегрирования нашу область необходимо разбить на две подобласти:
D=D1+D2.
Расставим пределы в каждой области:
D1: 0≤y≤a√3/2, a/2≤x≤a;
D2: a√3/2≤y≤a, 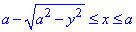
Дальше можем изменить порядок интегрирования
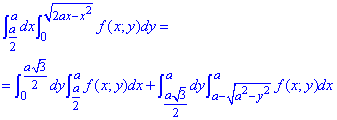
Внимательно пересмотрите фрагмент где область интегрирования разбивается на 2 участка, для чего это делается и от чего зависит.
Многие этого не понимают, поскольку не представляют что делаем, здесь же имеем график из которого видим, что в первой области "икс" изменяется от первой прямой x=a/2 ко второй x=a, во второй области переменная "икс" пробегает значение от полукруга к прямой x=a.
Пример 3.3 Изменить порядок интегрирования:
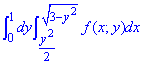
Решение: Область интегрирования ограничена кривыми
0≤y≤1, 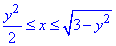 , где x=y2/2 - парабола с вершиной в точке O(0;0) и ветками вправо
, где x=y2/2 - парабола с вершиной в точке O(0;0) и ветками вправо
x=√(3-y2), x2=3-y2, x2+y2=(√3)2 - правый полукруг с центром в точке O(0;0) и радиусом R=√3.
Для изменения порядка интегрирования выражаем функции через переменную x:
x=y2/2, y2=2x, y=√(2x);
x2=3-y2, y2=3-x2, y=√(3-x2).
Найдем точки пересечения графиков функций:
параболы с горизонтальной прямой
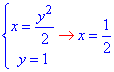
параболы с правой частью полукруга (І четверть)
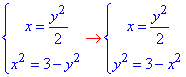
Подставляем y2 из второго уравнения системы уравнений в первое x=1,5-0,5x2;
При решении получим x=1.
Выполняем построение и разбитие на нужные подобласти интегрирования
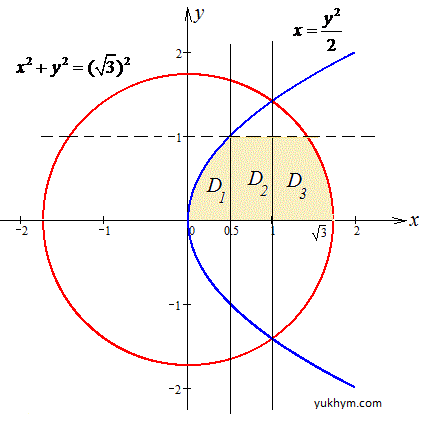
Для изменения порядка интегрирования нашу область разобьем на три подобласти:
D=D1+D2+D3.
Расставим пределы в каждой области:
D1: 0≤x≤0,5, 0≤y≤√(2x);
D2: 0,5≤x≤1, 0≤y≤1;
D3: 1≤x≤√3, 0≤y≤√(3-x2).
Внимательно разберитесь, как это сопоставить с областями на рисунку и почему именно такое разбитие здесь нужно выполнять.
Запишем как изменится интеграл при изменении порядка интегрирования
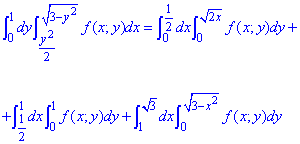
Думаю приведенных объяснений достаточно, чтобы самостоятельно научиться менять порядок интегрирования.
Пример 3.4 Изменить порядок интегрирования:
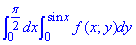
Решение: Построим область интегрирования, которая ограничена кривыми
0≤x≤π/2, 0≤y≤sin(x), где y=0 - ось абсцисс;
y=sin(x) - синусоида.
Выражаемый полученные функции через переменную y:
y=sin(x), отсюда x=arcsin(y);
y=0, отсюда x=0.
Графику кривых наведем на рисунку
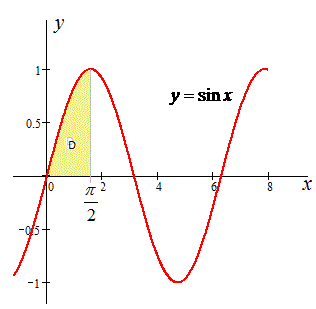
Пределы интегрирования в заданной области поменяются на такие:
D: 0≤y≤1, 0≤x≤arcsin(y).
Записываем двойной интеграл с перечисленными пределами интегрирования
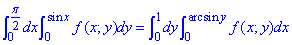
Имеем еще 5 готовых примеров на изменение порядка интегрирования, их Вы можете пересмотреть в следующей статье.


