Площа плоских фігур через криволінійний інтеграл ІІ роду

Криволінійні інтеграли застосовують для обчислення довжини дуг кривих, площі замкнених областей, об'ємів тіл.
Далі проаналізуємо відповіді до прикладів з інтегрування в яких з допомогою криволінійного інтегралу ІІ роду  будемо обчислювати площу еліпса, астроїди, лемніскати.

Завдання 1 За допомогою криволінійного інтегралу обчислити площу, обмежену еліпсом x=a•cos(t), y=b•sin(t) (0≤φ≤2π).
Розв'язання: Перш за все покажемо еліпс, площу якого потрібно знайти

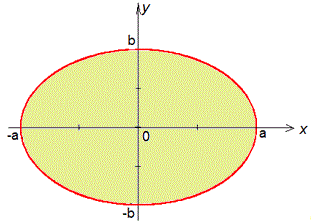
Знайдемо диференціал функції y=b•sin(t) по змінній t:
dy=b•cos(t)dt.
Обчислимо площу еліпса за допомогою криволінійного інтеграла:

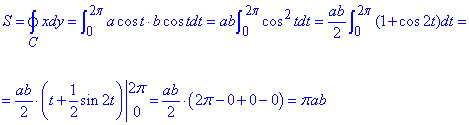
Завдання 2 За допомогою криволінійного інтегралу обчислити площу, обмежену астроїдою x=a•cos³t, y=b•sin³t (0≤φ≤2π).
Розв'язання: В декартовій системі координат астроїда має вигляд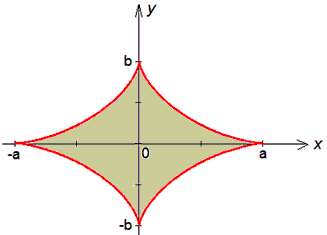

Маємо готове параметризоване рівняння астроїди, тому переходимо до знаходження диференціалу функції y=b•sin³t по змінній t:
dy=3b•sin²(t)•cos(t)dt.
Обчислимо площу еліпса за допомогою криволінійного інтеграла 2 роду:

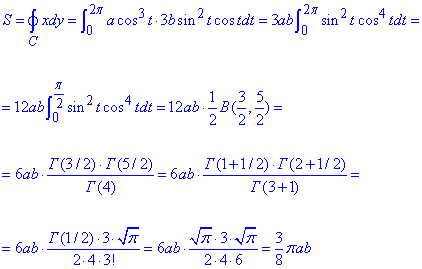
При інтегруванні отримали спеціальні інтеграли Ейлера, які розписані через бета та гамма функції.

Завдання 3 За допомогою криволінійного інтегралу обчислити площу, обмежену лемніскатою (x²+y²)²=a²(x²-y²).
Розв'язання: В прямокутних координатах лемніската має вигляд двох капельок симетрично розміщених відносно осі Oy.

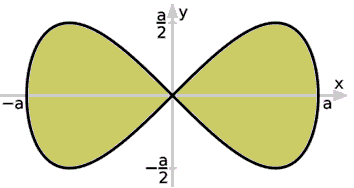
Зведемо задану криву (лемніскату) до параметричного вигляду за допомогою тригонометричної підстановки y=x•tg(φ):

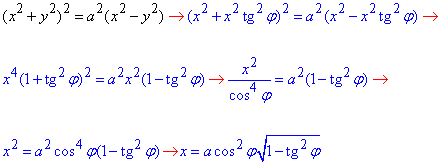
"Ігрик" при цьому прийме значення

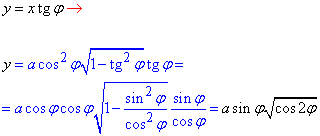
Після усіх перетворень можемо виписати кінцеву параметризацію (це половина лемніскати):

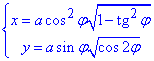
де -π/4≤φ≤π/4.
Знайдемо диференціал від функції 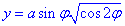по куту φ:

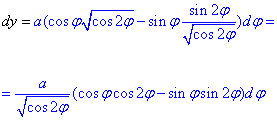
Остаточно диференціал dy рівний

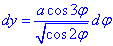
Площу еліпса знайдемо через криволінійний інтеграл другого роду:

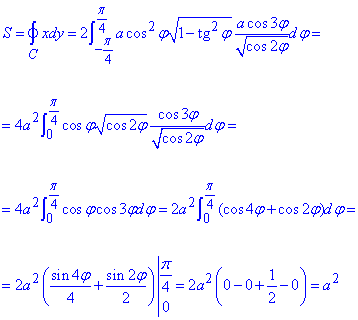
Тут знайшли площу одного пелюстка лемніскати, а результат помножили на 2.
Якщо хочете трохи краще зрозуміти інтегрування то проаналізуйте обчислення інтегралів.
Подібних завдань на знаходження площі плоских фігур через криволінійний інтеграл можна навести безліч. Розглянуті фігури найбільш поширені на практиці.
Крім цього Ви і так бачите, що обчислення в основному полягають:
в параметризації рівнянь, якщо вони складні;
далі визначаємо диференціал та знаходимо криволінійний інтеграл.