Площадь плоскиой фигуры через криволинейный интеграл ІІ рода

Криволинейные интегралы применяют для вычисления длины дуг кривых, площади замкнутых областей, объемов тел.
Дальше проанализируем ответы к примерам на интегрирование в которых с помощью криволинейного интегралу ІІ рода будем вычислять площадь эллипса, астроиды, лемнискаты.

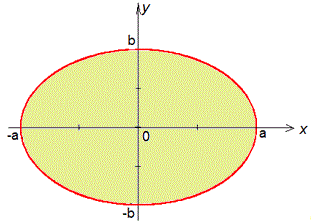
Задание 1 С помощью криволинейного интегралу вычислить площадь, ограниченную эллипсом x=a-cos(t), y=b-sin(t) (0≤φ≤2π).
Решение: Прежде всего нарисуем эллипс, площадь которого нужно найти

Найдем дифференциал координатной функции y=b-sin (t) по переменной t:
dy=b-cos (t) dt.
Вычислим площадь эллипса с помощью криволинейного интеграла:

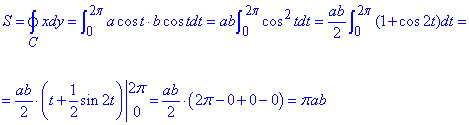
Задание 2 С помощью криволинейного интегралу вычислить площадь астроиды x=a-cos³t, y=b-sin³t (0≤φ≤2π).
Решение: В декартовой системе координат астроида имеет вид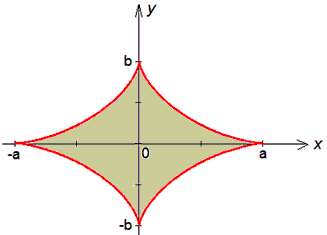

Имеем готовое параметризующее уравнение астроиды, поэтому переходим к нахождению дифференциалу функции y=b-sin³t по переменной t:
dy=3b-sin²(t)-cos(t)dt.
Вычислим площадь эллипса с помощью криволинейного интеграла 2 рода:

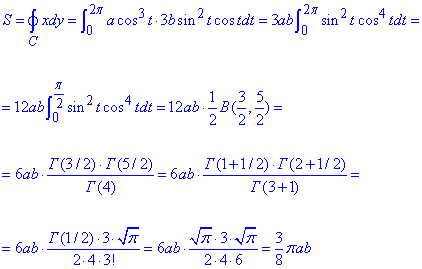
При интегрировании получили специальный интеграл Эйлера, которые расписаны через бета и гамма функции.

Пример 3. С помощью криволинейного интегралу вычислить площадь лемнискаты (x²+y²)²=a²(x²-y²).
Решение: В прямоугольных координатах лемниската имеет вид двух капелек симметрично расположенных относительно оси Oy.

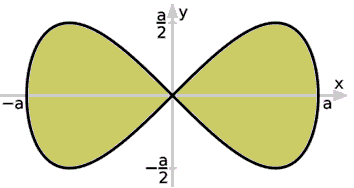
Сведем заданную кривую (лемнискату) к параметрическому виду с помощью тригонометрической подстановки y=x-tg(φ):

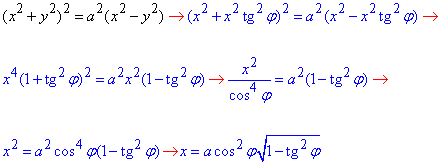
"Игрек" при этом примет значение

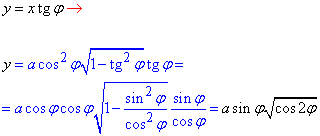
После всех превращений можем выписать конечную параметризацию (это половина лемнискаты) :

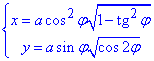
где -π/4≤φ≤π/4.
Найдем дифференциал от функции 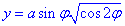по углу φ:

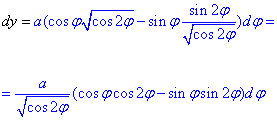
Окончательно дифференциал dy равен

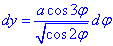
Площадь эллипса найдем через криволинейный интеграл второго рода :

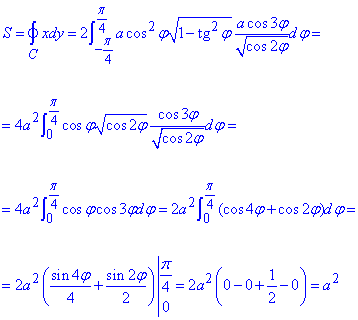
Здесь нашли площадь одного лепесток лемнискаты, а результат умножили на 2.

Если хотите получше понять интегрирование - то проанализируйте вычисление интегралов.
Подобных заданий на нахождение площади плоских фигур через криволинейный интеграл можно навести огромное количество. Рассмотренные фигуры наиболее распространены на практике.
Кроме этого Вы и так видите, что вычисления в основном заключаются:
в параметризации уравнений, если они сложны;
дальше определяем дифференциал и находим криволинейный интеграл.