Формула Гріна. Перехід від криволінійного інтегралу до подвійного

При розв’язанні прикладів з інтегрування є ряд завдань де необхідно перейти від криволінійного інтеграла до подвійного інтеграла й навпаки. Формула Гріна встановлює зв’язок між цими інтегралами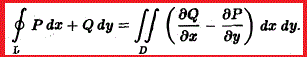

Вона справедлива для будь-якої скінченної замкненої області, яку можна розбити на скінченну кількість правильних для інтегрування областей.
Як це робити на практиці розкриємо в наступних прикладах.

Завдання 1 Використовуючи формулу Гріна, обчислити криволінійний інтеграл:

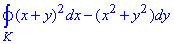
де K - трикутник ABC з вершинами A(1,1), B(3,2), C(2,5).
Розв'язання: Запишемо рівняння сторін трикутника ABC:

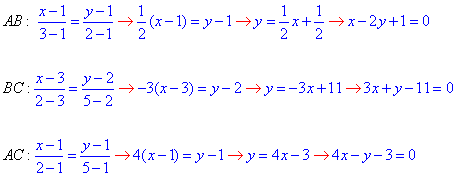
Рівняння потрібні для визначення точок перетину прямих та розділення області інтегрування на підобласті.
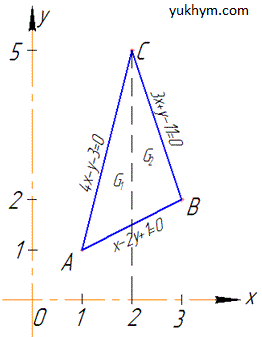
Трикутник в декартовій площині має вигляд

Запишемо підінтегральний вираз:
(x+y)²dx-(x²+y²)dy.
Тут позначимо P=P(x,y)= (x+y)², Q=Q(x,y)=-(x²+y²).
Знайдемо часткові похідні першого порядку функцій P, Q:

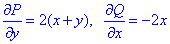
та їх різницю

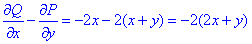
Розставимо межі інтегрування по області G, для цього розділимо її (див. рисунок вище) на дві частини G=G1+G2, тобто
G1: 1≤x≤2, x/2+1/2≤y≤4x-3;
G2: 2≤x≤3, x/2+1/2≤y≤-3x+11.
Уважно погляньте як виконується інтегрування, пам'ятайте - визначення меж в інтегралі відповідальне заняття, адже від них також залежить правильність результату.
Обчислимо криволінійний інтеграл, використовуючи формулу Гріна: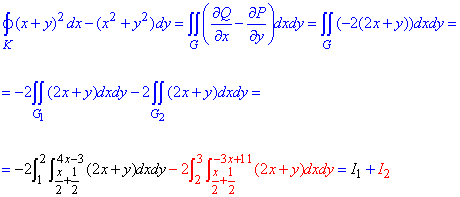

Тут важко вмістити все в одну формулу, та й Вам важко буде її прослідкувати, тому кожен з інтегралів розберемо окремо

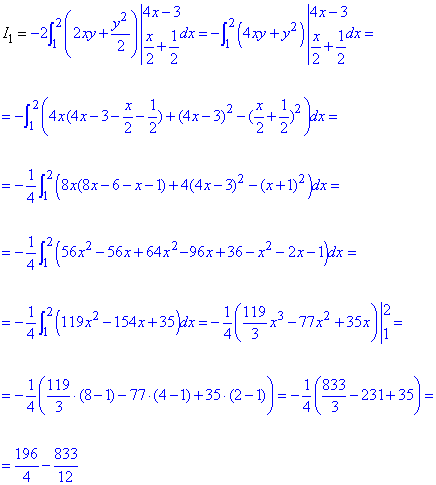
Враховуючи що межі першого інтегралу, що беремо, є функціями дододиться групувати та спрощувати отримані підінтегральні функції.
Подібні маніпуляції виконуємо з другим інтегралом

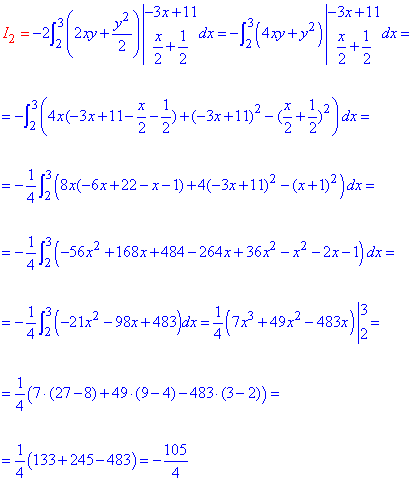
Не забуваємо вкінці обчислити суму інтегралів

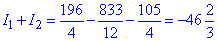
Завдання 2 Використовуючи формулу Гріна, обчислити криволінійний інтеграл:

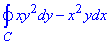
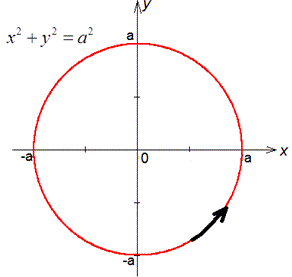
де C - коло x²+y²=a².

Розв'язання: Побудуємо коло вздовж дуги якого шукатимемо інтеграл

Випишемо підінтегральні функції Q=Q(x,y)=xy² та P=P(x,y)=-x²y.
Знайдемо часткові похідні першого порядку функцій Q, P:

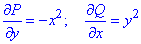
Межі області :
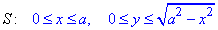і (чверть кола).
Обчислимо заданий криволінійний інтеграл за формулою Гріна:
при інтегруванні виконуємо перехід до полярної системи координат, перераховуємо межі та не забуваємо помножити на якобіан I=r.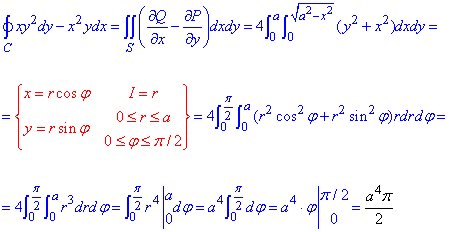
Уважно розберіть як розставляти межі в кратних інтегралах, які методи та коли дозволяють спростити інтегрування.
В майбутньому стаття буде доповнена новими прикладами, але для цього потрібні замовлення від Вас на розрахунок такого сорту інтегралів.