Алгоритм обчислення подвійних інтегралів при переході до полярних координат детально наведений як в цій статті, так і раніше в більш теоретичних публікаціях. Для переходу до полярних координат потрібно знайти якобіан, який кілька раз тут повторимо, далі самі рівняння кривих, що обмежують область інтегрування слід також перевести в полярні координати. В теорії все описано і виглядає зрозумілим, проте на практиці у багатьох виникають труднощі та чимало питань, тому уважно перегляньте наведені далі розв'язки.
ЗАВДАННЯ 2.1 Обчислити подвійний інтеграл, використовуючи полярні координати:
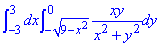
Розв'язання: Побудуємо область інтегрування, яка обмежена кривими
-3≤x≤3,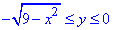 
.
Ці криві записуємо із меж інтегрування, уважно перегляньте в яких межах змінюються "ікс" та "ігрик".
Нижню межу по осі "ігриків" приведемо до канонічного вигляду
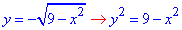
x2+y2=9.
Отримали рівняння кола з центром у точці O(0;0) і радіусом 3 (нижня половина).
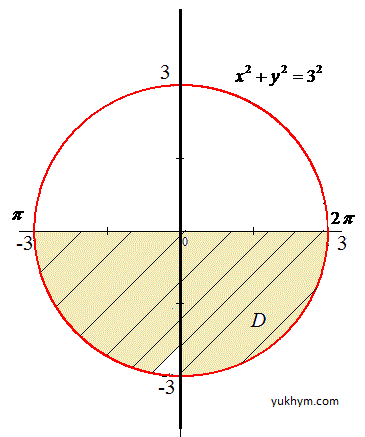
Перейдемо до полярної системи координат за допомогою перетворення координат:
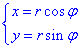
знайдемо якобіан переходу:
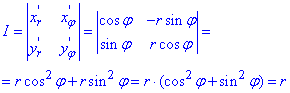
Знайдемо підінтегральну функцію в полярних координатах:
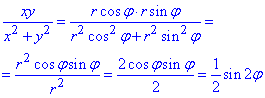
Уважно перегляньте формули подвійного синуса, косинуса і тому подібні. Вони досить часто зустрічаються при спрощенні підінтегральних функцій, все зроблено навмисне для того, щоб Ви без проблем могли інтегрувати.
Запишемо межі інтегрування в полярній системі координат:
0≤r≤3, π≤φ≤2 π.
Обчислимо подвійний інтеграл:
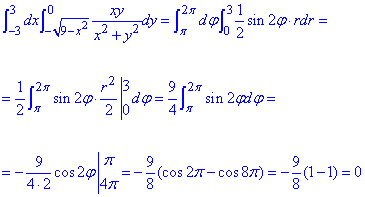
Оскільки змінні розділені то інтегрування не важке, достатньо скористатися табличними інтегралами та підставити межі.
ЗАВДАННЯ 2.2 Знайти подвійний інтеграл, використовуючи полярні координати:
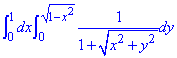
Розв'язання: З інтеграла виписуємо область інтегрування
0≤x≤1,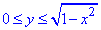 
Вона обмежена прямими, які співпадають з осями координат та
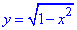, y2=12-x2,x2+y2=12 - дугою кола в І чверті.
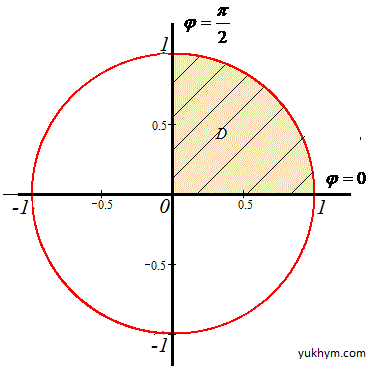
Отримали коло з центром у точці O(0;0) і радіусом r=1 (верхня половина).
Якобіан переходу до ПСК I=r.
Запишемо підінтегральну функцію в полярній системі координат:
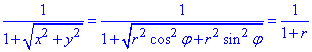
Для кругових областей не важко записати межі інтегрування при переході до полярної системи координат:
0≤r≤1, 0≤φ≤π/2.
Знаходимо подвійний інтеграл:
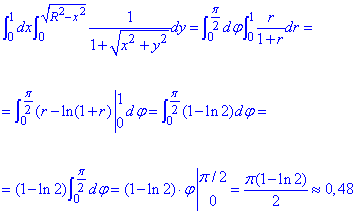
В результаті інтегрування у відповіді отримали логарифм двійки, та число Пі.
ЗАВДАННЯ 2.3 Знайти значення подвійного інтеграла, перейшовши до полярних координат:
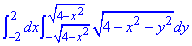
Розв'язання: Випишемо область інтегрування, яка обмежена кривими
-2≤x≤2,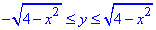 
По "ігрику" маємо обмеження вітками кола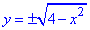 
, y2=4-x2, x2+y2=22 з центром у початку координат O(0;0) і радіусом 2.
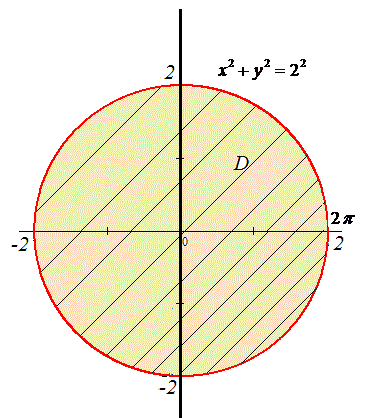
Перейдемо до полярної системи координат:
якобіан переходу: I=r.
При підставленні формул переходу підінтегральна функція в полярній системі координат прийме вигляд кореневої залежності:
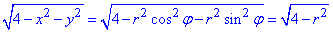
Межі інтегрування в ПСК наступні:
0≤r≤2, 0≤φ≤2π.
Переходимо від подвійного інтеграл в декартових координатах до подвійного в полярних координатах та знаходимо значення:
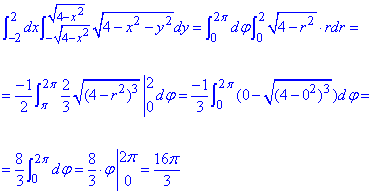
Інтеграл рівний 16π/3.
ЗАВДАННЯ 2.4 Знайти подвійний інтеграл, використовуючи полярні координати:
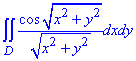
D:{x2+y2=π2/9; x2+y2=π2/4}.
Розв'язання: Випишемо область інтегрування, яка обмежена кривими
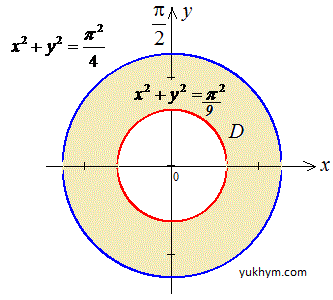
Перша крива x2+y2=π2/9 - коло з центром у точці O(0;0) і радіусом π/3;
друге рівняння описує x2+y2=π2/4 - більше коло з центром у точці O(0;0) і радіусом π/2.
Область між колами утворює кільце, по якому виконуємо інтегрування.
Знайдемо підінтегральну функцію в полярній СК:
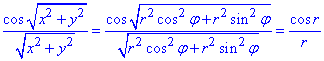
Кола в полярній системі координат можна охарактеризувати радіусами:
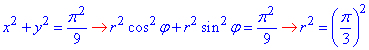, звідси r= π/3;
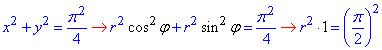, маємо r= π/2.
Межі інтегрування в полярній системі координат наступні:
π/3≤r≤π/2, 0≤φ≤2π.
Виконуємо обчислення подвійного інтеграла:
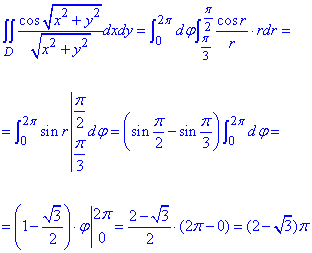
Перехід до полярної СК значно спрощує обчислення інтегралів для кругових та кільцевих областей.
ЗАВДАННЯ 2.5 Знайти подвійний інтеграл, використовуючи полярні координати:
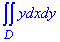
D:{x2+y2-2y=0; x2+y2-4y=0}.
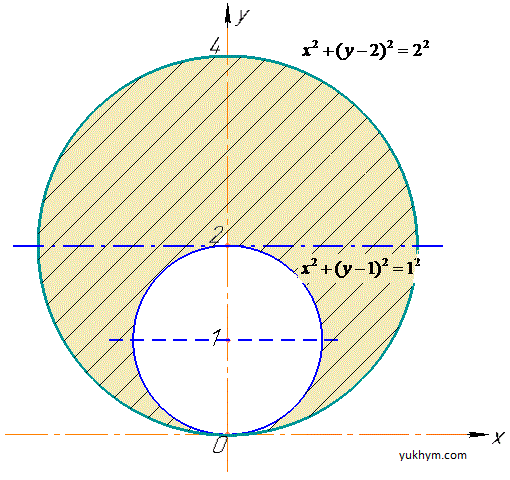
Розв'язання: На основі попередніх прикладів робимо висновок, що область інтегрування, обмежена x2+(y-1)2=1 - колом з центром у точці O(0;1) і радіусом 1;
Друга крива x2+(y-2)2=2- коло з центром у точці O(0;2) і радіусом 2.
Графічно вони формують наступну область інтегрування.
Переходимо до полярної системи координат через якобіан I=r.
Далі записуємо задані криві в полярній системі координат:
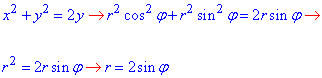
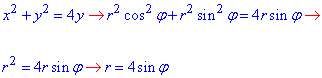
розставляємо коректні межі інтегрування:
2sinφ ≤r≤4sinφ, 0≤φ≤2π.
Обчислюємо подвійний інтеграл в полярній СК:
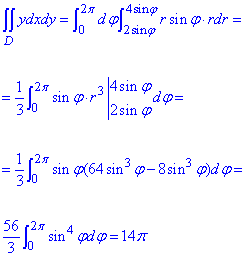
Знаходження подвійних інтегралів не важке, якщо часто цим займатися та мати перед собою таблицю основних інтегралів.
Всі решта маніпуляції не важкі і їх Ви повсюди в математиці виконуєте. Далі розглянемо ще кілька прикладів на обчислення подвійних інтегралів в полярних координатах.
