Обчислення криволінійного інтегралу I роду для плоских кривих

До Вашої уваги добірка готових відповідей на обчислення криволінійних інтегралів вздовж прямолінійних та криволінійних контурів на площині.
Методика розрахунку криволінійних інтегралів наведена раніше і детально розписана.
Тут лише розберемо приклади з практичних для студентів 1,2 курсу та зупинимося на важливих деталях.

Криволінійний інтеграл I роду для кривої заданої в декартових координатах

ЗАВДАННЯ 6.1 Обчислити криволінійний інтеграл:

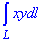
де L - контур |x|+|y|=1.
Розв'язання: Контур |x|+|y|=1 - це квадрат з вершинами в точках A(-1;0), B(0;1), C(1;0), D(0;-1).
Щоб краще уявити вздовж якого контуру інтегруємо, зобразимо лінії, що сполучають задані точки

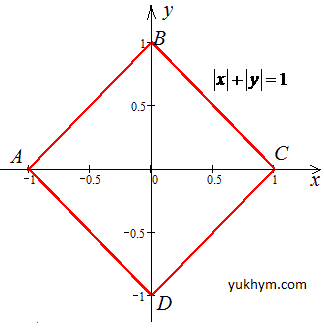
Запишемо рівняння всіх сторін квадрата та їх похідні:
AB: -x+y=1, звідси y=1+x, тоді y'=1;
BC: x+y=1, звідси y=1-x, тоді y'=-1;
CD: x-y=1, звідси y=x-1, тоді y'=1;
AD: -x-y=1, звідси y=-x-1, тоді y'=-1.
Похідні необхідні для обчислення диференціалу дуги кривої:

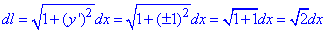
Запишемо межі інтегрування (для кожного відрізка окремо):

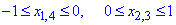
Знаходження криволінійного інтеграла зводимо до сумування 4 визначених інтегралів


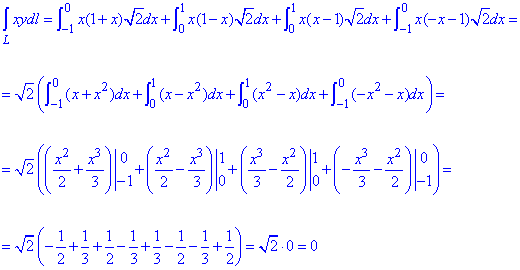
В результаті інтеграл рівний нулю.

ЗАВДАННЯ 6.2 Знайти криволінійний інтеграл:
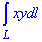, де L - контур прямокутника з вершинами O(0;0), A(4;0), B(4;2), C(0;2).
Розв'язання: Запишемо рівняння сторін прямокутника:
OA: y=0, тоді y'=0;
AB: x=4, тоді x'=0;
BC: y=2, тоді y'=0;
OC: x=0, тоді x'=0.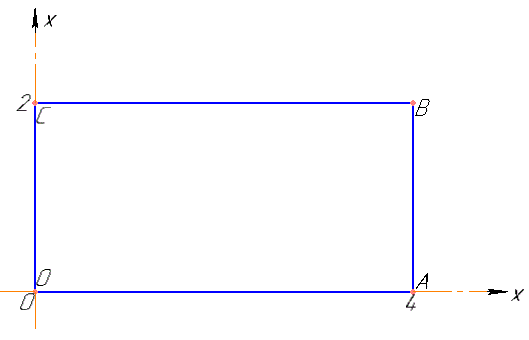
 
Як і в попередніх прикладах, обчислюємо диференціал дуги вздовж сторін прямокутника:
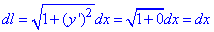і

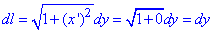
Для цього випадку записуємо межі інтегрування для кожного відрізка окремо:

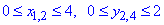
Знаходимо криволінійний інтеграл

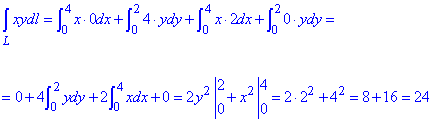
Результат інтегрування рівний I=24.

ЗАВДАННЯ 6.3 Знайти криволінійний інтеграл:
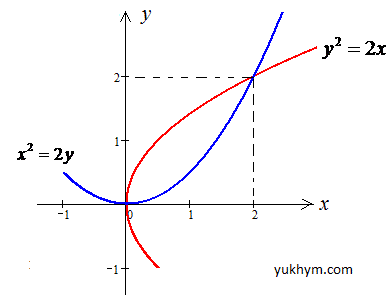
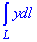, де L - дуга параболи лемніскати y²=2x, яка відтинається параболою x²=2y.
Розв'язання: Знайдемо точки перетину двох парабол y²=2x і x²=2y:
y=x²/2, звідси x⁴/4=2x, x³=8.
Маємо
x₁=0, x₂=2;
y₁=0, y₂=2.
Графік парабол на потрібному нам інтервалі наведено на рисунку

Рівняння параболи, по якій обчислюватимемо криволінійний інтеграл:
,
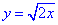звідси похідна

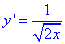
і межі інтегралу 0≤x≤2.
Знайдемо диференціал дуги заданої кривої:

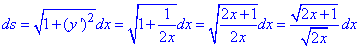
Обчислюємо інтеграл

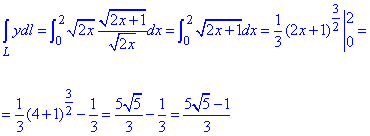
За бажанням можете самостійно округлити отримане значення.

Криволінійний інтеграл для параметрично заданої просторової кривої

ЗАВДАННЯ 6.4 Обчислити криволінійний інтеграл:
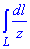, де 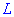- крива пелюсток лемніскати

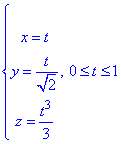
Розв'язання: Маємо просторову криву, що задана параметрично.

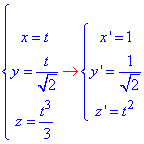
Щоб знайти криволінійний інтеграл обчислимо диференціал дуги за формулою:

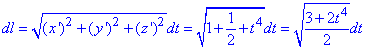
Запишемо підінтегральну функцію:
1/z=3/t³
та межі інтегрування:
0≤t≤1.
Підставляємо в формулу та інтегруємо

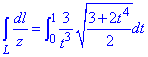
Даний інтеграл не можна подати у вигляді елементарних функцій, тому залишаємо його як є.
В наступній статті розглянемо обчислення криволінійних інтегралів для кривих заданих в полярних координатах, або знаходження таких інтегралів заміною змінних та переходом до полярної СК.