Вычисление криволинейного интеграла I рода для плоских кривых

К Вашему вниманию подборка готовых ответов на вычисление криволинейных интегралов вдоль прямолинейных и криволинейных контуров на плоскости. 

Методика расчета криволинейных интегралов приведена раньше и детально расписана.
Здесь лишь разберем примеры из практических для студентов 1,2 курса и остановимся на важных деталях.

Криволинейный интеграл I рода для кривой заданной в декартовых координатах

Пример 6.1 Вычислить криволинейный интеграл:

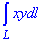
где L - контур |x|+|y|=1.
Решение: Контур |x|+|y|=1 - это квадрат с вершинами в точках A(-1;0), B(0;1), C(1;0), D(0;- 1).
Нарисуєм линии, которые соединяют заданные точки, чтобы лучше представить контур вдоль которого интегрируем

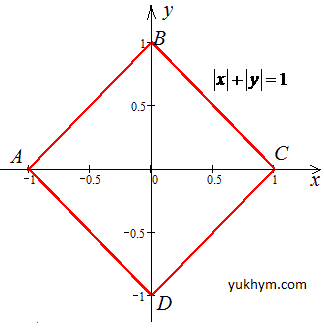
Запишем уравнения всех сторон квадрата и их производные:
AB: -x+y=1, отсюда y=1+x, тогда y'=1;
BC: x+y=1, отсюда y=1-x тогда y'=-1;
CD: x-y=1, отсюда y=x-1, тогда y'=1;
AD: -x-y=1, отсюда y=-x-1, тогда y'=-1.
Производные необходимы для вычисления дифференциала дуги кривой:

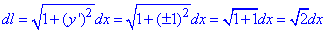
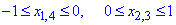
Нахождение криволинейного интеграла сводим к вычислению 4 определенных интегралов


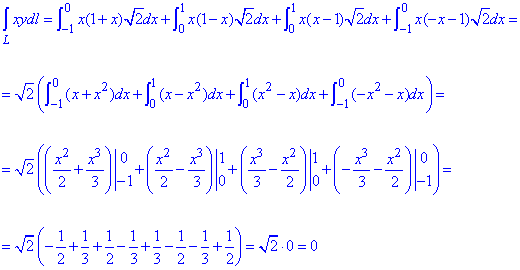
В результате интеграл равен нулю.

Пример 6.2 Найти криволинейный интеграл:
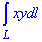, где L - контур прямоугольника с вершинами O(0;0), A(4;0), B(4;2), C(0;2).
Решение: Запишем уравнение сторон прямоугольника:
OA: y=0, тогда y'=0;
AB: x=4, тогда x'=0;
BC: y=2, тогда y'=0;
OC: x=0, тогда x'=0.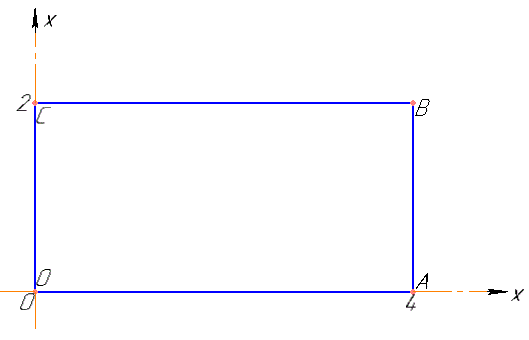

Как и в предыдущих примерах, вычисляем дифференциал дуг вдоль сторон прямоугольника:
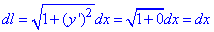и

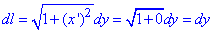
Для этого случая записываем пределы интегрирования для каждой стороны отдельно:

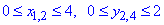
Находим криволинейный интеграл

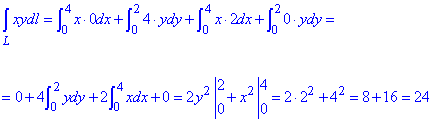
Результат интегрирования равен I=24.

Пример 6.3 Найти криволинейный интеграл:
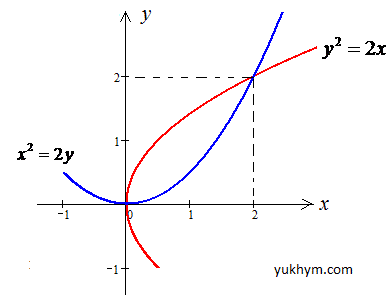
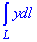, где L - дуга параболы лемнискаты y²=2x, которая отсекается параболой x²=2y.
Решение: Найдем точки пересечения двух парабол y²=2x и x²=2y:
y=x²/2, отсюда x⁴/4=2x, x³=8.
Имеем
x₁=0, x₂=2;
y₁=0, y₂=2.
График парабол на нужном нам интервале приведен на рисунке 

Уравнение параболы по которой будем вычислять криволинейный интеграл:

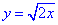
отсюда производная равна

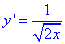
и пределы интеграла 0≤x≤2.
Найдем дифференциал дуги заданной кривой:

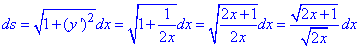
Вычисляем интеграл

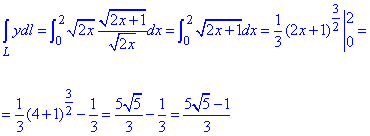
По желанию можете самостоятельно округлить полученное значение.

Криволинейный интеграл для параметрически заданной пространственной кривой

Пример 6.4 Вычислить криволинейный интеграл:
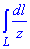, где 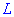- кривая лепестков лемнискаты

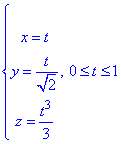
Решение: Имеем пространственную кривую, которая задана параметрически.

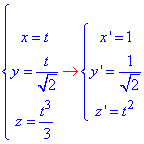
Для интегрирования вычислим дифференциал дуги по формуле:

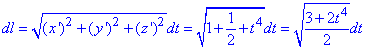
Запишем подынтегральную функцию:
1/z=3/t³
затем пределы интегрирования:
0≤t≤1.
Подставляем в формулу и вычисляем криволинейный интеграл 

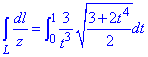
Данный интеграл нельзя подать в виде элементарных функций, поэтому оставляем его как есть.
В следующей статье рассмотрим вычисление криволинейных интегралов для кривых заданных в полярных координатах, или нахождение таких интегралов заменой переменных и переходом к полярной СК.