Обчислення інтегралу ІІ роду між двома точками в просторі

Схема обчислення криволінійного інтегралу другого роду вздовж плоскої кривої раніше добре розписано на основі формули Ньютона-Лейбніца.
Для просторових кривих алгоритм аналогічний, складність полягає в присутності третьої координати.
Таким чином маємо три диференціали, тому щоб два з них зробити рівними нулю контур інтегрування має складатися для двох просторових точок максимум із трьох прямих.
Щоб йти від простого до складнішого розглянемо один приклад криволінійного інтегралу 2 роду вздовж плоскої прямої, а далі 2 від просторової.

Завдання 1 Обчислити криволінійний інтеграл

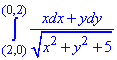
Розв'язання: Маємо двомірний випадок.
Виписуємо підінтегральний вираз:

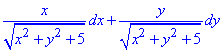
Тут P(x,y) і Q(x,y) рівні

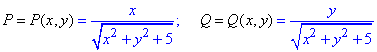
Знайдемо часткові похідні першого порядку функцій P(x,y), Q(x,y):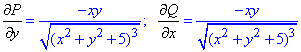

Бачимо, що часткові похідні рівні 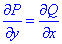, звідси слідує, що підінтегральний вираз є повним диференціалом.
В окремих випадках перевірку на повний диференціал не потрібно виконувати, але це має бути вказано в умові або слідувати з симетричного входження x, y в рівняння P,Q.
Заданий криволінійний інтеграл від точки (2,0) до точки (0,2) будемо обчислювати вздовж прямих x=2 та y=2.
В декартовій площині контур інтегрування має вигляд

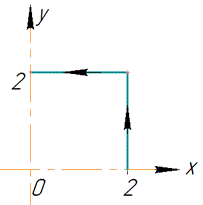
Чому так потрібно вибирати шлях інтегрування описано в статті на яку наведено посилання на початку.
При цьому границі інтегралу та диференціали приймуть значення

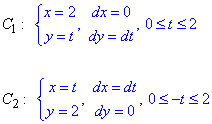
Обчислимо криволінійний інтеграл вздовж плоскої прямої:

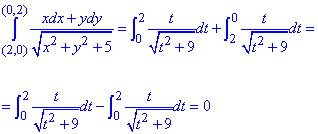
Завдання 2 Знайти криволінійний інтеграл від повного диференціалу просторової кривої:

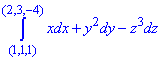
Розв'язання: Для перевірки повного диференціалу функції трьох змінних виписують значення при 3 диференціалах і позначають
P=P(x,y,z)=x, Q=Q(x,y,z)=y², Q=Q(x,y,z)=-z³.
Перегляньте що за що відповідає.
Знайдемо часткові похідні першого порядку функцій P, Q, R за двома іншими змінними ніж присутні в диференціалах при них: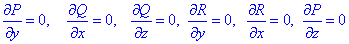

Для того, щоб перевірити, що функція є повним диференціалом слід переконатися, що виконується рівність для 3 пар похідних

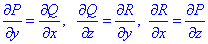
Тут усі часткові похідні рівні нулю, тому підінтегральний вираз є повним диференціалом деякої функції.
Заданий криволінійний інтеграл від точки (1,1,1) до точки (2,3,-4) будемо обчислювати наступним вздовж трьох прямих:

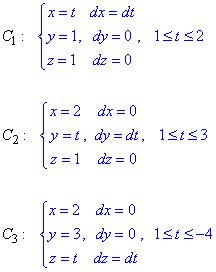
Таким чином ми з першої точки прийдемо в другу рухаючись по прямих, які паралельні осям.
Криволінійний інтеграл 2 порядку вздовж просторової прямої знайдемо з інтегралу:

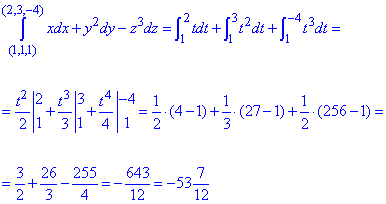
Як бачите, обчислення не важкі.

Завдання 3 Знайти криволінійний інтеграл від повного диференціалу в просторі:

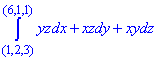
Розв'язання: Випишемо три множники при диференціалах координат
P=P(x,y,z)=yz, Q=Q(x,y,z)=xz, Q=Q(x,y,z)=xy.
Часткові похідні першого порядку функцій P, Q та R рівні:

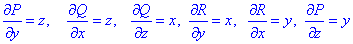
Переконуємось, що виконуються умови рівності часткових похідних

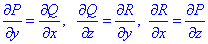
і що дійсно маємо повний диференціал.
Криволінійний інтеграл від точки (1,2,3) до точки (1,1,1) будемо обчислювати вздовж прямих:

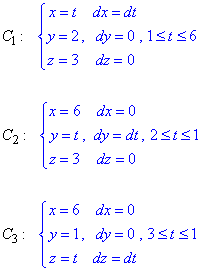
З аналізу можете зауважити, що на кожній прямій два з трьох диференціалів dx, dy, dz рівні нулю. Це можливо завдяки незалежності криволінійних інтегралів від контуру інтегрування.
На площині є два найкоротші шляхи паралельні осям , які дозволяють з однієї точки прийти в іншу. В просторі їх більше на одиницю.
Тому у Вас шлях інтегрування може відрізнятися, проте кінцеве значення інтегралу повинно залишитися рівним.
Обчислимо криволінійний інтеграл ІІ роду вздовж вказаних прямих: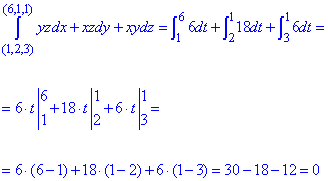

Залишайтеся з нами, попереду ще сотні розв'язаних прикладів з інтегрування.
Думаю, тепер ви зможете повторити наведені розрахунки на аналогічних прикладах!