Обчислення інтегралу першого роду вздовж криволінійних дуг не важко виконати, якщо правильно знайдений диференціал дуги.
Формули для обчислення диференціалу дуги кривої, коли вона задана параметрично, в декартових чи полярних координатах, явно чи неявно розглядалися раніше. Далі розберемо відповіді до прикладів на знаходження криволінійних інтегралів першого роду.
Добре перегляньте інтеграли та розберіть, які методики інтегрування використані в обчисленнях.
Приклад 1 Обчислити криволінійний інтеграл першого роду: int(y-x,s∈C)
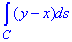, де C - коло x2+y2=4y.
Розв'язання: Запишемо рівняння кола в канонічному вигляді:
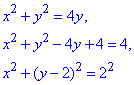
Алгоритм зведення до канонічного вигляду рівнянь 2 порядку Ви повинні знати добре щоб швидко виконувати подібні перетворення, бо такі розрахунки достатньо прості.
З останнього рядка формули бачимо, що маємо коло з центром у точці (0;2) і радіусом R=2.
Для наочності далі маємо рисунок з колом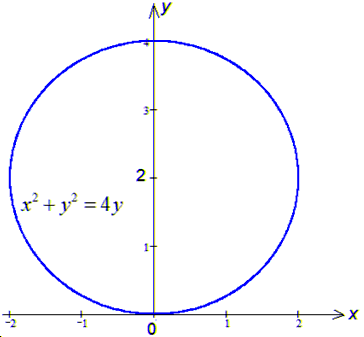
Перейдемо до полярної системи координат за допомогою формул переходу:
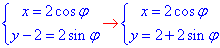(1)
де 0≤φ≤2π.
Заміна змінних тут потрібна для пришвидшення розрахунку диференціалу дуги та інтегралу.
Знайдемо похідні за кутом φ функцій x=x(φ ) і y=y(φ):
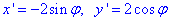
Обчислимо диференціал дуги ds кола за формулою:
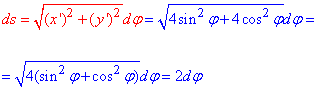
Обчислимо криволінійний інтеграл першого роду вздовж дуги кола:
для цього в підінтегральній функції замінюємо "ігрик" та "ікс" на ті, що в формулах переходу (1), підставляємо знайдений інтеграл дуги та інтегруємо
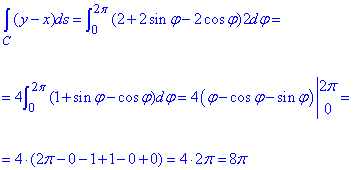
Під інтегралом маємо елементарні функції, які легко інтегрувати.
У випадку обчислень в декартових координатах розрахунки були б складнішими.
Приклад 2 Обчислити криволінійний інтеграл першого роду: int(y2,s∈C)
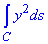, де С - арка циклоїди x=a(t-sin(t)), y=a(1-cos(t)) (0≤t≤2π).
Розв'язання: Циклоїда - це лінія яка описує рух будь-якої точки з кола при його коченні. Оскільки при t=0 значення x,y рівні нулю, то в початковий момент часу маємо нижню точку кола. Графік заданої астроїди має вигляд
Обчислимо похідні по змінній t від заданих функцій x=x(t) та y=y(t):
Знайдемо диференціал дуги ds циклоїди за формулою:
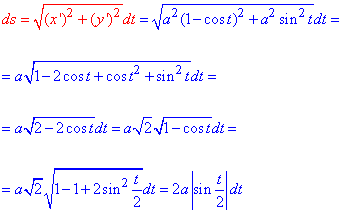
Обчислимо криволінійний інтеграл першого роду по дузі циклоїди:
потрібні переходи виділені в формулі кольорами
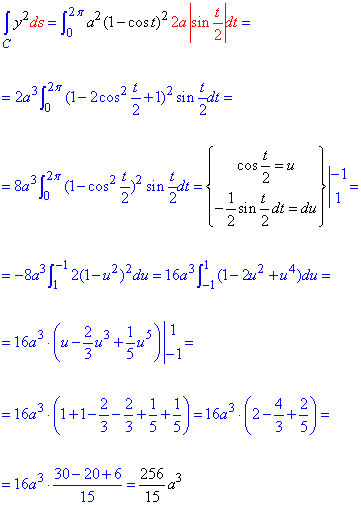
Під інтегралом виконали заміну змінних та перейшли до інтегрування частинами. При заміні змінних не забувайте перераховувати межі інтегрування, доволі часто така помилка зустрічається у студентів.
Приклад 3 Обчислити криволінійний інтеграл першого роду: int(xy,s∈C)
, де С - дуга гіперболи x=a•ch(t), y=a•sh(t) (0≤t≤0).
Розв'язання: Наведемо графік гіперболи в декартових координатах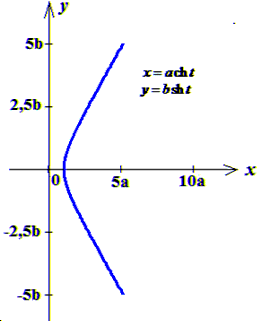
Знайдемо похідні по змінній t від заданих функцій x=x(t) і y=y(t):
x'=a•sh(t), y'=a•ch(t)
Плюсом гіперболічних функцій при диференціюванні є те, що похідна від гіперболічного косинуса рівна гіперболічному синусу і навпаки.
Диференціал дуги ds гіперболи обчислимо за формулою:
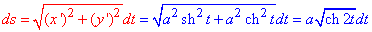
Обчислимо криволінійний інтеграл першого роду по дузі гіперболи:
"ікс, ігрик" під інтегралом міняємо на ті, що є в рівнянні гіперболи, далі підставляємо диференціал по дузі та інтегруємо
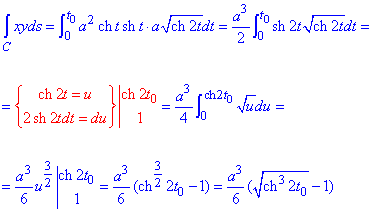
Тут, як і в попередньому прикладі, заміна змінних та інтегрування частинами допомагають знайти криволінійний інтеграл.
Приклад 4 Знайти криволінійний інтеграл першого роду: int(1/y2,s∈C)
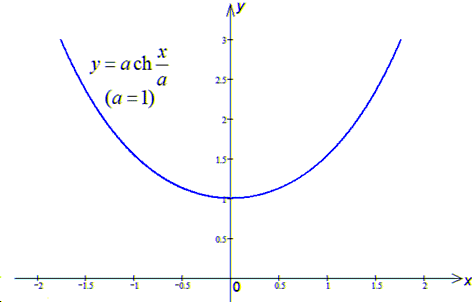
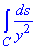, де C - ланцюгова лінія y=a•ch(x/a).
Розв'язання: Наведемо графік кривої вздовж якої будемо інтегрувати
Знайдемо похідну по змінній x від заданої функції y=y(x):
y'=sh(x/a)
Оскільки в умові завдання обмежень по x немає, то приймаємо що змінна пробігає значення від мінус безмежності до плюс безмежності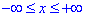 
.
Диференціал дуги ds ланцюгової лінії знайдемо з формули:
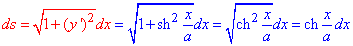
Обчислимо криволінійний інтеграл першого роду вздовж ланцюгової лінії:
замінюємо "ігрик" в інтегралі на рівняння ланцюгової лінії, підставляємо диференціал дуги та інтегруємо
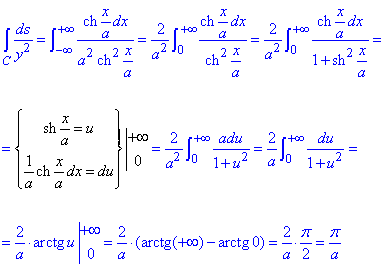
І знову прийшлось інтегрувати частинами.
Якщо у прикладах, що Вам задали, функції під інтегралом відрізняються від тих що тут розглянуті, то просто їх перераховуєте підстановкою відповідних дуг, а все решта (диференціали дуг, алгоритми обчислення інтегралів) виконуєте у відповідності з наведеними поясненнями.
Детально перегляньте наведені відповіді та розберіть методи, які застосовували при інтегруванні.
Попереду Вас чекають ще сотні готових прикладів з інтегрування.
