За формулами інтегрування інтеграл від синуса sin(x) рівний косинусу, причому зі знаком мінус. Багато хто часто допускає помилки бо не може запам'ятати, що похідна від синуса рівна косинусу, а від косинуса – синусу зі знаком мінус.
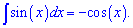Хто вивчає первісну, то до правої сторони слід додати сталу
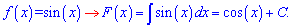Сталу визначають з додаткової умови.
Графік синуса має вигляд
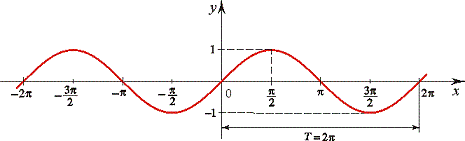
Синус непарний, а косинус – парна функція, тому при інтегруванні з'являється знак мінус. На початку всім здається все простим і зрозумілим. Та настає час ускладнювати інтеграл, тобто інтегрувати синус подвійного кута, потрійного аргументу і т.д. І в багатьох виникають труднощі з інтегруванням. Для виведення формули для sin(k*x) проведемо всі викладки спочатку. Для того, щоб звести інтеграл до табличної формули треба внести коефіцієнт під диференціал, але це змінить сам інтеграл. Тому одночасно ділимо на коефіцієнт
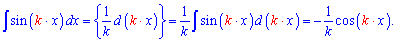
Знаючи цю формулу, інтеграл від синуса подвійного кута записуємо одним рядком
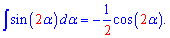Далі можемо проінтегрувати синус потрійного кута
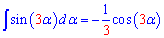і так далі
int(sin(k*x)=-1/k*cos(k*x).
За такою ж формулою виводять інтеграл від синуса половини кута, який рівний мінус 2 косинус половини кута.
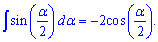Інтеграл від синуса однієї третьої х рівний
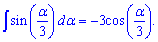
Поширені приклади інтегрування синуса
Приклад 1. Знайти інтеграл від sin(4*x).
Обчислення: За формулою інтегрування знаходимо
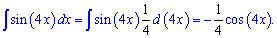
Приклад 2. Обчислити інтеграл від sin(5*x).
Обчислення: Виконуємо інтегрування
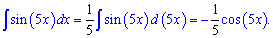
Приклад 3. Проінтегрувати вираз sin(7*x).
Обчислення: Знаходимо неозначений інтеграл
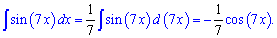
Приклад 4. Знайти інтеграл від функції y=sin(x/5).
Обчислення: Знаходимо неозначений інтеграл
Як тільки Ви навчитеся обчислювати прості інтеграли від синуса можете переходити до визначений інтегралів
Приклад 5. Знайти первісну від sin(x), яка в нулі рівна 2.
Обчислення: Обчислюємо первісну
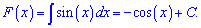
З умови на первісну знаходимо сталу
-cos(0)+C=2;
C=2+cos(0)=3.
Повертаємося до первісної та підставляємо знайдену сталу
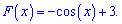
це і відповідь до завдання. Як тільки Ви навчитеся обчислювати прості інтеграли від синуса можете переходити до визначений інтегралів
Приклад 6. Проінтегрувати синус подвійного кута y=sin(2*x) від 0 до 45 градусів.
Обчислення: Записуємо інтеграл від синуса та підставляємо межі інтегрування
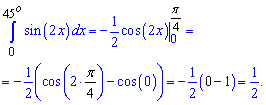
За фізичним змістом визначений інтеграл рівний площі фігури обмеженої функцією sin(x) та віссю абсцис.
Але визначений інтеграл і площа, це не одне і те саме Інтеграл може бути від'ємним, а площа ні. Якщо функція більшу площу має під віссю абсцис, то її означений інтеграл від'ємний.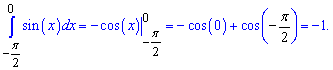 
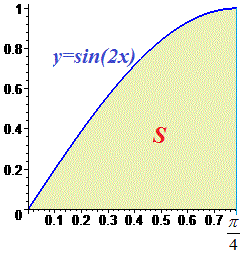
Площа криволінійної трапеції рівна інтегралу від різниці верхньої кривої і нижньої.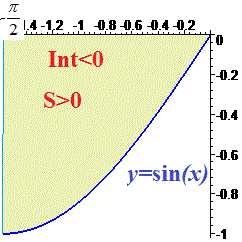 
В даному випадку верхня крива це вісь абсцис або y=0. Нижня – це графік синуса. Тому формула площі синус функції рівна 1, або визначеному інтегралу за модулем.
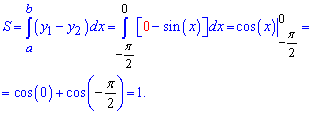
Якщо функція антисиметрична відносно осі абсцис, то її інтеграл рівний нулю, а площа рівна подвійному інтегралу графіка над віссю абсцис. На прикладі синуса подвійного кута інтеграл від -45 до 45 градусів рівний нулю
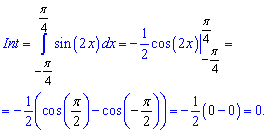
В той же час площа заштрихованої фігури рівна одиниці.
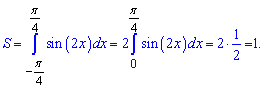
На графіку це матиме вигляд.
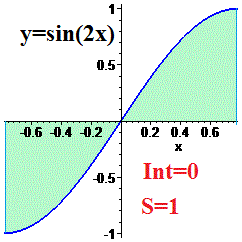З наступних матеріалів Ви дізнаєтесь, як знайти інтеграл від функцій виду
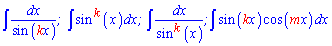які формули згортки та заміни змінних при цьому слід використовувати. Також Ви оволодієте методикою обчислення інтегралів виду
де Pm(x) - поліном від змінної. В таких випадках застосовують інтегрування частинами, але про це піде мова пізніше.
А на цьому ознайомлення з інтегруванням синуса завершується. Інтеграли від інших тригонометричних та обернених до них функцій Ви знайдете на сторінках категорії "Інтегрування функції".
