Робота сили через криволінійний інтеграл ІІ роду

Продовжуємо попередній урок на тему "Застосування криволінійних інтегралів 2 роду".
Готові відповіді задач на роботу силового поля допоможуть студентам вивчити тему, та навчать швидко знаходити потрібні інтеграл.

ЗАВДАННЯ 4.2 Знайти роботу сили F (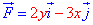) при переміщенні вздовж кривої C: x²/4+y²/9=1 від точки A(-2;0) до точки B(0;3).
Розв'язання: Запишемо рівняння заданого еліпса в параметричному вигляді: x=2*cos(t), y=3*sin(t).

Наведемо графічно траєкторію матеріальної точки вздовж еліпса.

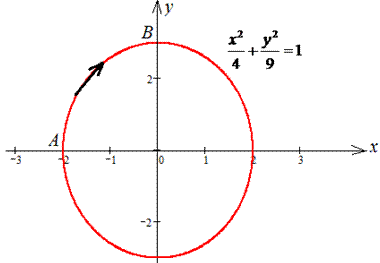
Тоді диференціал змінних за параметром буде рівний dx=-2*sin(t)dt, dy=3*cos(t)dt .
При цьому межі інтегрування обмежаться точками Pi і Pi/2.
Знайдемо роботу сили F по кривій C через криволінійний інтеграл ІІ роду: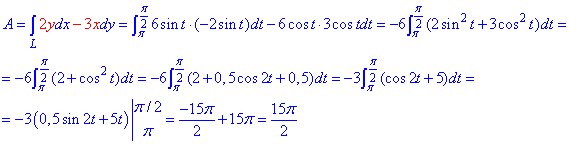
Перегляньте уважно формули інтегрування синуса та косинуса, та пониження степеня для таких функцій.

ЗАВДАННЯ 4.4 Знайти роботу сили 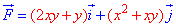при переміщенні вздовж кривої C: y=4-2x^2 від точки 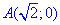до точки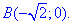
Розв'язання: Побудуємо траєкторію руху матеріальної точки вздовж параболи L: y=4-2x².

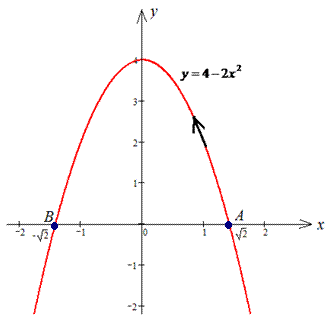
Обчислюємо диференціал дуги y=4-2x², dy=-4x*dx та з умови межі інтегралу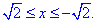
Робота сили F знаходимо за допомогою криволінійного інтеграла ІІ роду

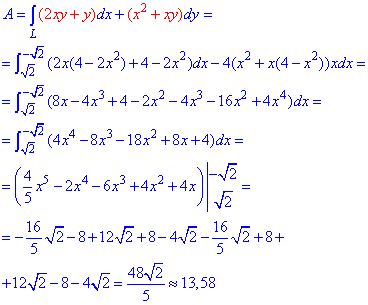
Інтегрування займає не мало часу і при перетвореннях можна допустити помилку, тому будьте уважні в цих моментах.

ЗАВДАННЯ 4.11 Знайти роботу сили 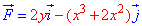при переміщенні вздовж кривої C: y=ln(x) від точки A(1;0) до точки B(e;1).
Розв'язання: Траєкторія матеріальної точки вздовж логарифма має вигляд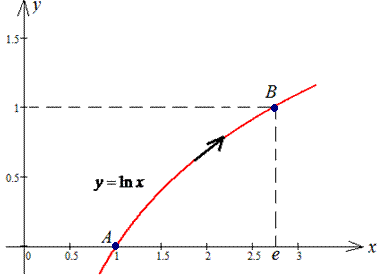

Знаходимо диференціал логарифма y=ln(x), dy=dx/x.
Межі інтегрування змінюються від одиниці до експоненти.
Робота сили F за допомогою криволінійного інтеграла ІІ роду прийме значення:

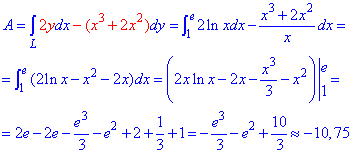
Тут для логарифма застосували правило інтегрування частинами (u*dv).

ЗАВДАННЯ 4.13 Знайти роботу сили F при переміщенні вздовж кривої C: x²+y²=9 від точки A(0;-3) до точки 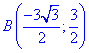, де F задана формулою
.

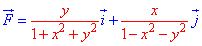Розв'язання: Побудуємо траєкторію руху матеріальної точки вздовж кола радіусом 3.


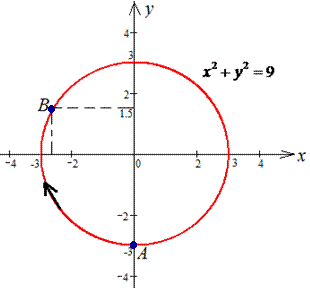
Щоб не виражати дві функції (верхня і нижня крива кола) запишемо залежність x(y) та обчислимо диференціал дуги

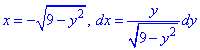
При цьому ордината змінюється від -3 до 3/2.
Застосовуючи криволінійний інтеграл ІІ роду знаходимо роботу сили F при переміщенні вздовж кола:

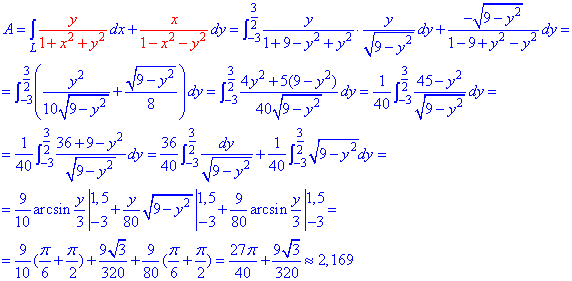
Боротися з коренями під час інтегрування непросто, про що свідчить наведені обчислення.
Набагато простіше обчислювати інтеграл при переході до полярної системи координат.
Далі наведемо методику інтегрування:

ІІ – спосіб:
Запараметризуємо задане коло:

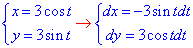
Враховуючи, що під час руху від точки A(0;-3) до точки 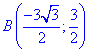кут змінюється від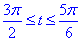
Обчислюємо шуканий криволінійний інтеграл ІІ роду: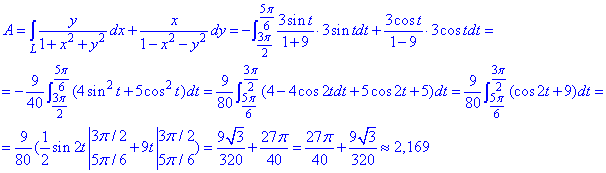
В плані обчислень другий метод легший, тому для кругових та еліптичних форм кривої при симетричному входженні x,y в рівняння сили рекомендуємо переходити до полярної системи координат.

ЗАВДАННЯ 4.15 Знайти роботу сили 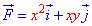при переміщенні вздовж кривої C: 4x²+y²=4 від точки A(0;2) до точки B(-1;0).
Розв'язання: Траєкторія руху матеріальної точки по колу наведена нижче

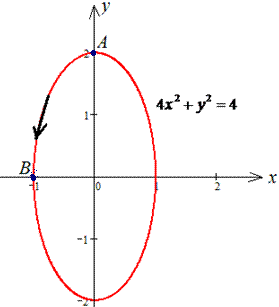
Записуємо верхню дугу еліпса та її похідну. Межі інтегрування змінюються від 0 до -1

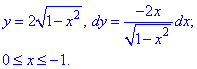
Робота сили F через криволінійний інтеграл ІІ роду виражається залежністю:

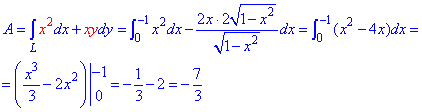
ЗАВДАННЯ 4.18 Знайти роботу сили 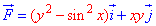при переміщенні вздовж кривої C: y=cos(x) від точки A(Pi/2;0) до точки B(-Pi/2;0).
Розв'язання: Зобразимо траєкторію матеріальної точки вздовж косинуса

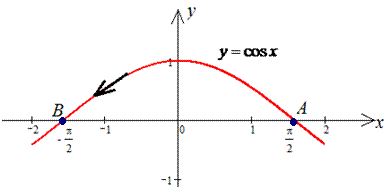
Побудуємо диференціал кривої y=cos(x), dy=-sin(x)*dx.
Він потрібний для зведення криволінійного інтегралу ІІ роду до визначеного.
Знаходимо роботу сили F при переміщенні вздовж контуру

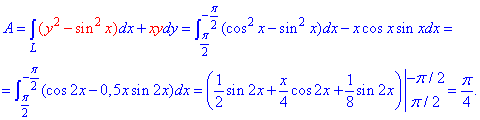
Для пониження під інтегралом степенів косинуса та синуса застосували відомі тригонометричні формули.

ЗАВДАННЯ 4.21 Знайти роботу сили 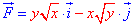при переміщенні вздовж кривої C: y=x³ від точки A(0;0) до точки B(2;8).
Розв'язання: Побудуємо траєкторію матеріальної точки вздовж кривої y=x³.

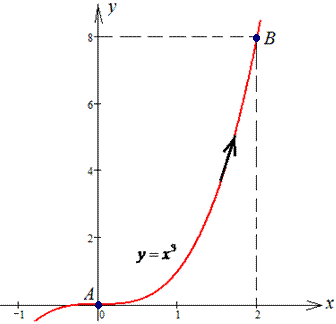
Обчислюємо диференціал дуги dy=3x²dx.
Межі інтегрування наведені на рисунку та в умові.
Робота сили F знаходимо за допомогою криволінійного інтегралу ІІ роду:

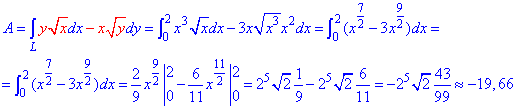
Перетворюємо все до показникової форми та інтегруємо.

ЗАВДАННЯ 4.23 Знайти роботу сили 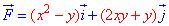при переміщенні вздовж кривої C: x²+2y²=2 від точки 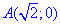до точки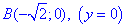
Розв'язання: За інструкцією будуємо траєкторію матеріальної точки вздовж еліпса: x²+2y²=2.

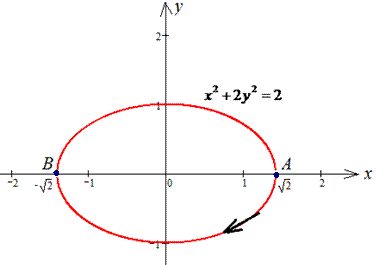
Для простоти обчислень криволінійного інтегралу ІІ роду запараметризуємо еліпс:
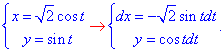, тоді.
Враховуючи, що від точки 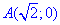до точки 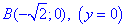кут змінюється за правилом 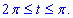переходимо до інтегрування

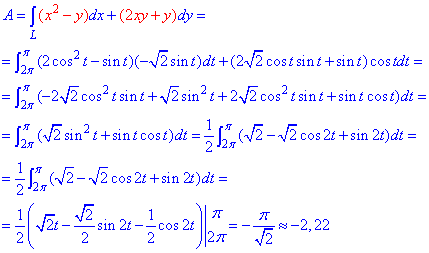
Понижуємо степені та інтегруємо.

ЗАВДАННЯ 4.24 Знайти роботу сили 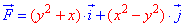при переміщенні вздовж кривої C: y=1-|x| від точки A(-1;0) до точки B(2;-1).
Розв'язання: Наведемо траєкторію матеріальної точки вздовж модуль функції.

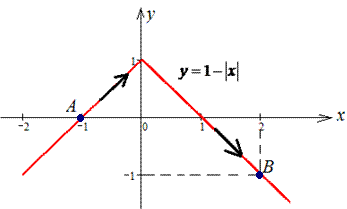
Як не хотілося зустріти завдання з розбиттям кривої на два інтервали, проте одне завдання містить таку умову. Розділимо на дві частини: y=1+x, тоді межі рівні [-1;0] і диференціал dy=dx;
На другій ділянці y=1-x маємо [0;2] і dy=-dx.
Обчислюємо роботу сили F , потрачену на переміщенні точки вздовж модуль функції:

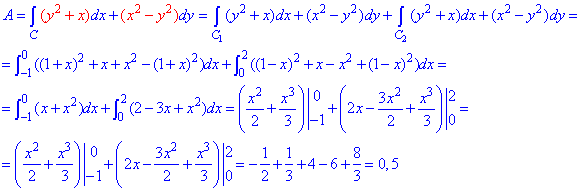
На цьому ознайомлення з такого сорту прикладами завершено. Більше готових відповідей з курсу вищої математики шукайте на сторінках порталу.