На попередніх уроках розібрали готові приклади на паралельне перенесення та симетрію для точок та прямих. З цього та наступного уроку Ви дізнаєтеся, як виконувати самостійно завдання на геометричні перетворення для кіл, парабол, трикутників,
+ навчитеся, як обчислити гомотетію?
Правила виділені в поясненнях необхідно запам'ятати, вони слугують інструкціями до розв'язування відповідних задач на симетрію та паралельний перенос фігур.
Тема: Перетворення фігур
Приклад 43.3 Яка з указаних фігур має центр симетрії?
А | Б | В | Г | Д |
Трапеція | трикутник | кут | промінь | відрізок |
Розв'язування: Фігуру називають центрально-симетричною, якщо існує точка O, при симетрії відносно якої фігура переходить у себе. У трапеції, трикутника, кута, променя немає такої точки, при симетрії відносно якої ці фігури переходили у самих себе. Це випливає згідно з означення цих фігур.
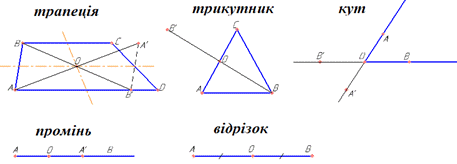
Відрізок – це частина прямої, множина точок якої лежать між двома іншими точками, які називаються кінцями відрізка. Середина цього відрізка є центром симетрії цієї фігури, оскільки всі точки цього відрізка є попарно симетричними відносно середини відрізка.
Серед наведених фігур немає кола, але Ви повинні знати, що коло має безліч осей симетрії, які проходять через центр кола.
Відповідь: відрізок – Д.
Приклад 43.18 Вказати рівняння образу кола (x-1)^2+(y+2)^2=4 при гомотетії з коефіцієнтом 3 і центром у початку координат.
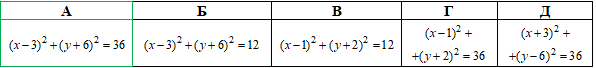
Розв'язування: Гомотетія є перетворенням подібності. На координатній площині гомотетія з центром у початку координат (точка O(0;0)) задається формулами:
{x'=k•x;
y'=k•y},
де (x;y) – координати точки A,
а(x';y') – координати образу цієї точки при гомотетії.
За умовою маємо рівняння кола (x-1)2+(y+2)2=4, у якого S(1;-2) – координати центра кола та |OS|=r=2 – радіус.
За формулами гомотетії знайдемо координати образу кола, де k=3 – коефіцієнт гомотетії (за умовою):
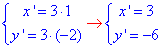
отже отримали точку S'(3;-6).
Радіус образу кола також збільшиться у k=3 разів при гомотетії з центром у початку координат, тобто
|OS'|=3•|OS|=3r=6.
Запишемо рівняння отриманого образу кола:
(x-3)2+(y+6)2=62,
або (x-3)2+(y+6)2=36.
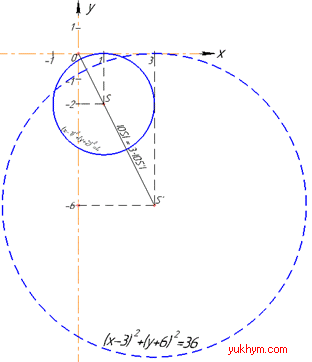
На рисунку при додатному коефцієнті гомотетії k=3>0 точки S(1;-2) і S'(3;-6) лежать по один бік від центра гомотетії (точки O(0;0)).
Відповідь: (x-3)2+(y+6)2=36 – А.
На ЗНО тестах такі завдання не рідкість, тому запам'ятайте схему обчислень.
Приклад 43.25 Дано коло (x-3)2+(y+5)2=4. Установити відповідність між перетвореннями (1–4) та рівняннями образів кола (А–Д).
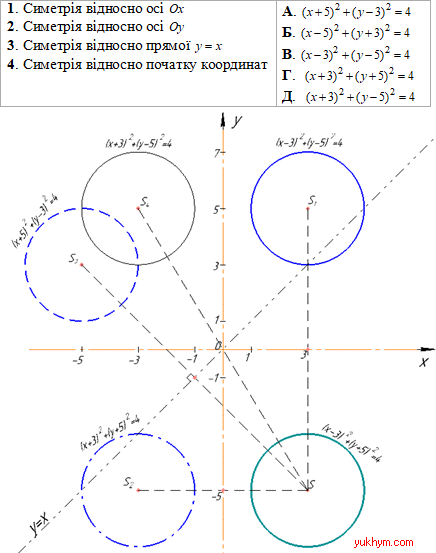
Розв'язування: Маємо коло (x-3)2+(y+5)2=4 з центром у точці S(3;-5) і радіусом r=2. Оскільки при симетрії відносно прямої та відносно точки відстань між точками не змінюється, то r=2 для всіх образів кіл.
Для кожного перетворення (симетрії) знайдемо координати точки образів кіл Sn(x’;y’) та запишемо рівняння образів заданого кола
(x-x’)2+(y-y’)2=4.
1. За властивістю симетрії відносно вісі Ox:
точки, симетричні відносно осі Ox, мають однакові абсциси та протилежні ординати.
Тому при симетрії відносно вісі Ox точка (3;-5) переходить в точку S1(3;5), звідси (x-3)2+(y-5)2=4 – рівняння образу заданого кола.
Відрізок SS1⊥Ox і в точці (3;0) (точка перетину) ділиться . В.
2. За властивістю симетрії відносно вісі Oy:
точки, симетричні відносно осі Oy, мають однакові ординати та протилежні абсциси.
Тому при симетрії відносно вісі Oy точка S(3;-5) переходить в точку S2(-3;-5), звідси (x+3)2+(y+5)2=4 – рівняння образу заданого кола.
Відрізок SS2⊥Oy і в точці (0;-5) (точка перетину) ділиться навпіл. Г.
3. За властивістю симетрії відносно прямої y=x:
у точках, симетричних відносно прямої y=x, ординати та абсциси змінюються місцями.
При симетрії відносно прямої y=x точка S(3;-5) переходить в точку S3(-5;3), звідси (x+3)2+(y-3)2=4 – рівняння образу заданого кола.
Відрізок SS3 перпендикулярний до прямої y=x і в точці (-1;1) (точка перетину) ділиться навпіл. А.
4. За властивістю симетрії відносно початку координат (точки O(0;0)):
якщо початок координат (точка O(0;0) ) є центром симетрії деяких інших точок, то їх відповідні координати мають лише протилежні знаки.
При симетрії відносно початку координат точка S(3;-5) переходить в точку S4(-3;5), звідси (x+3)2+(y-5)2=4 – рівняння образу заданого кола.
Початок координат (точка O(0;0)) є серединою відрізка SS4. Д.
Приклад 43.27 Дано коло (x+3)2+(y-4)2=9. Установити відповідність між гомотетіями (1–4) та рівняннями образів кола (А–Д).
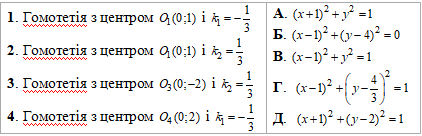
Розв'язування: Маємо коло (x+3)^2+(y-4)^2=9 з центром у точці S(-3;4) і радіусом r=3. Для відшукання образів кіл при заданих гомотетій потрібно знайти координати центрів цих кіл Sn(x’;y’), а довжину радіуса змінити у |k| разів, тобто r’=|k|•r.
Гомотетія є перетворенням подібності. На координатній площині гомотетія з центром у початку координат задається формулами:
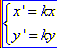
де (x;y) – координати точки S,
k – коефіцієнт гомотетії,
Sn(x’;y’) – координати образу цієї точки при гомотетії, On(x0;y0) – координати центра гомотетії.
Знайдемо рівняння образів кіл (x-x’)2+(y-y’)2=(r’)^2 при кожній гомотетії. Оскільки для кожної заданої гомотетії |k|=1/3, то маємо r’=1/3•3=1.
1. S(-3;4), гомотетія з центром O1(0;1) і k1=-1/3:
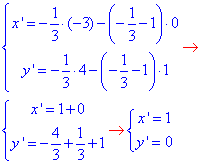
звідси S1(1;0).
Рівняння кола при гомотетії:
(x-1)^2+y^2=1.
На рисунку |O1S1|=1/3•|O1S| і при k<0 точки S(-3;4) і S1(1;0) лежать по різні боки від центра гомотетії (точки O1(0;1)). В.
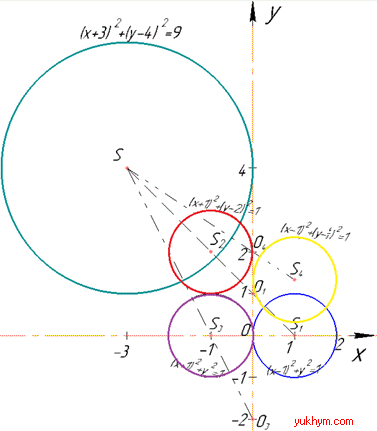
2. S(-3;4), гомотетія з центром O1(0;1) і k2=1/3:
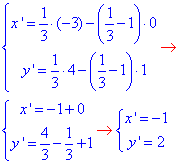
звідси S2(-1;2).
Рівняння образу кола:
(x+1)^2+(y-2)^2=1.
На рисунку образу кіл |O1S2|=1/3•|O1S| та при коефіцієнті гомотетії k>0 точки S(-3;4) і S2(-1;2) лежать по один бік від центра гомотетії (точки O1(0;1)). Д.
3. S(-3;4), гомотетія з центром O3(0;-2) та коефіцієнтом гомотетії k2=1/3:
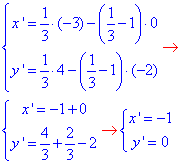
отримали S3(-1;0).
Рівняння образу кола при гомотетії:
(x+1)2+y2=1.
На рисунку |O3S3|=1/3•|O3S| і при k>0 точки S(-3;4) і S3(-1;0) лежать по один бік від центра гомотетії (точки O3(0;-2)). А.
4. S(-3;4), гомотетія з центром O4(0;2) і k1=-1/3:
звідси S4(1;4/3).
Рівняння образу кола:
(x-1)2+(y-4/3)2=1.
На рисунку |O4S4|=1/3•|O4S| і при коефцієнті гомотетії k<0 точки S(-3;4) і S4(1;4/3) лежать по різні боки від центра гомотетії (точки O4(0;2)). Г.
Уважно перегляньте алгоритм обчислення образів кіл за заданими гомотетіями, запам'ятайте, що і для чого виконували. Для засвоєння матеріалу самостійно розв'яжіть кілька однотипних завдань.
Далі розберемо приклади на перетворення подібності для парабол та трикутників.


