Сьогодні розглянемо задачі на властивості прямокутників. Далі задачі на робм, паралелограм, трапеції.
За кілька уроків на 29 прикладах Ви зможете пригадати шкільну практику з геометрії за 8,9 класи.
Прості пояснення та рисунки допоможуть зрозуміти хід обчислень, та швидко підготуватися до ЗНО тестів з математики.
Автори: Анатолій Капіносов, Галина Білоусова, Галина Гап'юк, Сергій Мартинюк, Лариса Олійник, Петро Ульшин, Олег Чиж
Завантажити онлайн відповіді (Посібник для підготовки до зовнішнього незалежного тестування з математики).
Зміст: Посібник містить поради щодо проходження ЗНО з математики та взірці тестових завдань.
Усі задачі однієї теми розміщені в порядку складності.
Рекомендуємо всім завантажити відповіді до ЗНО та самостійно пройти теми, з якими маєте труднощі на практичних.
Тема 32. Чотирикутники
Задачі на прямокутники
У збірнику наведено 29 прикладів з умовами на прямокутники, паралелограми, ромби трапеції. В такому порядку ми їх погрупували, підготували та рекомендуємо до перегляду.
Приклад 32.4 У чотирикутнику діагоналі дорівнюють 8 см і 5 см.
Обчислити периметр чотирикутника, вершинами якого є середини сторін даного чотирикутника.
Обчислення: Завдання не зовсім стосується прямокутників, однак ми його включили оскільки подібне завдання може чекати Вас на тестах, екзаменах чи контрольній роботі.
Нехай маємо чотирикутник ABCD, у якого AC=5 см і BD=8 см – діагоналі.
KLMN – чотирикутник, вершини якого є, відповідно, середини сторін AB, BC, CD і AD чотирикутника ABCD.
Наголошуємо Вам на необхідності робити схематичні рисунки до більшості задач з геометрії.
Як вчать викладачі: гарно виконаний рисунок містить половину розв'язаної задачі.
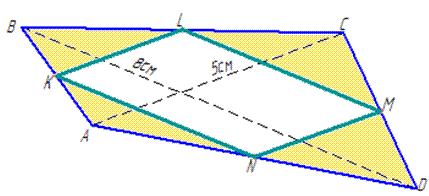
Розглянемо трикутник ABD, у якого KN сполучає середини сторін AB і AD.
Звідси слідує, що KN – середня лінія трикутника ABD.
Тому, за властивістю середньої лінії трикутника ABD:
KN||BD і KN=BD/2=8/2=4 см.
Розглянемо трикутник BCD, у якого LM сполучає середини сторін BC і CD. Звідси слідує, що LM – середня лінія трикутника BCD.
Тому, за властивістю середньої лінії трикутника BCD:
LM||BD і LM=BD/2=4 см.
За теоремою про паралельні прямі («якщо дві прямі паралельні третій, то вони паралельні одна одній») отримаємо, що KN||LM.
Аналогічно встановлюємо, що KL=MN=AC/2=5/2=2,5 см і KL||MN (тобто KL і MN – середні лінії трикутників ABC і ACD, відповідно).
Оскільки у чотирикутника KLMN протилежні сторони паралельні (і рівні), то цей чотирикутник – паралелограм.
Обчислимо його периметр:
P=KL+LM+MN+KN=2(KL+LM)=2(4+2,5)=13 см.
Відповідь: 13 см – Б.
Приклад 32.5 Одна зі сторін прямокутника дорівнює 8 см.
Знайти площу прямокутника, якщо площа круга, описаного навколо нього, дорівнює 25π см^2.
Обчислення: Записуємо все, що нам відомо про прямокутник ABCD, BC=AD=8 см і AB=CD.
За властивістю: діагоналі прямокутника рівні.
Кожна діагональ прямокутника розбиває його на два рівні прямокутні трикутники (ознака рівності: «за трьома сторонами»).
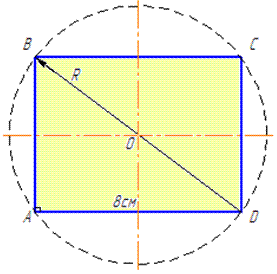
Діагональ прямокутника є гіпотенузою прямокутного трикутника. Оскільки коло описане навколо прямокутника, то ці два рівні прямокутні трикутники вписані у коло. За властивістю: гіпотенуза прямокутного трикутника, вписаного в коло є діаметром цього кола. Звідси слідує, що діагональ прямокутника BD вписаного в коло є діаметром кола 2R (BD=2R).
Площа кола:
S=πR2, де R – радіус описаного навколо прямокутника кола.
Звідси:
25π=πR^2, R^2=25, тому R=5 см.
Отже, BD=2•R=10 см.
Розглянемо прямокутний трикутник ABD (∠BAD=90).
За теоремою Піфагора знайдемо катет AB
(BD=10 см – гіпотенуза, AD=8 см – катет):
BD^2=AB^2+AD^2, звідси сторона рівна
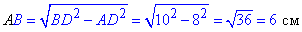
Знайдемо площу прямокутника зі сторонами AD=8 см і AB=6 см:
SABCD=AB•AD=6•8=48 см2.
Відповідь: 48 см^2 – Б.
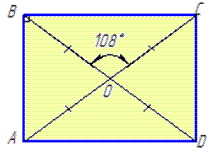
Приклад 32.6 У прямокутнику ABCD точка O – точка перетину діагоналей, ∠BOC=108.
Знайти ∠ABD.
Обчислення: Нехай маємо прямокутник ABCD, AC=BD – діагоналі, ∠BOC=108, де O – точка перетину діагоналей AC і BD.
Оскільки будь-який прямокутник – це паралелограм, то за властивістю:
AO=CO і BO=DO. А так як, за властивістю, у прямокутника діагоналі рівні, то AO=CO=BO=DO.
Розглянемо трикутник BOC, у якого ∠BOC=108 і BO=CO.
Звідси слідує, що трикутник BOC – рівнобедрений з основою BC і бічними сторонами BO, CO.
Тому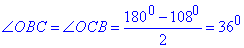 
(за теоремою про суму кутів трикутника).
Оскільки BO є половина діагоналі BD, то ∠DBC=∠OBC=36.
У прямокутника ABCD маємо:
∠DBC+∠ABD=90, звідси слідує, що
∠ABD=90-∠DBC=90-36=54.
Відповідь: 540 – Г.
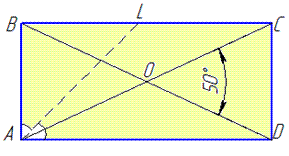
Приклад 32.14 Діагоналі прямокутника утворюють кут 500.
Знайти кут між діагоналлю прямокутника та бісектрисою кута, проведеними з однієї вершини.
Обчислення: У прямокутнику маємо наступні позначення: AC=BD – діагоналі, ∠COD=50, де O – точка перетину діагоналей AC і BD.
Оскільки будь-який прямокутник – це паралелограм, то за властивістю маємо:
AO=CO і BO=DO.
А так як, за властивістю, у прямокутника діагоналі рівні, то AO=CO=BO=DO.
Знайдемо ∠AOD за теоремою про суму суміжних кутів ∠COD і ∠AOD:
∠COD+∠AOD=180, звідси ∠AOD=180-∠COD=180-50=130.
Розглянемо трикутник AOD.
У нього ∠AOD=130 і AO=DO.
Звідси слідує, що трикутник AOD – рівнобедрений з основою AD, тому ∠CAD=∠OAD як кути при основі AD рівнобедреного трикутника AOD.
За теоремою про суму кутів трикутника знайдемо кути при основі AD трикутника AOD:
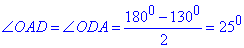
звідси ∠CAD=∠OAD=25.
Оскільки AL – бісектриса кута A, а ∠A=90 (за означенням прямокутника), то
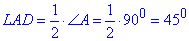
Знайдемо ∠LAC – кут між бісектрисою AL і діагоналлю AC прямокутника ABCD, які проведені з кута A:
∠LAC=∠LAD-∠CAD=45-25=20, отже ∠LAC=20.
Відповідь: 200 – Д.
Приклад 32.29 Перпендикуляр, проведений з вершини прямокутника на діагональ, дорівнює 12 і поділяє діагональ на відрізки, різниця яких дорівнює 7.
Знайти площу прямокутника.
Обчислення: Задано прямокутник ABCD, AC– діагональ, BH⊥AD, BH=12.
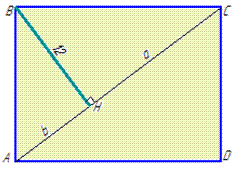
Введемо позначення: AH=b і HC=a, (тут AC=a+b), тоді за умовою задачі a-b=7 (*).
І – спосіб (важчий!):
Із прямокутного трикутника ABH (∠AHB=90) запишемо гіпотенузу AB:
AB^2=AH^2+BH^2, звідси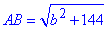 
Із прямокутного трикутника BCH (∠BHC=90) запишемо гіпотенузу BC:
BC^2=HC^2+BH^2, звідси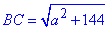 
Площу прямокутника можна обчислити:
1) за двома її сторонами, тобто S[ABCD]=AB•BC, тобто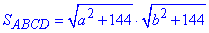 
2) як суму площ прямокутних трикутників ABC і ADC.
Оскільки протилежні сторони прямокутника рівні (за властивістю), то ΔABC=ΔADC, звідси
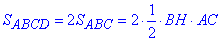
звідси S[ABCD]=12(a+b).
Прирівняємо отримані вирази для обчислення площі прямокутника ABCD:
(**).
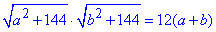Отримали два рівняння (*) і (**) з двома невідомими a і b:
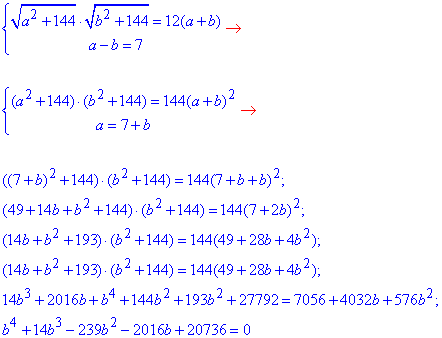
b1=b2=-16<0 (не задовольняє умові задачі), b3=b4=9.
Отже, b=9 і a=16.
Звідси AC=16+9=25.
Обчислимо площу прямокутника ABCD:
S[ABCD]=12•25=300.
ІІ – спосіб (легший!):
Обчислення: Нехай нам відомо наступне:
∠BAH=alpha, тоді ∠BAH=90-alpha (∠AHB=90 за умовою задачі).
Оскільки ∠ABC=90 (за означенням прямокутника ABCD), то
∠CBH=90-∠ABH=90-(90-alpha)=alpha.
Отже , ∠BAH=∠CBH.
Розглянемо два прямокутні трикутники ABH і BCH зі спільним катетом BH=12.
Оскільки ∠BAH=∠CBH, то звідси випливає, що ці трикутники подібні (ознака подібності : «за рівним гострим кутом»).
Тому маємо
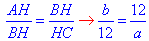
a•b=12•12=144 (**).
Отримали два рівняння (*) і (**) з двома невідомими a і b:
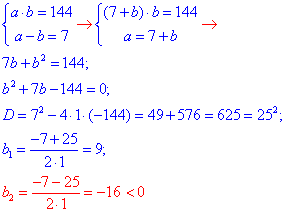
Другий корінь квадратного рівняння не задовольняє умові задачі.
Отже, b=9 і a=16.
Звідси AC=9+16=25.
Обчислимо площу прямокутника:
S[ABCD]=12(a+b)=12•25=300.
Відповідь: 300.
Приклад 32.47 Скільки потрібно листів бляхи завширшки 3 м, щоб обгородити земельну ділянку прямокутної форми під будівництво офісного центру, площа якої дорівнює 480 м2, а одна зі сторін – 16 м?
Розв'язування: Зробимо математичну модель задачі. Офісну ділянку замінимо на прямокутник ABCD, у якого AB=CD=16 м, BC=AD - сторони і SABCD=480 м2 - площа.
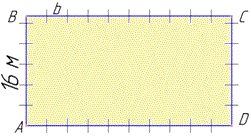
Знайдемо іншу сторону прямокутника ABCD:
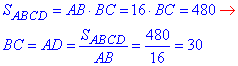
Обчислимо периметр (суму всіх довжин сторін) прямокутника ABCD:
PABCD=2(AB+BC)=2(16+30)=92 (м).
Кількість листків бляхи, щоб обгородити земельну ділянку, визначають як відношення периметра ділянки до ширини одного листка.
За умовою: b=3 м - ширина одного листка бляхи, звідси отримаємо
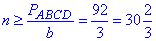
найменше натуральне значення що задовільняє нерівність n=31.
Відповідь: 31.
Ось такого типу завдання Вас чекатимуть на зовнішньому незалежному оцінюванні і їх Ви повинні вміти обчислювати, інакше не наберете потрібних балів для вступу у ВУЗ.
Тож вчіться, працюйте багато самостійно і з часом будете вільно використовувати усі властивості чотирикутників.
