Площа поверхні правильної чотирикутної призми рівна сумі двох площ основ та 4 поверхонь бічних граней прямокутників (1).
Формули площі поверхні правильної чотирикутної призми

Якщо врахувати, що в основі правильної чотирикутної призми маємо квадрат, то площа основи рівна
Sосн=a*a=a2.
Якщо висота призми рівна h, то площа однієї бічної грані рівна:
Sб.г.=a*h.
При підставленні у формулу (1) повної площі призми дістанемо (2, 3) формулу:
Sпризми=2a2+4a*h.
Оскільки в перерізах маємо або квадрат або прямокутники, то прямих задач на повну поверхню призми не так і багато, та й хід їх обчислень простий. Більший інтерес представляє на практиці обчислення площі поверхні правильної чотирикутної призми вписаної в кулю чи циліндр, такі завдання дал розберемо.
Приклад 1. Сторона основи правильної чотирикутної призми дорівнює 3 см, а її висота - 7 см. Знайдіть площу бічної поверхні призми та її об'єм.
Розв'язування: За формулою (2) обчислюємо площу бічної поверхні:
Sб.п.=2a2+4a*h=2*3*3+4*3*7=102 см2.
Об'єм призми рівний добутку площі основи на висоту призми:
V=a2*h=3*3*7=9*7=63 см3.
Відповідь: Sб.п.=102 см2, об'єм призми 63 см3.
Такі завдання можна розв'язувати в 6-7 класі, проте завдання на діагоналі, застосування теореми Піфагора вимагають більших знань і часто не під силу учням 9-11 класів.
Перегляньте та самостійно проаналізуйте схеми обчислення наступних задач з геометрії.
Приклад 2. Сторона основи правильної чотирикутної призми дорівнює 4 см, а її висота - 8 см. Знайдіть площу перерізу призми, який проходить через діагональ основи паралельно діагоналі призми.
Розв'язування: Можлив два варіанти, розглянемо обидва (див. рисунок). 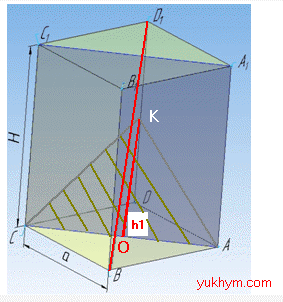
Перший - простий випадок, коли діагональ основи та діагональ призми виходять з однієї з її вершин (C). Тоді перерізом призми буде прямокутник, що проходить через діагональ основи та два ребра призми.
Довжина діагоналі основи рівна
CA=√(42+42)=4√2 см.
Площа перерізу призми рівна добутку діагоналі основи на висоту:
S=CA*H=4√2*8=32√2 см2.
ІІ випадок.
Площина паралельна діагоналі призми BD1, але виходить з діагоналі основи CA.
Тоді перерізом буде рівнобедрений трикутник ΔCKA, основа якого вже знайдена:
CA=4√2 см.
Оскільки площина паралельна діагоналі призми, то
DK=DD1/2=8/2=4 см.
Тоді сторону трикутника KA знайдемо з ΔADK в якого KD=AD=4 см:
KA=√(42+42)=4√2 см.
Обчислимо висоту h1 трикутника ΔCKA за теоремою Піфагора:
h1=√(KA2-OA2)
OA=CA/2=2√2 см;
h1=√(16-8) =2√2 см.
Знаходимо площу шуканого перерізу через півдобуток основи трикутника (діагоналі основи призми) на висоту трикутника
S=CA*h1=4√2*2√2=16 см2.
Обидві відповіді правильні.
Приклад 3. В циліндр, радіус основи якого дорівнює 2√2см, а висота 5 см, вписано правильну чотирикутну призму. Знайти площу повної поверхні цієї призми.
Розв'язування:Побудуємо правильну призму вписану в циліндр.
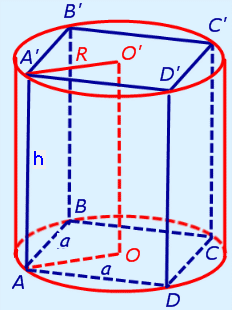
За умовою AO=2√2 см, h=5 см.
Діагональ квадрата в основі
d=2*AO=4√2 см.
Довжина діагоналі через сторону квадрата
d=a√2, прирівняємо з попереднім записом
a√2=4√2,
a=4 см.
Площа повної поверхні призми рівна сумі площ 2 основ (квадратів) + 4 поверхні ребер (прямокутників).
Sосн=а²=4²=16;
Р=4а=4*4=16;
Sбіч.п.=Р*h=16*5=80;
Sп.п.=2Sосн+Sбіч.п.=2*16+80=112 см2.
Відповідь: площа повної поверхні призми = 112 см2.
Приклад 4. Правильну чотирикутну призму вписали у циліндр із радіусом основи 4 см і висотою 7√2 см. Знайдіть площу бічної поверхні призми.
Розв'язування: Побудуємо допоміжний рисунок до задачі.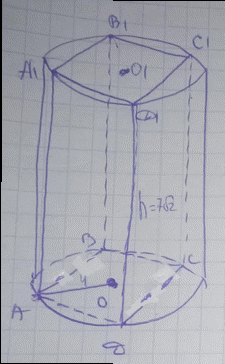
Оскільки призма правильна, то радіус циліндра рівний половині діагоналі квадрата в основі призми
R=AO=AC/2 .
Сторона квадрата (за теоремою Піфагора):
AB=AD=4√2 см.
Площа бічної поверхні призми рівна добутку периметру квадрата на висоту:
P=4*AB=4*4√2=16√2 см.
S=P*h=16√2*7√2=224 см2.
Відповідь: 224 см2.
Приклад 5. У кулю радіуса R вписано правильну чотирикутну призму, Діагональ якої нахилена до площини основи під кутом альфа. Знайдіть сторону основи призми.
Розв'язування: Побудуємо призму вписану в кулю до задачі:
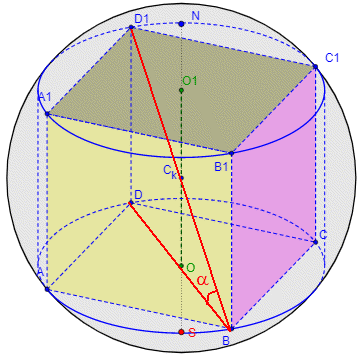
В основі – квадрат зі стороною а.
Діагональ призми D1B=2R, квадрату – DB=d,
α - кут між діагоналлю призми та діагоналлю основи (квадрата).
Виразимо діагональ квадрату через діагональ призми:
d=2R*cosα;
та через сторону квадрата
d=a√2.
Прирівняємо та знайдемо сторону основи
a√2=2R*cosα;
a=d/√2=2Rcosα/√2=√2*R*cosα.
Відповідь: a=√2*R*cosα.
Приклад 6. Діагональний переріз правильної чотирикутної призми є квадратом з площею 4n^2 см2. Знайдіть сторону основи.
Розв'язування: Підказкою до задачі є умова, що переріз BB1D1D є квадратом, тому висота призми рівна діагоналі основи BD:
H=BB1=BD.
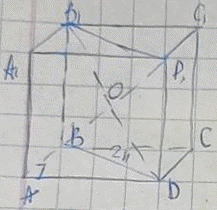
Випишемо формулу площі перерізу та обчислимо BD:
S=BB1*BD=4n^2 см2;
S=BD2=4n2=(2n)2;
BD=2n см.
За теоремою Піфагора діагональ основи (квадрата) рівна:
BD=√(AB2+AD)=AD√2.
Прирівнюємо до попередньо виведеного значення:
AD√2=2n см;
AD=2n/√2=√2n см.
От і всі розрахунки до задачі.
Відповідь: сторона основи = √2n см.
Приклад 7. Діагональ правильної чотирикутної призми утворює з площиною бічної грані кут 30 градусів. Знайдіть:
1) кут між діагоналлю призми та площиною основи;
2) площу бічної поверхні призми, якщо довжина сторони основи рівна 6 см.
Розв'язування: Кут між прямою та площиною – це кут між прямою і проекцією прямої на площину. Побудуємо рисунок призми:
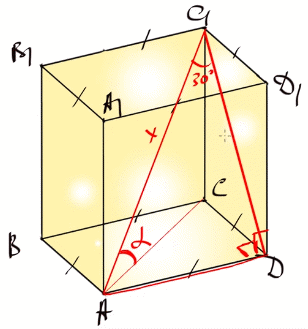
Оскільки проекцією діагоналі AC1 на бічну поверхню CDD1C1 є діагональ бічної грані C1D, то вказаний в умові кут це ∠AC1D=300.
∠ADC1=900, оскільки основа і бічні грані попарно перпендикулярні.
Кут між діагоналлю та основою – це кут ∠CAC1. Його потрібно знайти
Позначимо через х – діагональ призми.
Тоді катет AD навпроти кута 300 рівний половині гіпотенузи AC1=x,
AD=x/2.
CD=AD=x/2 - сторона квадрата основи.
За теоремою Піфагора обчислимо діагональ квадрата:
AС=x/2√(1+1)=x√2/2.
В прямокутному трикутнику ΔACC1 катет і гіпотенуза пов'язані косинусом:
cosα=AC/AC1=x√2/2:x=√2/2,
звідси α=450.
Потрібний кут ми знайшли.
Обчислимо площу бічної поверхні призми, знаючи кут α=450.
Тоді висота призми рівна діагоналі основи (як сторони рівнобедреного трикутника):
h=AC=6√2 см.
Периметр основи рівний
P=4a=4*6=24 см.
Площа бічної поверхні призми:
Sб.п.=P*h=24*6√2=144√2 см2
Відповідь:144√2 см2.
Приклад 8. Знайдіть площу діагонального перерізу, площу бічної поверхні та площу основи правильної чотирикутної призми, у якої діагональ призми дорівнює d, діагональ бічної грані нахилена до площини основи під кутом alpha.
Розв'язування: Виконаємо допоміжний рисунок.
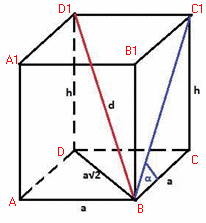
Призма правильна, тому в основі маємо квадрат.
Нехай сторона квадрату рівна "а". Тоді діагональ квадрату рівна a√2.
Виразимо висоту призми H через кут нахилу діагоналі на боковій грані
H=a•tg(α).
Квадрат діагоналі призми
d²=H²+2a².
(з прямокутного трикутника діагонального перерізу).
d²=a²•tg²α+2a²=a²(2+tgα).
Виразимо основу через діагональ призми
a=d/√(2+tgα).
Підставимо в формулу висоти призми:
h=a•tgα=d•tgα/√(2+tgα).
Тоді площа діагонального перерізу рівна:
Sд.п.=a√2•h=
= d√2/√(2+tgα)•dtgα/√(2+tgα)=
=d²•tgα•√2/(2+tgα). (1)
Площа бічної поверхні рівна добутку периметру основи на висоту призми:
Sб.п.=4•a•h=
=4d/(√((2+tgα))•d•tgα/(√((2+tgα))=
= 4d²•tgα/(2+tgα). (2)
Площа основи (квадрата) рівна квадрату сторони:
Soсн=a²=d²/(2+tgα). (3)
Тільки що вивели формули площ поверхонь правильної чотирикутної призми через її діагональ і кут діагоналі до основи на ребрі призми.
Відповідь: 1. площа діагонального перерізу - Sд.п.=d²•tgα•√2/(2+tgα).
2. площа бічної поверхні - Sб.п.=4d²•tgα/(2+tgα).
3. площа основи - Soсн=d²/(2+tgα).
Діліться посиланнями на кращі задачі з друзями та пам'ятайте, що тут Ви можете переглянути безліч готових завдань зі шкільної практики, готові відповіді до ЗНО підготовки та матеріали перших курсів у ВУЗах.


