підручник для 11 класу:
Збірник задач та контрольних робіт
Автор: А. Г. Мерзляк, В. Б. Полонський, Ю.М. Рабінович, М. С. Якір
Мова: Українська мова
Видавництво: Гімназія
Рік: 2011
ISBN: 978-966-474-163-4
Завантажити (скачать) ГДЗ: Алгебра 11 клас Мерзляк. Збірник задач і контрольних робіт. Формат: PDF
Зміст: Посібник містить близько 700 задач з алгебри. Складається з двох варіантів "Тренувальних вправ" по 239 завдань у кожному на різні теми та контрольних робіт для перевірки закріпленого матеріалу.
-------------------------------------------
1 Варіант
Приклад 230. Знайдіть площу фігури, обмеженої:
1) параболою у=6-х^2 і прямою у=2;
Розв'язання:
Спочатку знаходимо точки перетину кривих
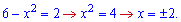
Від верхньої кривої віднімаємо нижню та обчислюємо площу інтегруванням
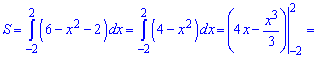
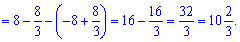
2) параболою у=4-х^2 і прямою у=х+2;
Розв'язання:
Знаходимо точки перетину параболи із прямою
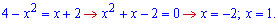
Обчислюємо площу заштрихованої фігури
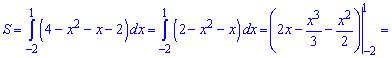
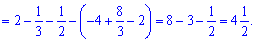
3) параболою у=-х^2-4х, прямою у=4 і віссю ординат;
Розв'язання:
Знаходимо перетин кривих
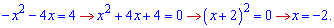
Оскільки пряма знаходиться вище параболи, то від неї віднімаємо рівняння параболи і інтегруємо
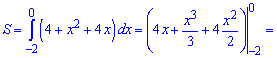
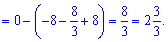
4) параболою у=х^2-6х+9 і прямою у=-х+5;
Розв'язання:
Точки перетину знаходимо з рівняння
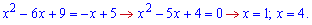
Пряма між заданими точками проходить вище на графіку, тому від неї віднімаємо рівняння параболи і інтегруємо у знайдених межах. В результаті площа буде рівна
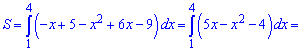
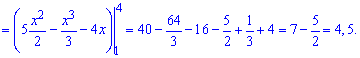
5) графіками функцій у=sqrt(x) та у=x/3;
Розв'язання:
Точки перетину кривих
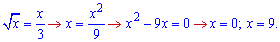
Площу знаходимо інтегруванням різниці кривих
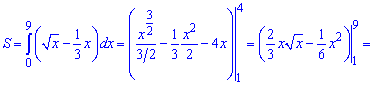
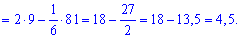
6) параболою у=x^2+2х+2 і прямою у=2х+3;
Розв'язання:
Знаходимо точки перетину
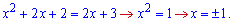
Обчислюємо площу фігури між кривими
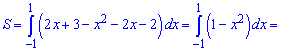
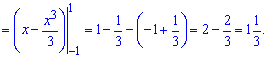
7) параболами у=-х^2+2х+1 та у=х^2-4х+5;
Розв'язання:
Знайдемо точки перетину парабол
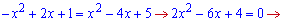
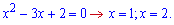
Підставляємо границі інтегрування та обчислюємо площу
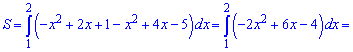
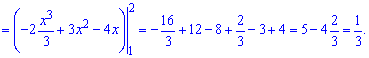
8) графіками функцій у=sqrt(x+2) та у=0,5x+1;
Розв'язання:
Запишемо рівняння прямої у вигляді
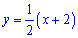
та знайдемо точки перетину з кореневою функцією
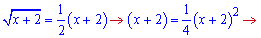
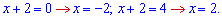
Підставимо межі інтегрування та знайдемо площу
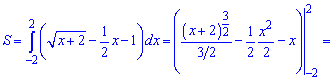
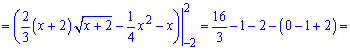
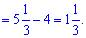
9) графіком функції у=еxp^(-x) і прямими у=1, x=-3;
Розв'язання:
Знайдемо точку перетину
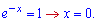
Від експоненти віднімаємо пряму та обчислюємо площу
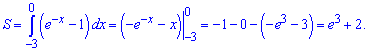
10) графіком функції у=2^х і прямими х=0, у=4;
Розв'язання:
Обчислимо точку перетину із степеневого рівняння
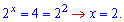
Визначимо площу інтегруванням
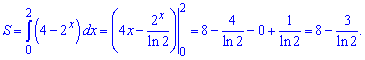
11) графіками функцій у=4^x-1, у=7–4^x і прямою x=0;
Розв'язання:
Обчислимо точку перетину двох графіків функцій
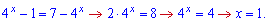
Підставляємо межі інтегрування та знаходимо площу
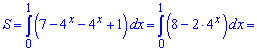
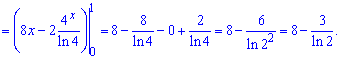
12) графіками рівнянь xy=6, x^2-5x+6=0 і у=0;
Розв'язання:
За теоремою Вієта знаходимо корені квадратного рівняння
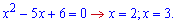
З першої функції виражаємо змінну y
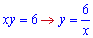
та підставимо в інтеграл
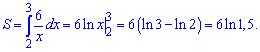
13) графіком функції у=4/x і прямими x=1, у=2;
Розв'язання:
Знаходимо точку перетину кривих
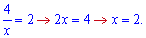
Від верхньої кривої віднімаємо нижню та підставляємо у формулу площі
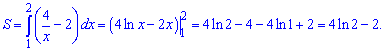
14) графіком функції у=5/x і прямими у=5, х=5;
Розв'язання:
Встановимо точку перетину з рівняння
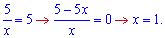
Для відшукання площі інтегруємо різницю кривих у відповідному інтервалі
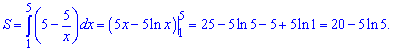
15) графіком функції у=7/x і прямою х+у=8;
Розв'язання:
Схема обчислень попередня – знаходимо точки перетину кривих

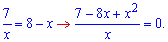
Квадратне рівняння в чисельнику розв'яжемо за теоремою Вієта
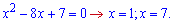
Площу фігури знаходимо інтегруванням
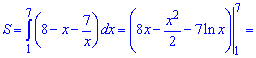
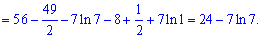
16) графіком функції y=2/x і прямими у=х-1, х=3;
Розв'язання:
Другу межу інтегрування знаходимо з рівняння
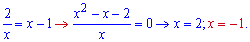
Одну точку відкидаємо, вона лежить лівіше критичної точки (0). Обчислюємо площу фігури
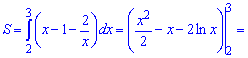
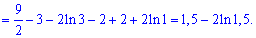
17) графіками функцій у=х^4, у=1/x і прямою х=2;
Розв'язання:
Знаходимо межу інтегрування
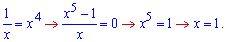
Інтегруванням знаходимо площу
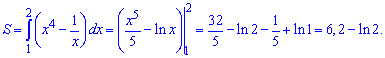
18) графіками функцій у=sqrt(x), у =1/x і прямою х=4;
Розв'язання:
Знаходимо перетин кривих
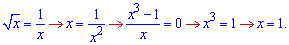
Площа між кривими рівна інтегралу
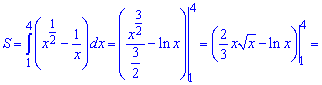
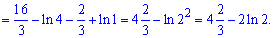
19) графіком функції у =3/(x-2) і прямими х=4, х=6.
Розв'язання:
Оскільки межі інтегрування задані, то для знаходження площі обчислюємо інтеграл
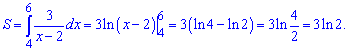
-------------------------------------------------------------
Розв'язки до Збірника задач з алгебри 11 клас. Мерзляк
- Попередні відповіді - Площа криволінійної трапеції
- Наступні відповіді - Площа криволінійної трапеції. №231-233
- Зміст: ГДЗ Алгебра 11 клас Мерзляк
Переглянути тематично подібні матеріали
Сподобався матеріал - порекомендуйте друзям!



