підручник для 11 класу:
Збірник задач та контрольних робіт
Автор: А. Г. Мерзляк, В. Б. Полонський, Ю.М. Рабінович, М. С. Якір
Мова: Українська мова
Видавництво: Гімназія
Рік: 2011
ISBN: 978-966-474-163-4
Завантажити (скачать) ГДЗ: Алгебра 11 клас Мерзляк. Збірник задач і контрольних робіт. Формат: PDF
Зміст: Посібник містить близько 700 задач з алгебри. Складається з двох варіантів "Тренувальних вправ" по 239 завдань у кожному на різні теми та контрольних робіт для перевірки закріпленого матеріалу.
-------------------------------------------
1 Варіант
Приклад 227. Знайдіть площу фігури, обмеженої:
1) параболою у=х^2 та прямими у=0, x=-2 і х=-1;
Розв'язання:
Площу криволінійної трапеції обчислюємо інтегруванням
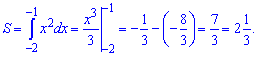
2) графіком функції у =х^3 та прямими у=0 і х=1;
Розв'язання:
Інтеграл від нуля до одиниці рівний
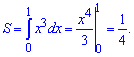
3) графіком функції у=cos(x) та прямими у=0, х=-Pi/2 і x=Pi/6;
Розв'язання:
Знаходимо інтеграл від косинуса і підставляємо межі
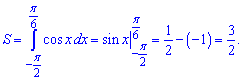
4) параболою у = 4-х^2 і віссю абсцис;
Розв'язання:
Знаходимо точки перетину параболи і абсцис
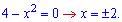
Знайдені точки і будуть межами інтегрування
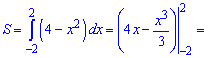
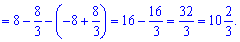
5) параболою у=x^2-2x віссю абсцис і прямою x=4;
Розв'язання:
Знаходимо точки перетину параболи і осі абсцис
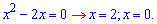
Виконаємо побудову функції Площа складатиметься з двох доданків, причому слід пам'ятати, що площа величина додатна.
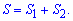
Для відшукання підінтегральної функції від верхньої кривої слід відняти нижню В нашому випадку отримаємо
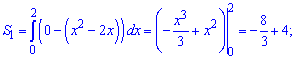
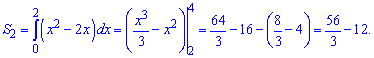
Сумуємо знайдені площі
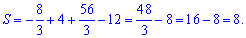
6) графіком функції у=sqrt(x) та прямими у=0, х=1 і х=9;
Розв'язання:
Виконуємо необхідні обчислення
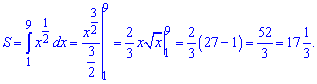
7) графіком функції у=sqrt(x-3) та прямими у=0 і x=7;
Розв'язання:
Знаходимо точки перетину кореня і осі абсцис
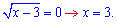
Інтегруємо кореневу функцію між 3 і 7
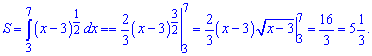
8) графіком функції у=sin(2x) та прямими у=0, x=Pi/8 і x=3Pi/8;
Розв'язання:
Інтегруємо синус подвійного кута у вказаних межах
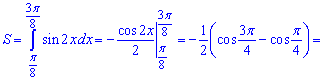
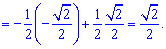
9) графіком функції у=3^x та прямими у=0, x=-1 і x=1;
Розв'язання:
Показникова функція матиме наступний вигляд. Знаходимо площу криволінійної трапеції
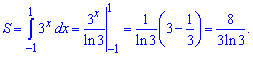
10) графіком функції у=exp^(3x-2) та прямими у=0, x= 0 і х=1;
Розв'язання:
Інтегруємо експоненту
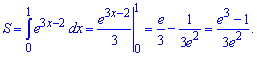
11) графіком функції у=1/x та прямими у=0, x=1 і x=4.
Розв'язання:
Знаходимо площу інтегруванням
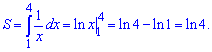
Приклад 228. Доведіть, що площі криволінійних трапецій, заштрихованих на рисунку 2, рівні.
Розв'язання:
Шукані площі рівні інтегралам
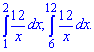
Обчислюємо інтеграли та перевіряємо чи вони рівні між собою.
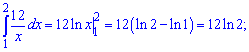
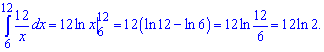
Рівність площ доведено.
Приклад 229. Обчисліть площу заштрихованої фігури, зображеної на рисунку 3.
Розв'язання:
Для обчислення площі від верхньої кривої віднімаємо нижню та інтегруємо між точками, де вони перетинаються
а) 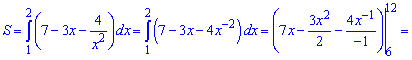
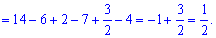
б) 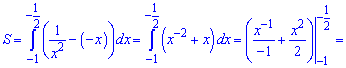
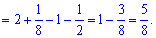
в) 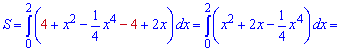
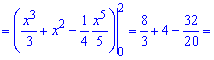
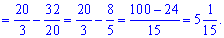
г) 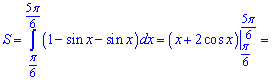
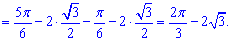
д) 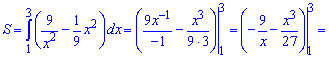
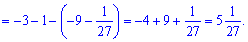
-------------------------------------------------------------
Розв'язки до Збірника задач з алгебри 11 клас. Мерзляк
- Попередні відповіді - Інтеграл. Формула Ньютона-Лейбніца. № 224-226
- Наступні відповіді - Площа криволінійної трапеції. №230
- Зміст: ГДЗ Алгебра 11 клас Мерзляк
Переглянути тематично подібні матеріали
Сподобався матеріал - порекомендуйте друзям!



