підручник для 11 класу:
Збірник задач та контрольних робіт
Автор: А. Г. Мерзляк, В. Б. Полонський, Ю.М. Рабінович, М. С. Якір
Мова: Українська мова
Видавництво: Гімназія
Рік: 2011
ISBN: 978-966-474-163-4
Завантажити (скачать) ГДЗ: Алгебра 11 клас Мерзляк. Збірник задач і контрольних робіт. Формат: PDF
Зміст: Посібник містить близько 700 задач з алгебри. Складається з двох варіантів "Тренувальних вправ" по 239 завдань у кожному на різні теми та контрольних робіт для перевірки закріпленого матеріалу.
-------------------------------------------
1 Варіант
Приклад 231. Знайдіть площу фігури, обмеженої:
1) графіками функцій у=sqrt(x+1) і у=sqrt(7-x) та віссю абсцис;
Розв'язання:
Приклади такого роду розв'язують сумуванням двох інтегралів. Потрібно знайти перетин кривих з віссю абсцис та між собою. Знайдені точки і будуть межами інтегруванням при розбитті площі фігури на дві. Виконаємо вказані операції до завдання
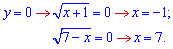

При відомих межах інтегрування обчислення площі зводиться до сумування інтегралів
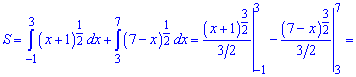
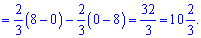
2) графіком функції
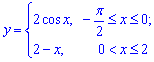
та віссю абсцис;
Розв'язання:
Задана функція складається з двох частин. Підставляємо межі та знаходимо площу
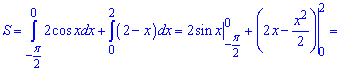
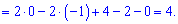
3) графіками функцій у=sqrt(x), у=2x/3-2/3 та віссю абсцис.
Розв'язання:
Виконуємо згідно інструкції першого завдання: Точки перетину з віссю абсцис
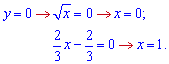
перетин графіків між собою
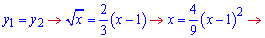
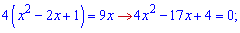
Обчислюємо дискримінант
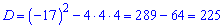
та корені рівняння
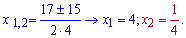
Оскільки точка перетину функцій не лежить між точками перетину графіків з віссю абсцис то площа буде рівна сумі інтегралів
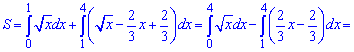
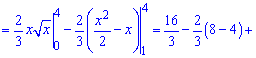
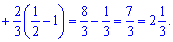
Приклад 232. Використовуючи геометричний зміст інтегралу, обчисліть:
1) 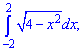
Розв'язання:
Запишемо підінтегральну функцію у вигляді
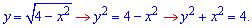
Це рівняння кола з радіусом R=2. Його площа рівна –
S=Pi*R^2=4Pi.
Оскільки заданий інтеграл рівний половині кола, то його площа рівна
S1=2Pi.
2) 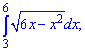
Розв'язання:
Виконаємо подібні перетворення з підінтегральною функцією
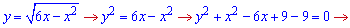
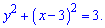
Викладки я думаю Вам зрозумілі. Ми звели функцію до рівняння кола з радіусом R=3 та центром в точці (3;0). Його площа рівна
S=Pi*R^2=9Pi.
Значення інтегралу рівне одній четвертій круга, тобто
S1=9Pi/4.
3) 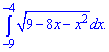
Розв'язання:
Зведемо функцію до канонічного вигляду
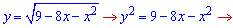
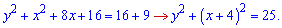
Отримали рівняння кола з центром у (-4;0) та радіусом R=5. Інтеграл рівний четвертині площі круга, тобто
S1=Pi*5^2/4=25Pi/4.
Приклад 233. Знайдіть площу фігури, обмеженої параболою у=3x-x^2, дотичною, проведеною до даної параболи в точці з абсцисою x0=3 і віссю ординат.
Розв'язання:
Завдання на перший погляд складне, однак виконавши всі дії по черзі під силу кожному школяру. Побудуємо рівняння дотичної. Знаходимо похідну функції
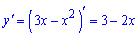
Підстановкою точки визначимо кутовий коефіцієнт дотичної
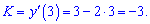
Рівняння дотичної набуде вигляду
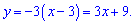
Вісь ординат відповідає межі інтегрування x=0. Від прямої віднімаємо рівняння параболи та інтегруванням знаходимо площу
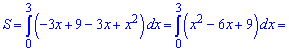
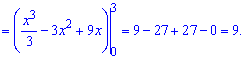
-------------------------------------------------------------
Розв'язки до Збірника задач з алгебри 11 клас. Мерзляк
- Попередні відповіді - Площа криволінійної трапеції. №230
- Наступні відповіді - Площа криволінійної трапеції. №234-237
- Зміст: ГДЗ Алгебра 11 клас Мерзляк
Переглянути тематично подібні матеріали
Сподобався матеріал - порекомендуйте друзям!



