Аналіз курсової роботи з математичного аналізу «Функції багатьох змінних» містить найпоширеніші завдання, які Вас можуть чекати в навчанні. Розбирайте відповіді до завдань та вивчайте методики обчислень.
Завдання 1 Визначити і зобразити область визначення функції
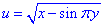
Розв'язання:Маємо кореневу фунцію від x-sin(Pi*y), підкореневий вираз повинен бути більший рівний нуля. Звідси маємо нерівність
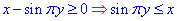
яка виконується при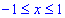 
, оскільки синус не може приймати значень поза цим діапазоном.
Беручи обернену функцію - арксинус, отримаємо
(*)
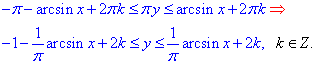Запишемо область визначення заданої функції для деяких значень k:
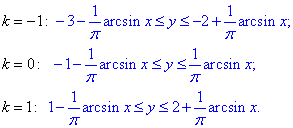
Насправді ж k належить множині ціих чисель, для цих значень знаходили, щоб побудувати область визначення, а також встановити її періодичність.
Графік області визначення має вигляд
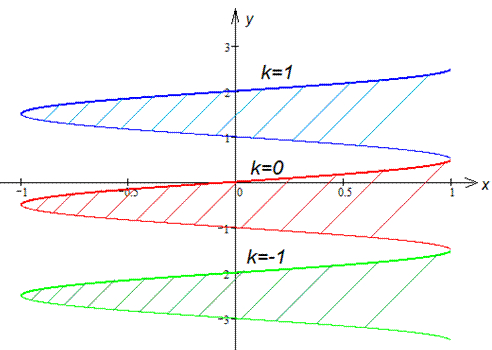
При x>1 функція визначена всюди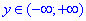 
, при x<-1 маємо порожню множину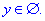 
Між цими двома точками область визначення обмежена періодичним арксинусом, закон якого задається рівнянням (*).
Завдання 2 Побудувати лінії рівня функції u=x/|x+y|.
Розв'язання: Сукупність точок області D, в яких функція u=f(x,y) має постійне значення u(x;y)=c утворює деяку лінію. Якщо візьмемо інше значення c, то отримаємо іншу лінію. Ці лінії називаються лініями рівня.
В залежності від знаку модуля в знаменнику функцію двох змінних можна розписати наступним чином:
а) для x>-y отримаємо:
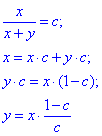
б) для x<-y будемо мати:
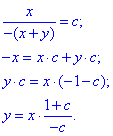
З першого рівняння c=1 при y>0;
З другого c=-1 при y<0;
c=0 при x=0 і абсцисі відмінній від нуля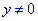 
.
Графік ліній рівня можна подати у вигляді пучка прямих
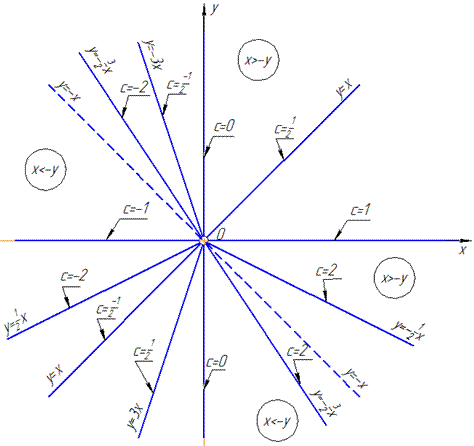
Точка (0;0) вирізана, тому кожна пряма в нулі має розрив.
Завдання 3 Знайти повторні границі
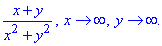
Розв'язання: Під повторними мають на увазі границі по першій змінній коли друга вважається сталою, а далі визначення по другій при змінній прямуючій до свого значення. В заданому варіанті обидві змінні прямують до безмежності, тому границі можемо розписати наступним чином.
а)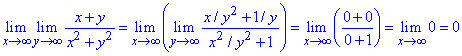 
б)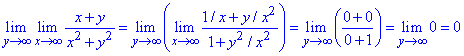 
Якщо не знаєте, як знайти границю в безмежності, то почитайте методику обчислення границь, там все детально пояснено.
А ми переходимо до пояснень наступного прикладу.
Завдання 4 Дослідити функцію u(x,y) на рівномірну неперервність на множині E:
u(x;y)=x2-y,
.
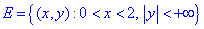Розв'язання: За теоремою про рівномірну неперервність, для довільного як завгодно малого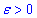 
і будь-яких двох точок з множини
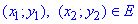
повинна вионуватися умова
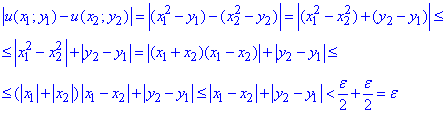
Звідси маємо, як тільки прирости менші половини "епсилон" умова
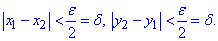
виконується.
Звідси, за означенням, функція u(x,y) рівномірно-неперервна на множині E.
Завдання 5 Знайти часткові похідні першого і другого порядку функції u(x,y)=x*sin(y2)
Розв'язання: Знаходимо часткові похідні першого порядку:
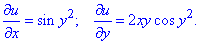
Маючи перші похідні обчислюємо часткові похідні другого порядку:
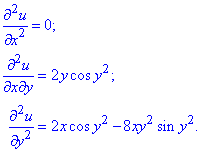
Обчислення не складні, кому важко почитайте уроки знаходження похідних.
Завдання 6 Знайти часткові похідні першого і другого порядку функції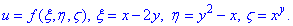 
Розв'язання: Маємо параметрично задану функцію, аргументи якої є в свою чергу функціями 'x,y'. В цьому випадку потрібно шукати похідну по параметру, а далі похідну параметра за x чи y.
Формули дещо скадніші порівняно з попереднім завданням, однак часткові похідні першого порядку беруться легко:
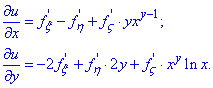
Що стосується часткових похідних другого порядку, то тут головне не пропустити жодного з доданків та взяти за усіма параметрами та змінними. Так знаходимо другу похідну за змінною x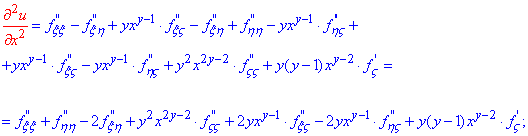
другу часткову похідну зазмінною y
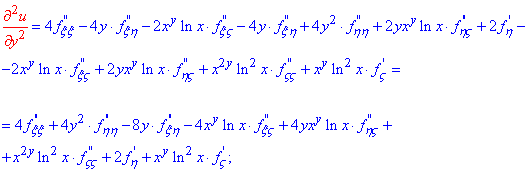
та мішану похідну
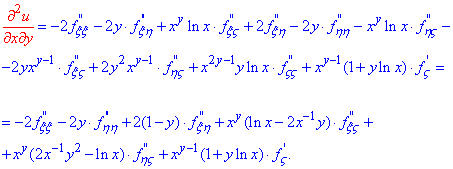
Формули важкі для читання, проте на практиці бувають і важчі функції декількох змінних.
Завдання 7 Знайти вказану часткову похідну функції u=x9*ln(1+y)
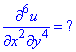
Розв'язання: Тут потрібно знайти мішану похідну 6 порядку, двічі по x, а потім від знайденого виразу 4 похідну по y.
Побудуємо рекурентні формули, врахувавши що змінні входять в функцію роздільно.
Для будь-якого порядку часткової похідної за змінною y отримаємо залежності
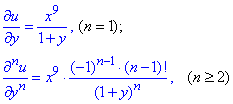
За змінною x диференціювати не проблема, тому можемо записати шукану часткову похідну
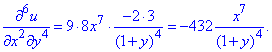
Послідовно знаходження похідної 6 порядку зайняло б чимало часу, і навіть в цьому випадку на певній ітерації Ви змоги побачити певну закономірність при знаходженні похідної за y.
Завдання 8 Записати перший диференціал функції трьох змінних
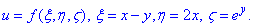
Розв'язання: За правилами диференціювання параметрично заданих функцій отримаємо
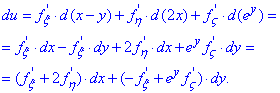
Тут формула достатньо добре описує усі правила, то ж подібне завдання Ви зможете виконати самостійо.
Завдання 9 Записати диференціали першого і другого порядку
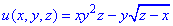
Розв'язання: Маємо функцію трьох змінних, диференціюємо кожен доданок за трьома змінними та групуємо при відповідних диференціалах
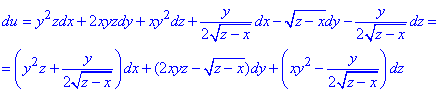
Ось так легко отримали диференціал першого порядку.
Далі отриманий вираз повторно диференціюємо та згруповуємо подібні доданки.
В результаті отримаємо
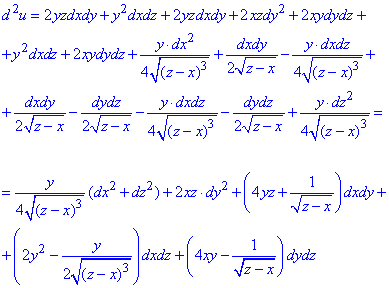
На цьому завдання розв'язано.
Завдання 10Записати диференціали першого і другого порядку параметричної функції
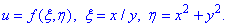
Розв'язання: Якщо попередній приклад для декого з Вас виглядав важким, то диференціал параметрично заданої функції обчислювати куди важче. Слід шукати диференціал функції за параметром, а далі параметра за кожною із змінних. В результаті перший диференціал розписуємо в два рядки
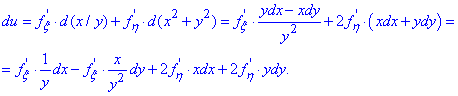
Повторне диференціювання куди важче і тут більша ймовірність допустити помилку, тому не спішіть при розписуванні
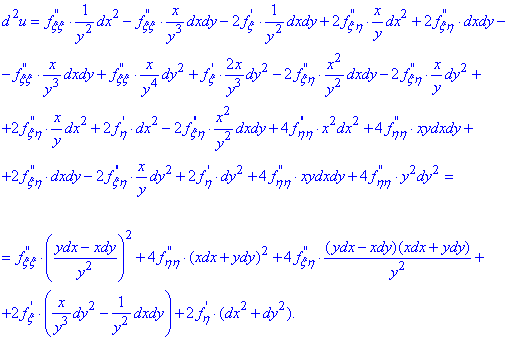
Кінцевий запис можна отримати лише при групуванні множників біля диференціалів за параметром, і то якщо маєте великий досвід чи немалу практичну підготовку.
Завдання 11 Знайти мішану похідну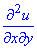 
функції, заданої неявно
.
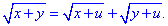Розв'язання: Знайдемо часткові похідні першого порядку - для цього диференціюємо обидві частини за кожною їз змінних, а далі групуємо додани, що містять потрібну похідну.
Спершу знаходимо похдну по x
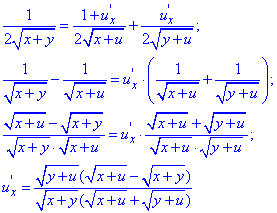
Аналогічно обчислюємо похідну по y
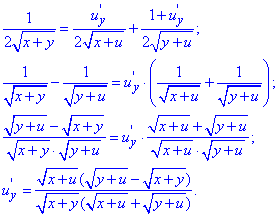
Знайдемо мішану похідну 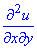другого порядку, для цього похідну за x диференціюємо по y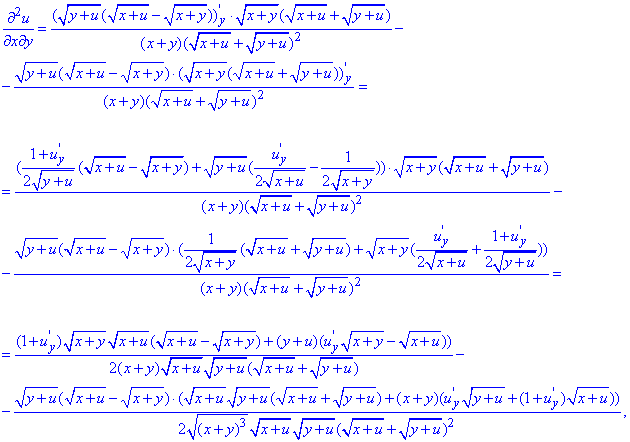
де
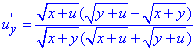
Формули такі громіздкі, тому що маємо похідну від частки функцій + в чисельнику і знаменнику маємо добутки коренів, що в свою чергу теж збільшують кількість доданків.
Все решта зводиться до групування подібних доданків, яке тут не до кінця завершене.
Останній запис можна ще більше спростити, але суть курсової не в цьому.
Тут не вмістилися всі завдання, тому перегляньте наступні розв'язки.
