Метод Лагранжа є ефективним для знаходження умовного екстремуму функції двох z=f(x,y), трьох чи багатьох змінних, особливо коли функцію зв'язку φ(x,y)=0 не можна подати у вигляді явної функції y=φ(x) або x=φ(y).
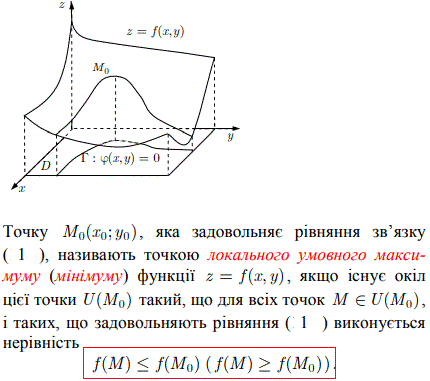
Нехай в області D задано функцію двох змінних f(x,y) і контур Γ, який задано рівнянням φ(x,y)=0 та повністю належить D.
Задача полягає у визначенні на лінії Г точки екстремуму M0(x0;y0), в якій функція f(x,y) досягає максимуму або мінімуму з урахуванням умови φ(x,y)=0.
Вираз φ(x,y)=0 називають рівнянням зв’язку або зв’язком.
За умов зв’язку точка M0(x0;y0) називається точкою локального умовного максимуму [мінімуму] функції z=f(x,y), якщо знайдеться окіл точки U(M0) в якому для всіх точок M∈U(M0) виконується нерівність
f(M)≤ f(M0)
[f(M)≥f(M0)].
Метод Лагранжа знаходження умовного екстремуму для функції двох змінних
Для визначення критичної точки будують функцію Лагранжа та досліджують її.
Функція Лагранжа. Нехай M0(x0;y0) – точка умовного екстремуму.
Необхідні умови умовного екстремуму функції z=f(x,y) при зв’язку φ(x,y)=0.
Складемо допоміжну функцію
L(x,y,λ)= f(x,y)+ λ• φ(x,y), (2)
де λ – деяке поки, що невідоме число.
Залежність L(x,y,λ) називають функцією Лагранжа, а число λ – множником Лагранжа.
Число λ разом з x0 та y0 обчислюють з системи трьох рівнянь = функція зв’язку + два рівняння з часткових похідних f(x,y).
Теорема 1. Необхідні умови умовного екстремуму.
Теорема 2. Достатні умови умовного екстремуму
Виділені в теоремах формули необхідні для обчислення умовного екстремуму та визначення максимум чи мінімум досягається в стаціонарній точці. Більш детально їх розглянемо на готових відповідях до завдань на умовні екстремуми.
Приклади знаходження умовного екстремуму методом Лагранжа
Приклад 5.(417) Знайти екстремум функції z=1/x+1/y, якщо x+y=2.
Розв'язання: Випишемо функцію Лагранжа L(x,y,λ)= 1/x+1/y + λ (x+y-2).
Знайдемо частинні похідні І порядку функції L(x,y,λ):
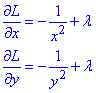
На основі обчислених частинних похідних складаємо систему рівнянь (3) для визначення стаціонарної точки та множника Лагранжа. Третє рівняння це умова зв'язку x+y=2:
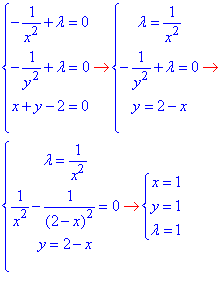
Після розв'язання системи маємо M0(1;1) - стаціонарна точка, тоді z(M0)=1/1+1/1=2.
Множник Лагранжа ніде далі не фігурує, тому на ньому уваги при обчисленнях не акцентують.
Знайдемо часткові похідні ІІ порядку функції Лагранжа L(x,y,λ) в стаціонарній точці:
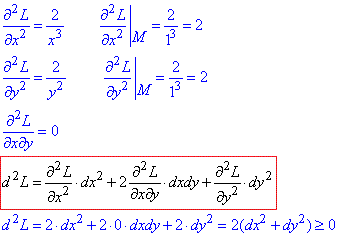
Маємо в дужках квадрати диференціалів, тому d2L≥0. Таким чином, знайдена точка екстремума M0(1;1) є точкою умовного мінімуму функції z=1/x+1/y, а функція в ній приймає zmin=2.
Приклад 6.(418) Для функції двох змінних z=xy знайти умовний екстремум, якщо x+y=1.
Розв'язання: Складаємо функцію Лагранжа
L(x,y,λ)= xy+λ(x+y-1).
Далі від неї обчислюємо частинні похідні І порядку за змінними x та y:
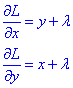
На їх основі складаємо два із трьох рівнянь, додаємо до них рівняння зв'язку x+y-1=0 та розв'язуємо її відносно x,y та множника Лагранжа λ:
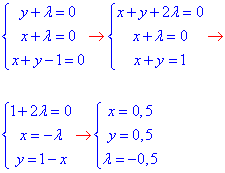
Звідси виписуємо M0(0,5;0,5) - стаціонарну точку та знаходимо значення функції в ній
z(M0)=0,5•0,5=0,25.
Для встановлення знаку другого диференціалу знайдемо частинніі похідні ІІ порядку функції Лагранжа L(x,y,λ) та підставимо у формулу:
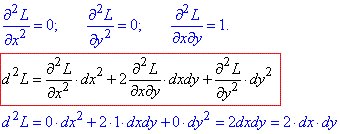
Останній вираз потрібно розписати, тому що для прямої x+y=1, або y=1-x маємо dy=-dx, і відповідно другий диференціал стає від'ємним
d2L=2dx•dy=2dx•d(1-x)=2dx•(-dx)=-2dx2≤0.
Оскільки d2L≤0, то точка M0(0,5;0,5) є точкою умовного максимуму функції z=xy і набуває значення zmax=0,25.
Приклад 7.(419) Для функції трьох змінних u=x+y+z з умовою зв’язку 1/x+1/y+1/z=1 знайти умовний екстремум.
Розв'язання: Складемо функцію Лагранжа
L(x,y,λ)=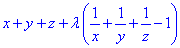 
Знайдемо частинні похідні І порядку функції Лагранжа:
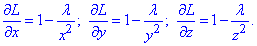
Складаємо систему чотирьох рівнянь відносно координат критичної точки та множника Лагранжа λ:
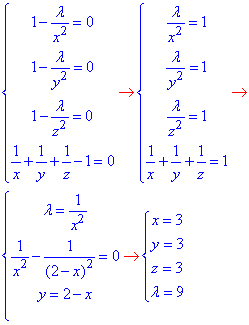
Звідси маємо M(3;3;3) - стаціонарна точка, тоді u(M)=3+3+3=9.
Для визначення чи маємо умовний максимум чи мінімум необхідно визначити знак другого диференціала від функції Лагранжа. Оскільки маємо функцію 3 змінних, то потрібно знайти три частинні похідні другого порядку в стаціонарній точці та три мішані похідні другого порядку.
Далі все це підставляємо у виділену формулу та визначаємо знак d2L:
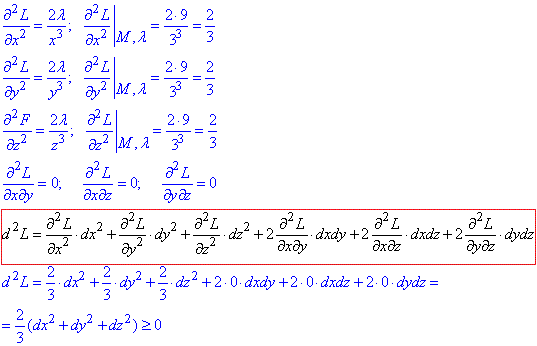
Отримали d2L≥0, отже точка M(3;3;3) є точкою умовного мінімуму функції u=x+y+z, і в ній досягає значення umin=9.
Всі
Приклад 8.(439) Знайти найменшу відстань між параболою y=x^2 і прямою x-y-2=0.
Розв'язання: Відстань від точки M(x;y) до прямої a•x+b•y+c=0 обчислюється за формулою:
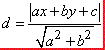
За умовою завдання маємо:
a=1, b=-1 і c=-2;
точка M(x;y) належить параболі y=x2.
Складаємо рівняння відстані
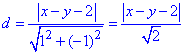
Потрібно знайти екстремум d=|x-y-2|/√2 за умови y=x2.
Функція Лагранжа при цьому прийме вигляд
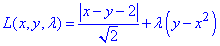
Обчислимо часткові похідні І порядку функції L(x,y,λ):
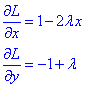
Знайдемо множник Лагранжа та критичні точки з системи рівнянь:
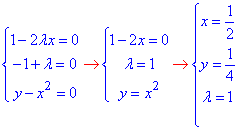
звідси шукана відстань рівна
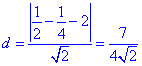
M0(1/2;1/4) - стаціонарна точка.
Знайдемо часткові похідні ІІ порядку функції Лагранжа в стаціонарній точці:
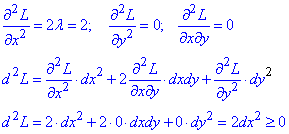
Другий диференціал d2L≥0, тому точка M0(1/2;1/4) є точкою умовного мінімуму функції d=|x-y-2|/√2, тобто dmin=7/(4√2) – найменша відстань від параболи y=x2 до прямої x-y-2=0.
Приклад 9.(440) На параболі x^2+2xy+y2+4y=0 знайти точку, найменш віддалену від прямої 3x-6y+4=0.
Розв'язання: Віддаль від точки M(x;y) до прямої a•x+b•y+c знайдемо за формулою:
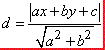
З умови завдання виписуємо сталі: a=3, b=-6 і c=4;
точка M(x;y) належить параболі x2+2xy+y2+4y=0.
Звідси відстань рівна модулю
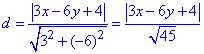
Точка M(x;y) на параболі x2+2xy+y2+4y=0 буде найменш віддаленою від прямої 3x-6y+4=0, якщо виконується умова
|3x-6y+4|→min.
Маємо знайти мінімум функції u=|3x-6y+4| за умови, що точки (x0,y0) належать параболі x2+2xy+y2+4y=0.
Побудуємо функцію Лагранжа L(x,y,λ)= |3x-6y+4|+ λ(x2+2xy+y2+4y).
Знайдемо її частинні похідні І порядку:
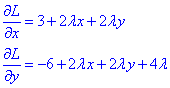
Критичні точки та множник Лагранжа λ знайдемо з системи рівнянь:
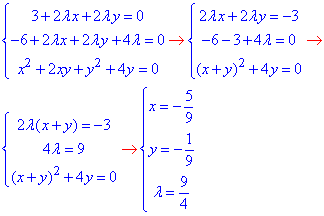
тоді u(M0)=|3x0-6y0+4|=|3•(-5/9)-6•(-1/9)+4|=3.
Cтаціонарна точка має координати M0(-5/9;-1/9).
Знайдемо частинні похідні ІІ порядку функції Лагранжа L(x,y,λ) в стаціонарній точці та підставимо в диференціал 2 порядку:
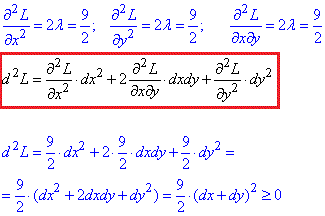
Встановили, що диференціал другого порядку додатний d2L≥0, тому точка M0(-5/9;-1/9) є точкою умовного мінімуму функції u=|3x-6y+4|, тобто на параболі x2+2xy+y2+4y=0 є найменш віддаленою від прямої 3x-6y+4=0.
Відстань від цієї точки до прямої: dmin=u(M0)/√45=1/√5).
Подібних прикладів можна навести ще багато, алгоритм обчислення умовного екстремуму від того не поміняється, і навряд Ви знайдете готову відповідь до завдання, що Вам потрібно. Тому беріть наведену тут методику за інструкцію і самостійно пробуйте знаходити умовний екстремум.
