ЗНО математика. Задачі з планіметрії 1

Шановні школярі, випускники, абітурієнти, цей розділ допоможе підготуватися до зовнішнього оцінювання 2015 року. Відповіді до тестів допоможуть Вам зрозуміти матеріал та методику обчислень при підготовці, систематизувати та підвищити накопичений рівень знань з математики. Рішення прикладів з математики будуть цікаві для школярів 9, 10, 11 класів, а також їх батьків.

Розділ V. Планіметрія

В завданнях 5.33 - 5.45 правильна відповідь оцінюється 2 балами.

Задача 5.39 У трикутнику АВС бісектриси ВD і АЕ внутрішніх кутів В і А перетинаються у точці О. Обчисліть довжину сторони АС, якщо АВ = 12, АО : ОЕ = 3 : 2 та АD:DС=6:7.
Розв'язання: Бісектриса кута трикутника ділить протилежну сторону у відношенні рівному відношенню прилеглих сторін.

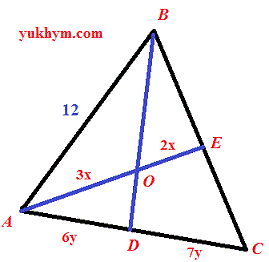
Ця властивість важка для запам'ятовування, проте в задачах на трикутники доволі часто зустрічається. Згідно властивості бісектриси BD отримаємо
AB/BC=6/7.
Звідси знаходимо сторону трикутника
BC=12*7/6=14 (cм).
Таке саму схему застосовуємо і до іншої сторони
AB/BE=3/2.
З відношення знаходимо частину сторони трикутника
AB/BE=3/2,
звідси
ВE=12*2/3=8 (см).
Другий відрізок рівний
14-8=6 (см).
Знаючи ці відрізки складаємо пропорцію для обчислення невідомої сторони трикутника
АВ/АС=BE/EC,
що еквiвалентно
12/AC=8/6;
AC=12*6/8=9 (см).
З цій задачі властивість бісектриси довелось застосувати тричі. Без знання властивості в інший спосіб задачу не розв'язати.
Відповідь: 9.

Задача 5.40 Середня лінія трапеції дорівнює 7, а висота 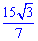Кут між діагоналями трапеції дорівнює 120°. Знайдіть добуток довжин діагоналей трапеції.
Розв'язання: Щоб розв'язати задачу на трапецію необхідно скористатися двома формулами площі. Згідно першої формули площі трапеції вона рівна добутку середньої лінії на висоту.

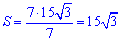
За другою формулою площа рівна добутку діагоналей трапеції на косинус кута між ними.

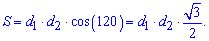
Прирівнявши площі між собою, отримаємо залежність для знаходження добутку довжин діагоналей трапеції
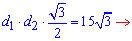
добуток діагоналей
d₁*d₂=15*2=30.
Обчислення як бачите не складні головне знати властивості фігур та необхідні формули.
Відповідь: 30.

Задача 5.41 (Т-06, 7) Обчисліть скалярний добуток векторів, зображених на рисунку.

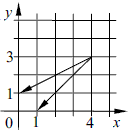
Розв'язання: З побудови знаходимо координати векторів, для цього від кінця вектора віднімаємо координати початку.

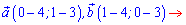
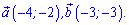
Далі підставляємо значення в формулу скалярного добутку
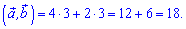
скалярний добуток
В школі подібні завдання на вектори в 8-9 класі проробляють досить часто.
Відповідь: 18.
Допомога з математики у вигляді готових рішень полегшить навчання всіх школярів і буде гарною інструкцією на іспитах і тестах. Готові тестові приклади обов'язково стануть в нагоді у навчанні школярам в 9, 10, 11 класі. Залишайтеся з нами і підготовка до ЗНО з математики залишиться для Вас приємним спогадом та зекономить багато часу та грошей на репетиторів.