ЗНО математика. Задачі на площу фігур

Шановні школярі, випускники, абітурієнти, цей розділ допоможе підготуватися до зовнішнього оцінювання 2017 року. Відповіді до тестів допоможуть Вам зрозуміти матеріал та методику обчислень при підготовці, систематизувати та підвищити накопичений рівень знань з математики. Рішення прикладів з математики будуть цікаві для школярів 9, 10, 11 класів, а також їх батьків.

Розділ V. Планіметрія

В завданнях 5.33 - 5.45 правильна відповідь оцінюється 2 балами.

Задача 5.33 Основи трапеції дорівнюють 11 см і 4 см, а діагоналі 9 см і 12 см. Знайдіть площу трапеції, в см² .

Розв'язання: Спершу виконаємо побудову трапеції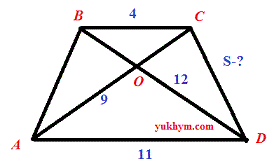
трапеція За властивостями трапеції трикутники, які утворилися перетином діагоналей подібні. Коефіцієнт подібності рівний відношенню основ 4/11. Діагоналі в точці перетину діляться у співвідношенні 4:11 (на 4+11=15 частин).
Знайдемо з пропорцій сторони трикутників
9/15*4=2,4 см;
9/15*11=6,6 см.
12/15*4=3,2 см;
12-3,2=8,8.
Наступним кроком обчислимо площу трикутників зі сторонами 4; 3,2; 2,4 см та 11; 6,6; 8,8 см. За формулою Герона знаходимо площу
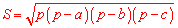
формула Герона
Площа меншого трикутника рівна

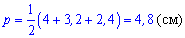
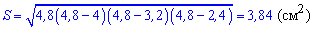
Площа більшого трикутника

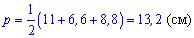
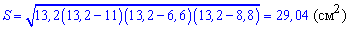
Знаючи площу трикутників і їхні основи з формули
S=1/2*a*h
знаходимо висоту трикутника

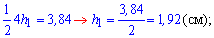
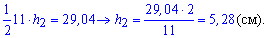
Далі знаходимо висоту трапеції через суму висот трикутників
H=1,92+5,28=7,2 (см).
Обчислюємо площу трапеції
S=(4+11)/2*7,2=54 (сантиметри квадратних).
Обчислення займають багато часу як на тестове завдання + застосування формули Герона зручне при наявності калькулятора. Тому при тестуванні повинен бути простіший спосіб обчислення даної задачі. Хто має ідеї або знає іншу методику обчислень, просимо повідомити в коментарях або надіслати на пошту.
Відповідь: 54.

Задача 5.34 Дано точки А (-8; -2), В (-4; 3) і С (-1; -3). Точка D належить прямій у=4 та 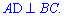Знайдіть координати точки D.
Розв'язання: Оскільки точка D належить прямій у=4, то її координати D(x;4). Обчислимо вектори, на які накладена умова перпендикулярності.

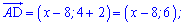
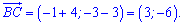
Скалярний добуток перпендикулярних векторів рівний нулю. Звідси складаємо рівняння для знаходження абсциси точки D

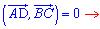
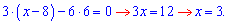
В результаті обчислень отримаємо координати точки D(3;4).
Відповідь: D(3;4).

Задача 5.35 З вершин В і D прямокутника АВСD до діагоналі АС проведені перпендикуляри ВЕ та DF. Відстань між точками Е та F дорівнює 16 см, а ВЕ — 24 см. Обчисліть площу прямокутника у см²
Розв'язання: Виконуємо побудову прямокутника до задачі.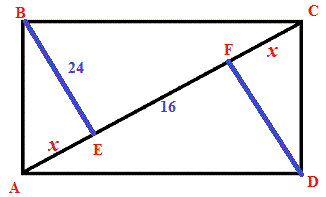

З побудови відомо EF=16 см, BE=24см. Далі потрібно знати правило, що висота проведеного з вершини прямого кута трикутника рівна середньому геометричному відрізків, які відтинає на основі.

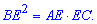
Позначимо AE через х.
Складемо рівняння
24*24=x*(x+16);
x^2+16*x-576=0.
Корені квадратного рівняння рівні x=17,3; x=-33,3.
Один корінь відкидаємо, при другому основа рівна
2*x+16=2*17,3+16=50,6 (см).
Площа прямокутника рівна площі двох трикутників
S=50,6*24=1214,4 (сантиметри квадратні).
В цьому завданні щось не в порядку з умовою, оскільки корені рівняння вийшли ірраціональними, а на тестах таких випадків практично не зустрічається.
Відповідь: 1214,4.

Допомога з математики у вигляді готових рішень полегшить навчання всіх школярів і буде гарною інструкцією на іспитах і тестах. Готові тестові приклади обов'язково стануть в нагоді у навчанні школярам в 9, 10, 11 класі. Залишайтеся з нами і підготовка до ЗНО з математики залишиться для Вас приємним спогадом та зекономить багато часу та грошей на репетиторів.

Відповіді до ЗНО тестів