Шановні школярі, випускники, абітурієнти, цей розділ допоможе підготуватися до зовнішнього оцінювання 2017 року. Відповіді до тестів допоможуть Вам зрозуміти матеріал та методику обчислень, систематизувати та підвищити накопичений рівень знань з математики.
Розділ II. Рівняння і нерівності
Завдання 2.32 (Т-06, 41) Задано 4 рівняння:
1. 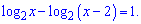
2. 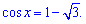
3.|x+2|=-3.
4. 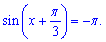
Укажіть рівняння, яке НЕ МАЄ коренів на множині дійсних чисел.
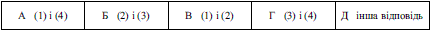
Розв'язання:
1. Почнемо аналіз з логарифмічного рівняння. Його можна переписати у вигляді
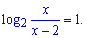
Область допустимих значень x>2. Розв'язок логарифмічного рівняння знаходимо з умови
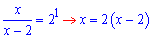
х=2*х-4;
2х-х=4; х=4.
Рівняння має один корінь.
2. Оцінимо праву сторону рівняння, якщо вона за модулем не перевищує одиницю то корінь існує.

Отже косинус такого числа існує.
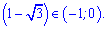 .
.
3. |x+2|=-3 – рівняння з модулем немає коренів, оскільки модуль від'ємним бути не може.
4. По аналогії з косинусом, синус за модулем не повинен перевищувати одиницю.
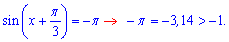
Однак Pi більше за одиницю, отже рівняння не має коренів. Підсумовуючи написане вище 3 і 4 рівняння не мають коренів.
Це відповідає варіанту Г ЗНО тестів.
Відповідь: Г.
В завданнях 2.33 - 2.86 правильна відповідь оцінюється 2 балами.
Завдання 2.33 (Т-06, 26) Розв'яжіть ірраціональне рівняння
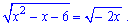
Якщо рівняння має один корінь, запишіть його у відповідь. Якщо рівняння має кілька коренів, запишіть у відповідь їх добуток.
Розв'язання: Починаємо аналіз з ОДЗ коренів:
x2-x-6>0;
-2x>0; x<0.
Рівняння під коренем можна записати у вигляді
(x-3)(x+2).
Остаточно ОДЗ запишемо інтервалом
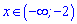 .
.
Підносимо обидві сторони рівняння до квадрату
x2-x-6=-2x;
x2+x-6=0;
(x+3)(x-2)=0;
x=2; x=-3.
Перший корінь не належить ОДЗ, отже єдиний розв'язок рівняння з коренями x=-3.
Відповідь: -3.
Залишайтеся з нами і підготовка до ЗНО з математики залишиться для Вас приємним спогадом та зекономить багато часу та грошей на репетиторів.
Відповіді до ЗНО тестів
- ЗНО 2017 відповіді з математики
- Попередня стаття - ЗНО 2017 математики. Логарифмічні рівняння і нерівності
- Наступна стаття - ЗНО 2017 математика. Ірраціональні рівняння


