Шановні школярі, випускники, абітурієнти, цей розділ допоможе підготуватися до зовнішнього оцінювання 2017 року. Відповіді до тестів допоможуть Вам зрозуміти матеріал та методику обчислень , систематизувати та підвищити накопичений рівень знань з математики.
Розділ II. Рівняння і нерівності
Завдання 2.29 Розв'яжіть логарифмічну нерівність
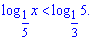
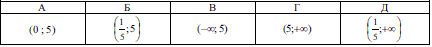
Розв'язання: Основа логарифма менша одиниці тому для розкриття слід поміняти знак нерівності. Але ми цього робити не будемо, а покажемо як вивести це правило самостійно. Нерівність можна перетворити згідно властивостей логарифма
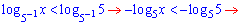
переносимо обидві частини за знак нерівності
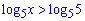
та розкриваємо нерівність x>5, отже маємо такий розв'язок нерівності
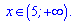
Інтервал наведений в тестах під варіантом Г.
Відповідь: Г.
Завдання 2.30 (Т-06, 17) Розв'яжіть нерівність
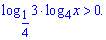
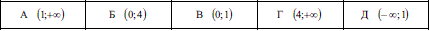
Розв'язання: Спершу слід завжди виписувати умову на область допустимих значень (ОДЗ) логарифма x>0.
Далі потрібно оцінити кожен з доданків, перший приймає значення
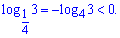
Отже, щоб виконувалась умова другий множник теж має приймати від'ємне значення
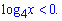
Далі розкриваємо нерівність за правилом
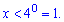
Разом з умовою на ОДЗ це дасть інтервал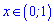 
, який у відповідях до тестів йде під варіантом В.
Відповідь: В.
Завдання 2.31 (Т-07, 16) Розв'яжіть нерівність
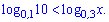
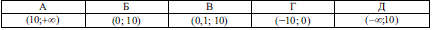
Розв'язання: За властивостями логарифма, якщо основи менші за одиницю то при розкритті нерівності міняємо знак на протилежний.
Але можна піти іншим шляхом і перетворити основи так, щоб вони були більші за одиницю. Перетворимо для цього логарифми
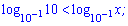
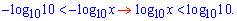
При розкритті нерівності отримаємо x<10.
Крім цього ОДЗ логарифма дає обмеження на інтервал з лівої сторони осі x>0.
Розв'язком нерівності є інтервал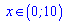 
. Він відповідає варіанту Б ЗНО тестів.
Відповідь: Б.
Залишайтеся з нами і підготовка до ЗНО з математики залишиться для Вас приємним спогадом та зекономить багато часу та грошей на репетиторів.
Відповіді до ЗНО тестів
- ЗНО 2017 відповіді з математики
- Попередня стаття - ЗНО 2017 математика. Показникові рівняння і нерівності
- Наступна стаття - ЗНО 2017 математика. Змішані рівняння
