ЗНО математика. Задачі з ймовірності

Шановні школярі, випускники, абітурієнти, цей розділ допоможе підготуватися до зовнішнього незалежного оцінювання з математики 2017 року. Відповіді до тестів допоможуть засвоїти теоретичний матеріал та методику обчислень, систематизувати та підвищити накопичений рівень знань з математики.

Розділ IV. Елементи комбінаторики, початки теорії ймовірностей та елементи статистики

Завдання 4.1 - 4.9 мають по п'ять варіантів відповідей, із яких тільки одна правильна. Правильно виконане завдання оцінюється 1 балом.

Задача 4.8 Скількома різними способами можна скласти трикольоровий прапор з горизонтальними смугами заданої ширини (див. рис.), якщо є тканина шести різних кольорів?
ЗНО тести Розв'язання: Розпишемо всі можливі комбінації кольорів прапора.
Перший колір можна вибрати 6 способами, другий – на одиницю менше 5 (оскільки один колір вже вибрали) і третій – 4 способами. Кількість способів обчислюємо множенням варіантів вибору усіх трьох смуг прапора
6*5*4=30*4=120.
За такою схемою обчислюють подібні задачі комбінаторики.
Відповідь: В.

Задача 4.9 У квадраті зі стороною 4 см відмічають точку. Яка імовірність того, що відстань від цієї точки до найближчої сторони квадрата менше 1 см?
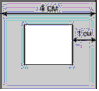
ЗНО тести Розв'язання: Маємо геометричну задачу на ймовірність. Все що потрібно для обчислення ймовірності – це площу заштрихованої частини квадрата розділити на площу всього квадрата. Обчислимо площі
S= 4^2=16;
2*2=4;
S₁=16-4=8.
Далі знаходимо ймовірність діленням відповідних площ
P=8/16=1/2.
Результат відповідає варіанту Г ЗНО тестів.
Відповідь: Г.

В Задачах 4.10 - 4.11 правильна відповідь оцінюється 2 балами.

Задача 4.10 Учаснику телевізійного шоу дозволяється відімкнути довільні два сейфи із п'яти запропонованих (у двох із них лежать призи, а інші - порожні). Обчисліть ймовірність отримання двох призів.
Розв'язання: Ймовірність відкрити першим сейф з призом рівна 2/5, оскільки маємо в 2 призи, а всього 5 сейфів. Після цього, чисто теоретично, залишається 4 сейфи і 1 приз, тобто ймовірність вгадати 2 сейф рівна 1/4. Сумарна ймовірність взяти обидва призи за теоремою про сумування ймовірностей рівна їх добутку

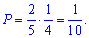
Значення 0,1 дає надію, що кожен 10 учасник телевізійного шоу може «зірвати банк».
Відповідь: 0,1.

Задача 4.11 Середній вік одинадцяти футболістів команди становить 22 роки. Під час гри одного з футболістів було вилучено з поля, після чого середній вік гравців, що залишилися, став 21 рік. Скільки років футболісту, який залишив поле? (Т-07, 26)
Розв'язання: Багатьом може здатися, що завдання складне, але це не так. Давайте міркувати так: в футбольній команді одинадцять граків.
Помножимо середній вік на кількість футболістів і ми будемо знати сумарно роки гравців всієї команди
11*22=242.
Після вилучення одного гравця їх кількість дорівнює 10.
За наведеною ж схемою визначаємо вік 10 гравців, враховуючи, що їх середній вік 21 рік.
10*21=210.
Різниця між знайденими значеннями і є віком гравця, що залишив поле
242-210=32 (роки).
Після обчислень задача багатьом здається зовсім не важкою, хоча на тестах її віднесли до складних.
Відповідь: 32.