ЗНО математика. Похідна функції в точці

Шановні школярі, випускники, абітурієнти, цей розділ допоможе підготуватися до зовнішнього незалежного оцінювання з математики у 2017 року. Відповіді до тестів допоможуть Вам зрозуміти матеріал та методику обчислень, систематизувати та підвищити накопичений рівень знань з математики.

Розділ III. Функції

Завдання 3.1 - 3.45 мають по п'ять варіантів відповідей, із яких тільки одна правильна. Правильно виконане завдання оцінюється 1 балом.

Завдання 3.29 На рисунку зображено графік функції у=f(х). Знайдіть найбільше значення функції
z=log_0,5f(x).

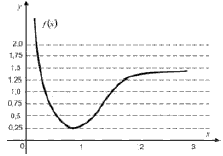
Розв'язання: З вигляду логарифма бачимо, що чим менше значення приймає функція, ти більше приймає логарифм. Мінімум функції рівний 0,25. Обчислюємо логарифм

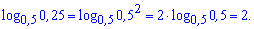
Отримали значення 2, яке відповідає варіанту А тестів.

Завдання 3.30 Знайдіть похідну функції f(х)=6*х²+е^4х-4 у точці x₀=1.

Розв'язання: Обчислюємо похідну функції за табличними формулами
f'( х ) = 12 *х + 4*е^4х-4 .
Далі знаходимо значення похідної в точці
f'( х ) = 12 *1 + 4*е^4*1х-4=12+4*e⁰=12+1=13.
Із наведених варіантів відповідей Г містить правильну відповідь.

Завдання 3.31 Обчисліть f'(-1), якщо f (х)=2/(1-x).

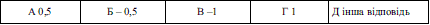
Розв'язання: За правилами диференціювання отримаємо логарифм. Знак буде від'ємний, оскільки ще доведеться брати похідну від дужки
похідна функції
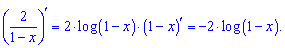
Підставимо точку у похідну
f'( -1)=-2*log(2).
Варіанти А-Г не містять потрібного значення, отже залишається інша відповідь – Д.
Відповідь: Д.