Нижче наведена таблиця містить основні формули похідних. З їх допомогою можна знайти більшість похідних і таблицю потрібно, якщо не знати на зубок, то хоча б мати під рукою для використання при вивченні диференціювання (знаходженні похідних).
Запишемо правила знаходження похідних
1) 
2) 
3) 
4) 
5) 
6) 
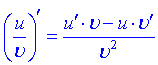
Тут С – стала величина (константа), 
– функції від аргументу x, що мають похідні.
7) Якщо маємо
– складену функція, тобто y=f(u), а u в свою чергу фунція від аргументу
, та існують окремо похідні обидвох функцій 
і 
, то існує похідна від y по x, причому
Використовуючи наведене правило похідної складеної функції, таблицю похідних запишемо так
8) 
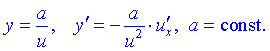
9) 
10) 
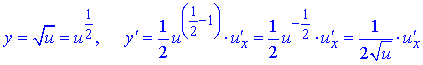
11) 
12) 
13) 
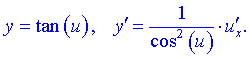
14) 
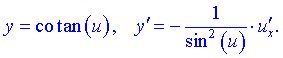
15) 
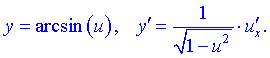
16) 
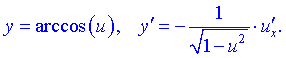
17) 
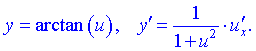
18) 
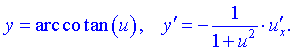
19) 
20) 
21) 
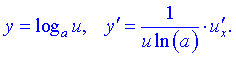
22) 
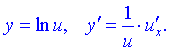
23) 
В наступних статтях будуть показані правила диференціювання, враховуючи наведену таблицю похідних.
Якщо наведених формул похідних Вам мало (потрібні еліптичні чи інші спеціальні функції), то можете знайти онлайн в інтернеті та завантажити довідник з "формулами диференціювання" та теоремами, які застосовують при знаходженні похідних.
