Шановні школярі, випускники, абітурієнти, цей розділ допоможе підготуватися до зовнішнього незалежного оцінювання з математики у 2017 року.
Відповіді до тестів допоможуть Вам зрозуміти матеріал та методику обчислень, систематизувати та підвищити накопичений рівень знань з математики.
Розділ III. Функції
Розв'язання завдань 3.63 - 3.68 повинне мати обґрунтування. Запишіть послідовні логічні дії та пояснення, зробіть посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв'язання завдань схемами, графіками, таблицями.
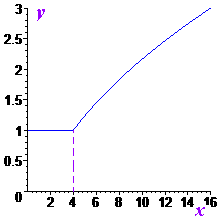
Завдання 3.63 Побудуйте графік функції
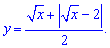
Розв'язання: Задана ірраціональна функція, вигляд якої не надто складний. Умова на область визначення для коренів x>0 показує на якій області слід аналізувати та будувати функцію. Крім того маємо в чисельнику модуль, який розбиває інтервал на дві частини Знайдемо точку перелому графіка
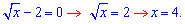
Далі записуємо кінцеве рівняння для побудови графіка функції до і після цієї точки. Розкриваючи модуль, отримаємо
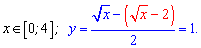
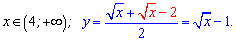
Першу функцію може побудувати кожен школяр. Друга – коренева функція опущена на 1 вниз по осі Oy.
Кореневу для зручності будуємо по точках в яких легко взяти корінь – 9, 16, 25.
Графік функції має вигляд
Приблизно таким має бути аналіз для побудови графіка функції.
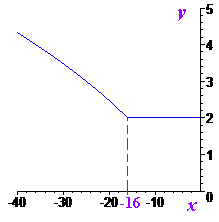
Завдання 3.64 (Т-07, 12) Побудуйте графік функції
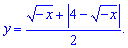
Розв'язання: Починаємо аналіз з ОДЗ. Підкоренева функція повинна бути додатною, це дає нам умову
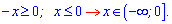
Далі визначаємо нуль модуля
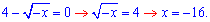
Розкриваємо модуль і записуємо рівняння функції до і після цієї точки
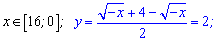
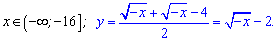
Як будувати корінь Ви повинні знати. На першому проміжку функція стала, тобто будуємо пряму.
Графік функції матиме вигляд
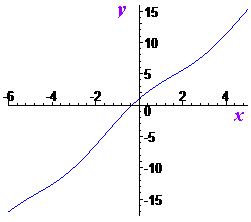
Завдання 3.65 Задано функцію f(x)=3x+cos( x).
1. Визначте проміжки зростання та спадання функції f(x.)
2. Розв'яжіть рівняння
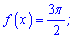
Розв'язання: 1. Функція визначена на всій дійсній осі. Перевіримо чи має функція точки екстремуму. Для цього обчислюємо похідну і прирівнюємо її до нуля

Враховуючи область значень синуса, похідна f '>0 всюди додатна. Отже функція зростає на всій множині значень.
Графік функції хвилеподібний
2. Розв'яжемо тригонометричне рівняння
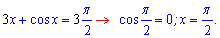
Розв'язком є кут 90 градусів.
Залишайтеся з нами і підготовка до ЗНО з математики залишиться для Вас приємним спогадом та зекономить багато часу та грошей на репетиторів.
Відповіді до ЗНО тестів
- Розв'язки ЗНО відповіді з математики
- Попередня стаття - ЗНО 2017 математика. Інтегрування функцій
- Наступна стаття - ЗНО 2017 математика. Аналіз функції