ЗНО математика. Об'єм паралелепіпеда, піраміди

Шановні школярі, випускники, абітурієнти, цей розділ допоможе підготуватися до зовнішнього оцінювання 2017 року. Відповіді до тестів допоможуть Вам зрозуміти матеріал та методику обчислень при підготовці, систематизувати та підвищити накопичений рівень знань з математики. Рішення прикладів з математики будуть цікаві для школярів 9, 10, 11 класів, а також їх батьків.

Розділ 6. Стереометрія

В завданнях 6.22 - 6.37 правильна відповідь оцінюється 2 балами.
Задача 6.25 Прямокутний паралелепіпед з довжиною ребер 5 см, 7 см і 9 см складено з кубиків з довжиною ребра 1 см.
Скільки доведеться забрати кубиків, щоб вилучити весь зовнішній шар товщиною в один кубик?
Розв'язання: Завдання одночасно і доволі просте і складне, якщо піти неправильним шляхом. Додаткової побудови виконувати не потрібно, завдання і без цього зрозуміле.
Можна обчислити покроково поверхні паралелепіпеда, але це довгий і неправильний шлях. Простіше знайти об'єм заданого паралелепіпеда і внутрішнього.
Для обчислення внутрішнього потрібно знайти його сторони, які рівні заданим мінус 2 сантиметри (здогадайтесь чому).
В результаті знаходимо об'єми
V=5*7*9=315 (сантиметрів кубічних);
V1=3*5*7=105 (сантиметрів кубічних).
Різниця об'ємів точно рівна кількості кубиків з ребром в 1 см
315-105=200.
Добре проаналізуйте для себе дану задачу.
Схема обчислень дозволяє зекономити багато часу на тестах і зрозуміла для пояснення школярам.
Відповідь: 200.
Задача 6.26 Обчисліть об'єм многогранника (у см ), усі вершини якого лежать у центрах граней прямокутного паралелепіпеда з вимірами 3 см, 4 см, 5 см.
Розв'язання: Важко спершу уявити, що потрібно обчислювати, проте побудова багато на що відкриває очі.

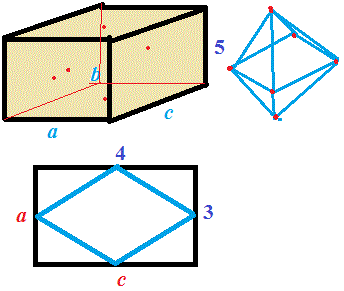
Об'єм потрібної фігури рівний об'єму двох пірамід в основі яких ромб, причому діагоналі ромба рівні сторонам грані паралелепіпеда - 3 і 4 см.
Висота кожної з пірамід рівна половині висоти сторони 5/2=2,5 см.
Площа ромба рівна половині площі прямокутника (випливає з побудови)
S=3*4/2=6 (сантиметрів квадратних).
Далі знаходимо об'єм потрібної фігури
V=1/3*6*2,5*2=10 (сантиметрів кубічних).
Простіших міркувань для обчислення задачі з планіметрії і бути не може. Великим плюсом в обчисленнях є виконання побудови до умови задачі.
Це дозволяє спростити знаходження площ, об'ємів до кількох простих і зрозумілих усім дій.
Привчайте себе виконувати побудову в прикладах з геометрії, планіметрії.
Відповідь: 10.
Задача 6.27 Об'єм правильної чотирикутної піраміди SАВСD дорівнює 60 м . Точка К - середина ребра SС. Обчисліть об'єм піраміди КВСD, у см3

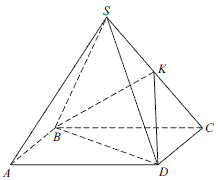
Розв'язання: Розв'язок можна знайти з пропорцій піраміди- це найлегший шлях.
Запам'ятайте: Формула об'єму циліндрів, паралелепіпедів, пірамід – це завжди добуток площі основи на висоту і на певний коефіцієнт, який визначає фігуру.
В нашому випадку в основі піраміди квадрат, діагональ якого розбиває основу на рівні за площею трикутники. Висота трикутної піраміди рівна половині висоти правильної чотирикутної - це випливає з пропорцій.
Звідси об'єм трикутної піраміди рівний четвертій частині об'єму повної
V1=V/(2*2)=60/4=15 (сантиметрів кубічних).
Таким чином знайти об'єм піраміди без складних формул можна завжди, головне знати властивості фігур. В подібних завданнях старайтесь використовувати пропорції, прості закономірності, які дозволяють в швидкий час виписати нові формули, зробити правильні висновки та в легкий спосіб отримати правильний результат.
Відповідь: 15.
Допомога з математики у вигляді готових рішень полегшить навчання всіх школярів і буде гарною інструкцією на іспитах і тестах. Готові тестові приклади обов'язково стануть в нагоді у навчанні школярам в 9, 10, 11 класі. Залишайтеся з нами і підготовка до ЗНО з математики залишиться для Вас приємним спогадом та зекономить багато часу та грошей на репетиторів.