ЗНО математика. Площа поверхні, об'єм піраміди

Шановні школярі, випускники, абітурієнти, цей розділ допоможе при підготуватися до зовнішнього оцінювання 2017 року. Відповіді до тестів допоможуть Вам зрозуміти матеріал та методику обчислень при підготовці, систематизувати та підвищити накопичений рівень знань з математики. Рішення прикладів з математики будуть цікаві для школярів 9, 10, 11 класів, а так само їх батьків.

Розділ 6. Стереометрія

В завданнях 6.22 - 6.37 правильна відповідь оцінюється 2 балами.
Задача 6.28 В основі піраміди лежить трикутник зі сторонами 5, 6 та 8 см, а всі бічні ребра піраміди нахилені до площини основи під кутом 45°. Обчисліть об'єм піраміди, у см ³.
Розв'язання: Завдання для шкільного рівня знань надто складне. Тут потрібно використати властивість, згідно якої маємо : якщо ребра піраміди нахилені під однаковим кутом до основи, то вершина піраміди рівновіддалена від вершин. Крім цього проекція висоти на основу співпадає з центром описаного кола навколо трикутника основи.

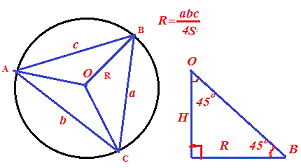перерізи піраміди Далі оскільки ребра мають кут нахилу 45 градусів, то висота піраміди рівна радіусу описаного кола. Таким чином, для обчислення об'єму необхідно знайти радіус описаного кола (висоту) і площу трикутника зі сторонами 5,6 і 8.
Площу основи коли відомі сторони знайти можна за формулою Герона. Радіус описаного кола знаходимо за формулою
R = a*b*c /( 4*S).
З формули бачимо, що обчислення об'єму спрощується
V = H*S =1/3* a*b*c /( 4*S)*S= a*b*c /12.
Ми тільки що вивели формулу об'єму трикутної піраміди, ребра якої нахилені під кутом 45 градусів до основи.
Виконуємо обчислення
V=4*5*6/12=20.
Відповідь: V = 20.

Задача 6.29 (Т-06, 12) Висота правильної чотирикутної піраміди дорівнює 3 см. Апофема утворює з площиною основи кут 60°. Обчисліть площу бічної поверхні піраміди (у см ).
Розв'язання: Правильна чотирикутна піраміда в основі має квадрат. Апофема – це висота ребра піраміди. Кут при вершині піраміди між її висотою і висотою на ребрі рівний
90-60=30 градусів.
Звідси слідує, що висота ребра вдвічі більша за катет трикутника, який в свою чергу рівний половині сторони квадрата. Таким чином висота ребра і сторона квадрата між собою рівні. Залишилося знайти гіпотенузу прямокутного трикутника і пощу бічної поверхні, як площу 4 рівнобедрених трикутників можна буде знайти. За означення синус кута рівний відношенню протилежного до кута катета до гіпотенузи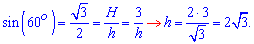
Далі знаходимо площу бічної поверхні піраміди
площа поверхні піраміди
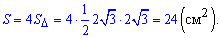
Відповідь: 24.

Задача 6.30 (Т-07, 23) Для опалювальної системи будинку необхідні радіатори із розрахунку: три одиниці на 50м . Яку кількість одиниць радіаторів треба замовити, якщо новий будинок має форму прямокутного паралелепіпеда розміру 15м*18м*25м?
Розв'язання: Спершу знаходимо об'єм будинку
V=15*18*25=6750 (метрів кубічних).
Далі ділимо об'єм будинку на 50
6750/50=135.
Знайдену кількість множимо на 3, оскільки потрібно 3 радіатори на 50 метрів кубічних.
135*3=405.
На тестуванні багато з учасників останню дію в обчисленнях пропустили, тому будьте уважні і добре читайте умову завдань.
Відповідь: 405.

Задача 6.31 (Т-07, 23) Апофема правильної чотирикутної піраміди дорівнює 2 Pi/3 см і нахилена під кутом 60° до площини основи. Знайдіть об'єм піраміди.
Розв'язання: Відомо, що висота ребра з основою складають кут 60 градусів. Відповідно кут при вершині рівний 30. Звідси слідує, що апофема і сторона онови піраміди рівні між собою і
а=2 Pi/3.
Висоту знаходимо через синус

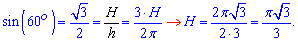
Обчислюємо об'єм піраміди за формулою

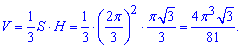
Це і є відповіддю до тестового завдання.
Допомога з математики у вигляді готових рішень полегшить навчання всіх школярів і буде гарною інструкцією на іспитах і тестах. Готові тестові приклади обов'язково стануть в нагоді у навчанні школярам в 9, 10, 11 класі. Залишайтеся з нами і підготовка до ЗНО з математики залишиться для Вас приємним спогадом та зекономить багато часу та грошей на репетиторів.