Наведені розв'язки ЗНО з математики за 2013 р. допоможуть, а декого і навчать, розв'язувати подібні завдання при проходженні зовнішнього незалежного оцінювання в 2014 та наступних роках. Завдання викладені послідовно і зрозуміло, тож лишається уважно розібратися з відповідями.
Завдання 22. У прямокутній системі координат на площині xy задано точки О(0;0) і А(6;8). З точки А на вісь х опущено перпендикуляр. Точка В – основа цього перпендикуляра. Установіть відповідність між величиною (1-4) та її числовим значенням (А-Д)
Величина
1. ордината точки В
2. довжина вектора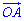 
3. довжина радіуса кола, описаного навколо трикутника ОАВ
4. відстань від точки А до осі х
Варіанти відповідей:
А) 0
Б) 5
В) 6
Г) 8
Д) 10
Розв'язання: Побудуємо допоміжний графік.
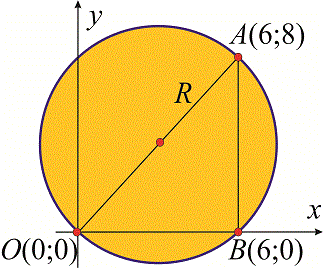
З малюнку бачимо, що ордината точки В рівна нулю. Тобто на перше завдання відповідь 1–А).
Знаючи координати початку координат і точки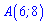 
довжину вектора 
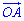знаходимо за формулою
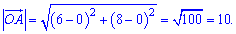
Тобто варіант Д). Так як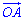 
є діаметром описаного кола, то його радіус рівний половині, тобто 5 (відповідь 3–Б).
Відстань від точки А до осі х рівно ординаті точки 8 (відповідь 4–Г).
Виконуйте додаткову побудову там, де це необхідно, оскільки часто правильне графічне представлення умови задачі містить в собі частину розв'язку завдання.
Відповідь: 1-А), 2-Д), 3-Б), 4-Г).
------------------------------
Завдання 23. Дві однакові автоматичні лінії виготовляють 16 т шоколадної глазурі за 4 дні. Установіть відповідність між запитаннями (1-4) та правильною відповіддю на нього (А-Д). Уважайте, що кожна лінія виготовляє однакову кількість глазурі щодня.
Запитиння
1. За скільки днів одна лінія виготовляє 16 т шоколадної глазурі?
2. Скільки тонн шоколадної глазурі виготовить одна лінія за 2 дні?
3. Скільки таких ліній потрібно для виготовлення 48 т шоколадної глазурі за 4 дні?
4. Скільки тонн шоколадної глазурі дві ліній виготовляють за 3 дні?
Варіанти відповідей:
А) 2
Б) 4
В) 6
Г) 8
Д) 12
Розв'язання: Вияснимо скільки глазурі виробляє одна лінія за один день. Оскільки обидві лінії виготовляють порівну, то потрібно денну норму розділити на 2
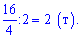
В результаті відшукання правильних відповідей зводиться до простих дій
1. 16 тон за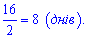 
2. одна лінія за два дні виготовить
2*2=4 (т.)
3. питання не надто складне і вирішується одним рядком
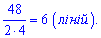
4. питання вирішуємо множенням
2*2*3=12 (т).
Відповідь: 1-Г), 2-Б), 3-В), 4-Д).
------------------------------
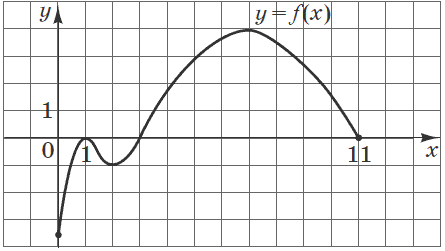
Завдання 24. На рисунку зображено графік функції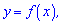 
визначеної на проміжку [0;11] та диференційованої на проміжку (0;11). Установіть відповідність між числом (1-4) та проміжком (А-Д), якому належить це число.
Число
1. найменше значення функції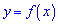
на її області визначення
2. 
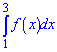
3. 
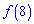
4. 
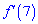
Проміжок
Варіанти відповідей:
А) (
-2]
Б) (
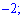-05]
В) (-05;2]
Г) (2;4]
Д) (4; 
]
Розв'язання: Для розв'язання цього завдання необхідно спочатку знайти обмежені розв'язки кожного пункту, а потім вибрати для кожного область, яка найбільш конкретно окреслюватиме розв'язок.
1. Найменше значення функції на проміжку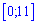 
рівне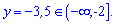 
2. Інтеграл знаходимо з графіку, він лежатиме в межах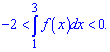 
3. Значення функції при ординаті 8 таке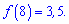 
4. Оскільки дотична до графіку функції в точці х=7 паралельна до осі Ох, то похідну, за означенням, знаходимо через тангенс На основі знайдених значень для кожного варіанту підбираємо правильний інтервал
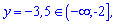
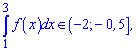
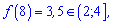
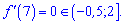
Відповідь: 1-А), 2-Б), 3-Г), 4-В).
------------------------------
Завдання 25. Додатне число А більше додатного числа В у 3,9 раза. На скільки відсотків число А більше за число В?
Розв'язання: Більше у 3.9 раз означає, що рівне 390 % від числа В. Дальше, знаходимо відношення різниці чисел до числа В у процентах
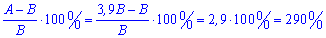
Відповідь: 290.
------------------------------
Завдання 26. Обчисліть значення виразу
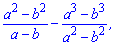
якщо а= -10,2; b= 0,2.
Розв'язання: Дане завдання багато абітурієнтів не розв'язали, оскільки не згадали потрібних формул скороченого множення. Отож зводимо до спільного знаменника та спрощуємо, просумувавши попередньо подібні доданки
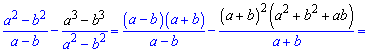
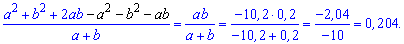
Проблема у декого виникла при множенні, оскільки на ЗНО користуватися калькуляторами заборонено. На нашу думку це неправильно і використання простого калькулятору (без інженерних функцій) дещо зменшить напруженість абітурієнтів при тестуванні. Також не бачимо великої мудрості у перевірці школярів на швидкість виконання операцій множення та ділення у стовпчик.
Відповідь: 0,204.
------------------------------
Завдання 27. Розв'яжіть нерівність
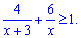
У відповіді запишіть суму всіх цілих її розв'язків.
Розв'язання: Нерівності для багатьох абітурієнтів викликає проблеми, проте до їх розв'язування завжди необхідно підходити з холодною головою. Переносимо одиницю вправо та зводимо до спільного знаменника
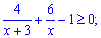
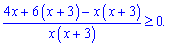
Розкриємо дужки в чисельнику і згрупуємо подібні доданки
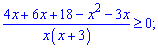
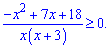
Прирівняємо квадратне рівняння до нуля і знайдемо його корені
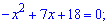
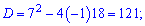
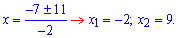
За формулою розкладу рівняння записуємо у вигляді
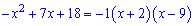
та переписуємо нерівність
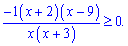
Нулі чисельника та знаменника позначаємо на числовій осі та розв'язуємо нерівність методом інтервалів. Для зручності домножуємо праву і ліву частину нерівності на мінус одиницю і міняємо знак на протилежний.
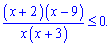
Отриману нерівність розв'язуємо методом інтервалів.
В подібних прикладах не забувайте виключити з розв'язку нулі знаменника, вони не можуть бути розв'язком.
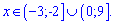
Дальше виконуємо сумування цілих розв'язків
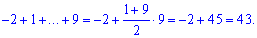
Тут для спрощення використано арифметичну прогресію.
Відповідь: 43.
------------------------------
Переглянути розв'язки завдань № 16-21 ЗНО-2013 математика та розв'язки завдань № 28-33 ЗНО-2013 математика
