Пройти пробний онлайн тест з математики Ви можете на ряді інтернет ресурсів, це вимагає від Вас уваги та часу. Нижче пропонуємо ознайомитися з готовими розв'язками тестів із ЗНО математика за 2013 рік. Подібні завдання будуть зустрічатися і при оцінюванні в 2014, 2015 та наступних роках.
Завдання 16. Спростити вираз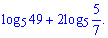 
Варіанти відповідей:
А) 25;
Б)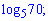 
В)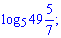 
Г) 
Д) 2.
Розв'язання: Для спрощення виразу застосуємо властивості логарифма. Перепишемо перший доданок
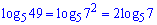
та просумуємо
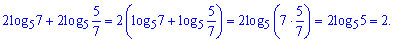
При обчисленні подібних виразів потрібно добре знати властивості логарифмів. Незнання потрібного правила може привести до зупинки в обчисленнях, навіть якщо до результату залишається лише одна дія. Випишіть усі перетворення з логарифмами та старайтеся повторяти їх час від часу на практиці.
Відповідь: Д).
------------------------------
Завдання 17. Менша сторона прямокутника дорівнює 16 м і утворює з його діагоналлю кут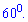 
. Середини всіх сторін прямокутника послідовно сполучено. Знайдіть площу утвореного чотирикутника.
Варіанти відповідей:
А)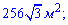 
Б)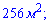 
В)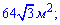 
Г)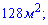 
Д)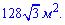 
Розв'язання: Позначимо сторони прямокутника та відомий
кут через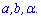 
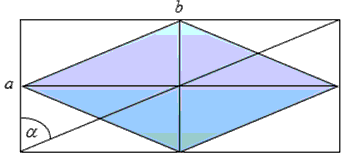
Із прямокутного трикутника, утвореного діагоналлю і сторонами прямокутника, обчислимо значення більшої сторони за формулою
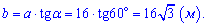
З'єднаємо середини сторін прямокутника, в результаті отримаємо ромб. Крім цього діагоналі ромба за довжиною рівні сторонам прямокутника і є паралельними до них. За властивостями ромба його площа рівна
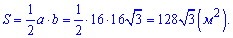
Площу ромба, яка рівна половині площі прямокутника, можна без особливих зусиль знайти візуально з малюнку (якщо не знаєте правила).
Відповідь: Д).
------------------------------
Завдання 18. Укажіть нерівність, що виконується для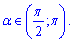 
Варіанти відповідей:
А)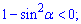 
Б)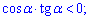 
В)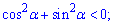 
Г) 
Д)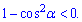 
Розв'язання: Визначимо значення функцій в нерівностях на заданому проміжку. Варіант А) приймає додатнє значення
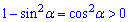
на заданому інтервалі 
, що суперечить завданню. Нерівність Б) можна спростити та записати у вигляді
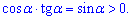
Вона також приймає протилежне значення ніж у завданні на інтервалі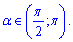
Нерівність В) є важливою теоремою в тригонометрії і перетворюється на тотожність, яка, без сумніву, відома теоретично усім абітурієнтам
Варіант Г) після спрощення матиме наступний вигляд
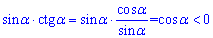
і задовільняє умову завдання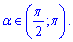 
Остання нерівність приймає протилежне значення
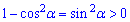
ніж зазначене у варіантах відповідей.
Відповідь: Г).
------------------------------
Завдання 19. У трикутнику АВС вписано квадрат KLMN (див. рисунок). Висота цього трикутника, проведена до сторони АС, дорівнює 6 см. Знайдіть периметер квадрата, якщо АС =10 см.
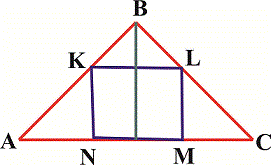
Варіанти відповідей:
А) 15 см
Б) 7,5 см
В) 12,5 см
Г) 17,5 см
Д) 20 см
Розв'язання: Позначимо через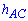 
- висоту трикутника ВСА, проведену до сторони АС, 
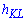– відповідно висота трикутника ВLK до сторони KL. За властивістю пропорцій маємо
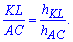
Враховуючи, що сторони квадрата рівні, запишемо висоту трикутника ВLK у вигляді
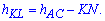
Виконаємо нескладні маніпуляції з пропорціями
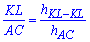
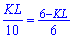
щоб отримати рівняння для визначення сторони квадрату
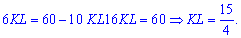
Периметр квадрату знаходимо за відомою формулою
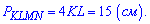
Відповідь: А).
------------------------------
Завдання 20. Переріз кулі площиною має площу 81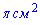
. Знайдіть відстань від центра кулі до площини перерізу, якщо радіус кулі дорівнює 15 см.
Варіанти відповідей:
А) 12 см
Б) 8 см
В) 6 см
Г) 9 см
Д) 15 см
Розв'язання: Дане завдання розв'яжемо на основі наступних міркувань. Переріз куруга площиною завжди дає в перерізі круг. Знаючи формулу площі круга
,
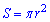з початкової умови
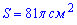
знаходимо його радіус
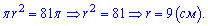
Намалюємо переріз так, щоб він зливався в пряму.
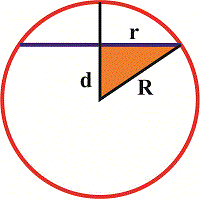
З прямокутного трикутника знаходимо потрібну відстань
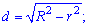
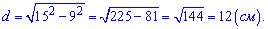
Відповідь: А).
------------------------------
Завдання 21. Установіть відповідність між фігурою (1-4) і тілом обертання (А-Д), яке утворено внаслідок обертання цієї фігури навколо прямої, зображеної пунктиром.
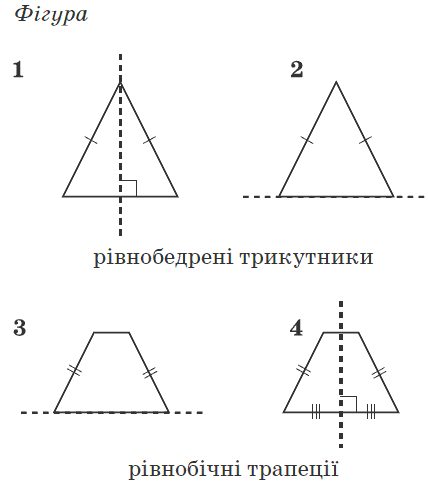
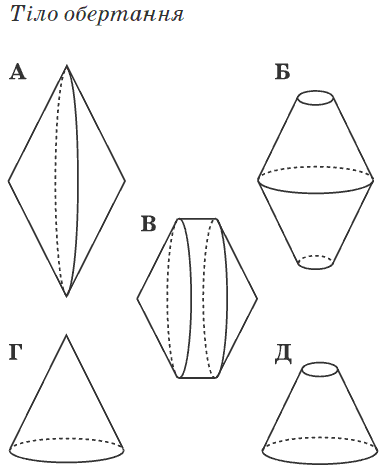
Розв'язання: Завдання не надто складне, однак найкраще його вдається виконати школярам з добре розвинутою просторовою уявою. Для отримання тіла обертання можна виконати малюнки, в яких з віддалених від осі точок побудувати еліпси, більші осі яких рівні відстані до осі обертання. Також ці точки симетрично відобразити відносно осі і з'єднати лініями. В результаті отримаємо об'ємний вигляд фігур обертання.
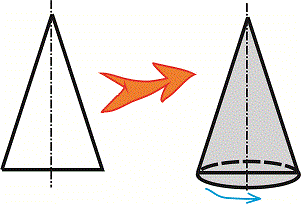
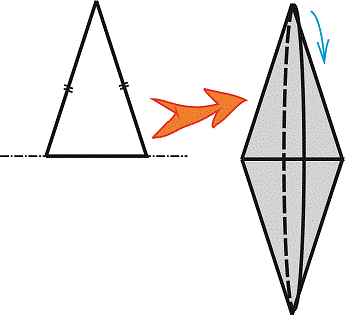
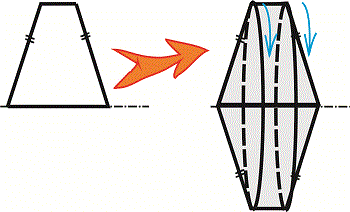
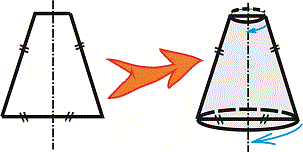
Повернемо деякі графіки на 90 градусів і прирівняємо до варіантів відповідей.
Відповідь: Без труднощів знаходимо, що фігурі 1 відповідає об'ємний вигляд А), 2 – Г), 3 – Д), 4 – В).
------------------------------
Переглянути розв'язки завдань № 10-15 ЗНО-2013 математика та розв'язки завдань № 22-27 ЗНО-2013 математика
