Відповіді на останні питання ЗНО-2013 з математики найактуальніші і їх найчастіше шукають в інтернеті. Справа в тому, що за ці завдання можна отримати найбільше балів і мало кому з учасників вдалося правильно розв'язати вказані завдання. Дані варіанти взяті із другої сесії тестування.
------------------------------
Завдання 29. У прямокутний трикутник АВС вписане коло, яке дотикається катетів АС та ВС і точках К і М відповідно. Знайдіть радіус кола, описаного навколо трикутника АВС (у см), якщо АК= 4,5см, МВ= 6см.
Розв'язання: Для розв'язку завдання потрібно знати властивості кіл вписаних та описаних навколо трикутника, а самі обчислення достатньо прості. Побудуємо допоміжний графік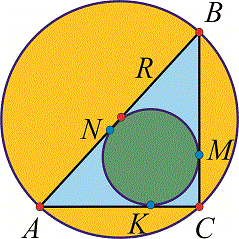
За властивістю відрізків, на які ділить вписане коло в точках дотику з сторонами AB,ВC і AC маємо:
AN=AK, CK=CM, BN=BM.
На основі вище викладеного обчислюємо довжину гіпотенузи трикутника
AB=AN+BN=AK+MB=4,5+6=10,5 (cм).
Оскільки радіус описаного кола рівний половині гіпотенузи, то залишилося розділити знайдене значення на 2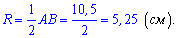 
Відповідь: 5,25 .
------------------------------
Завдання 30. Обчисліть площу фігури, обмеженої графіком функції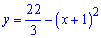 
і прямими 
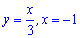та 
.
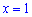Розв'язання: Для відшукання площі фігури потрібно вияснити взаємне розміщення кривих. Нижче наведено рисунок із замальованою областю, площу якої потрібно знайти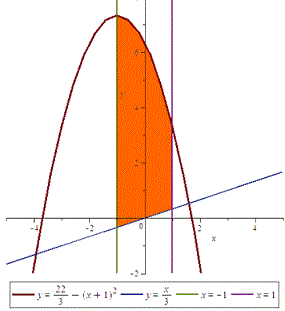 
При тестуванні Ви точно не матимете подібного рисунку, а обчислювати інтеграл потрібно. В цьому випадку потрібно провести наступний аналіз. Інтегрування, як правило, проводять по змінній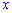 
. За даними прямі 
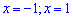будуть межами інтегрування.
Залишилося встановити, яка з кривих
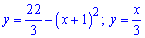знаходиться вище на рисунку, а яка нижче. Якщо цього не зробити, то площа може вийти від'ємною. Для перевірки знаходимо значення в точці 
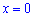, яка належить області інтегрування
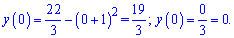
Отже перша крива знаходиться вище. За правилом знаходження площ, від верхньої кривої віднімаємо нижню та інтегруємо в межах [-1;1]
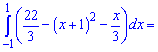
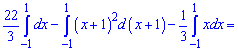
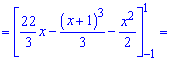
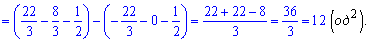
Відповідь: 12 .
------------------------------
Завдання 31. У фестивалі беруть участь 25 гуртів, серед яких є по одному гурту з України і Чехії. Порядок виступу гуртів визначається жеребкуванням, за яким кожен із гуртів має однакові шанси отримати будь - який порядковий номер від 1 до 25. Знайдіть ймовірність того, що на цьому фестивалі гурт з України виступатиме першим, а порядковий номер виступу гурту з Чехії буде парним.
Розв'язання: Нехай подія А – Україна виступає першою, подія В – Чехія виступає під парним номером. Ймоврність визначаємо за класичною формулою
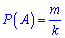
Ймовірність, що Україна виступить першою рівна
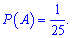
Після виконання події А залишиться 24 команди, кожна друга з яких може виступити під парним номером, тобто
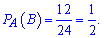
За правилом знаходимо ймовірність через добуток
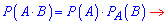
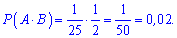
Відповідь: 0,02
------------------------------
Завдання 32. Основою піраміди є ромб, тупий кут якого дорівнює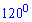 
. Дві бічні грані піраміди, що містять сторони цього кута, перпендикулярні до площини основи, а дві інші бічні грані нахилені до площини основи під кутом 
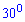. Знайдіть площу бічної поверхні піраміди (у 
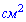), якщо її висота дорівнює 4 см
Розв'язання: Наведемо допоміжний рисунок на основі даних завдання.
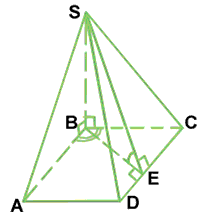
Нехай SABCD – піраміда , ABCD – ромб в її основі.
Два кути основи відомі
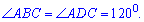
Знаходимо сусідні кути
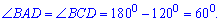
Висота основи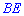 
перпендикулярна до сторони 
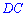. Також з перпендикулярності бічних граней піраміди слідує наступне
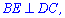
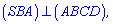
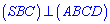
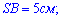
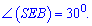
Трикутники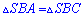 
рівні, оскільки одна сторона 
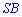спільна, 
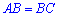і кути при основі прямі
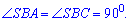
Це означає, що сторони рівн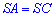і 
і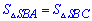 
. За властивістю ромба також отримаємо наступні рівності
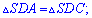
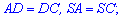
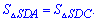
На основі викладеного вище бічна поверхня піраміди обчислюється сумуванням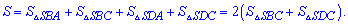 
Площі трикутників можна знайти за формулами
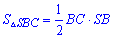і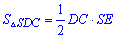 
які після підстановки дають такий вклад
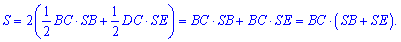
Розглянемо по черзі два трикутники
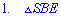
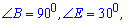
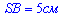– катет навпроти кута
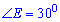рівний половині гіпотенузи 
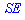, звідси знаходимо гіпотенузу
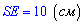
і довжину другого катета
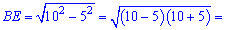
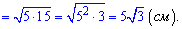
Також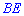 
є висотою рівностороннього трикутника 
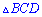, оскільки отримаємо , що всі кути рівні 
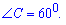А це значить, що 
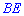можна визначити за формулою
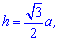де 
– сторона рівностороннього трикутника (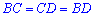
).
Таким чином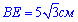 
і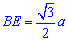 
. Прирівнюємо значення для відшукання сторони
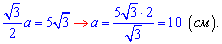
Маємо всі необхідні значення для знаходження площі бічної поверхні піраміди
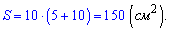
Відповідь: 150.
------------------------------
Завдання 33. При якому найбільшому від'ємному значенні параметра 
рівняння
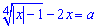
має один корінь?
Розв'язання: Рівняння досить складне, тому підемо простим шляхом. Відомо, що параметр 
від'ємний, відповідно ліва сторона рівняння також від'ємна. Однак вона містить корінь четвертого степеня, який завжди додатній для всіх значень з ОДЗ.
Перепишемо рівняння у вигляді
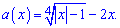
Знайдемо ОДЗ
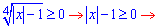
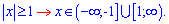
Оскільки параметр 
менший нуля, то значення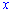 
повинні бути додатніми.
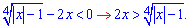
Відповдно для додатніх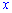 
модуль можна зняти
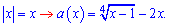
Для знаходження найбільшого значення обчислимо першу похідну функції та прирівняємо її до нуля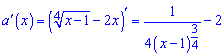 
Визначимо критичні точки, для цього прирівнюємо до нуля і розв'язуємо
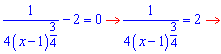
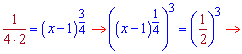
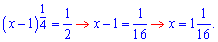
Для перевірки, що знайдена точка є точкою максимуму необхідно переконатися, що вона міняє знак з «+» на «-». Оскільки похідна дала одну точку, а нам потрібна точка максимуму, то не думаю, що завдання придумували так, щоб воно не мало правильної відповіді.
Підставим знайдене значення в формулу і знайдемо найбільше від'ємне значення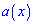 
на проміжку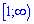 
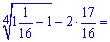
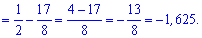
Відповідь: -1,625.
------------------------------
Переглянути відповіді до завдань № 23-28 ЗНО-2013 математика
