Базисом простору називають таку систему векторів, що всі інші вектори простору можна представити у вигляді лінійної комбінації векторів, що входять в базис.
На практиці це все реалізовується досить просто. Базис, як правило, перевіряють на площині або в просторі, а для цього потрібно знайти визначник матриці другого, третього порядку, складений з координат векторів. Нижче схематично записані умови, за яких вектори утворюють базис
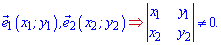
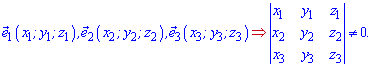
Щоб розкласти вектор b за базисними векторами
e[1],e[2]...,e[n], необхідно знайти коефіцієнти x[1], ..., x[n], при яких лінійна комбінація векторів e[1],e[2]...,e[n] дорівнює вектору b:
x1*e[1]+ ... + x[n]*e[n] = b.
Для цього векторне рівняння слід перетворити до системи лінійних рівнянь і знайти розв'язки. Це також достатньо просто реалізувати.
Знайдені коефіцієнти x[1], ..., x[n], називаються координатами вектора b в базисі e[1],e[2]...,e[n].
Перейдемо до практичної сторони теми.
Завдання 1. Перевірити, чи утворюють вектори a1, a2 базис на площині
1) a1 (3; 5), a2 (4; 2)
Розв'язання: Складаємо визначник з координат векторів
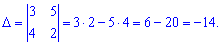
Визначник не дорівнює нулю, отже вектори лінійно незалежні, а значить утворюють базис.
2) a1 (2; -3), a2 (5;-1)
Розв'язання: Обчислюємо детермінант складений з векторів
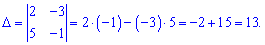
Визначник рівний 13(не рівний нулю), отже вектори a1, a2 є базисом на площині.
Розглянемо типові приклади з програми МАУП з дисципліни "Вища математика".
Завдання 2. Показати, що вектори a1, a2, a3 утворюють базис тривимірного векторного простору, та розкласти вектор b за цим базисом (при розв'язуванні системи лінійних алгебраїчних рівнянь використати метод Крамера).
1) a1 (3; 1; 5), a2 (3; 2; 8), a3 (0; 1; 2), b (−3; 1; 2).
Розв'язання: Спочатку розглянемо систему векторів a1, a2, a3 та перевіримо чи визначник матриці А
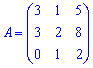
побудованої на векторах відмінний від нуля. Матриця містить один нульовий елемент, тому детермінант доцільніше обчислювати розкладом за першим стовпцем або третім рядком.
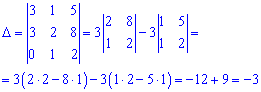
Визначник відмінний від нуля, отже вектори a1, a2, a3 лінійно незалежні. Згідно означення вектори утворюють базис в Е3. Запишемо розклад вектора b за базисом
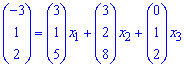
Вектори рівні, коли їх відповідні координати рівні. Тому з векторного рівняння одержимо систему лінійних рівнянь
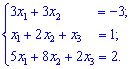
Розв'яжемо СЛАР методом Крамера . Для цього запишемо систему рівнянь у вигляді
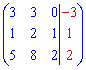
Головний визначник СЛАР завжди рівний визначнику складеному з векторів базису
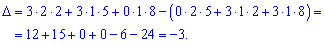
Тому на практиці його не обчислюють двічі. Для знаходження допоміжних визначників ставимо стовпець вільних членів на місце кожного стовпця головного визначника. Визначники обчислюємо за правилом трикутників
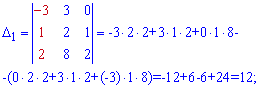
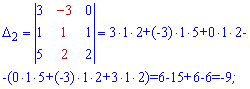
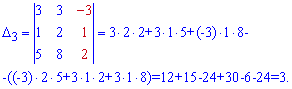
Підставимо знайдені визначники у формулу Крамера
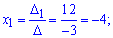
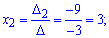
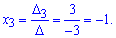
Отже, розклад b за базисом наступний b=-4a1+3a2-a3. Координатами вектора b у базисі a1, a2, a3 будуть (-4,3,-1).
2) a1 (1; -5; 2), a2 (2; 3; 0), a3 (1; -1; 1), b (3; 5; 1).
Розв'язання: Перевіряємо вектори на базис – складаємо визначник з координат векторів та обчислюємо
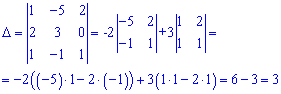
Визначник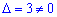 
не дорівнює нулю, отже вектори утворюють базис в просторі. Залишилося знайти розклад вектора b через даний базис. Для цього записуємо векторне рівняння
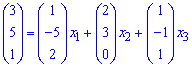
та перетворимо до системи лінійних рівнянь
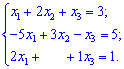
Записуємо матричне рівняння
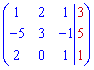
Далі для формул Крамера знаходимо допоміжні визначники
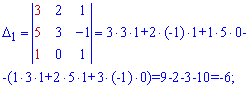
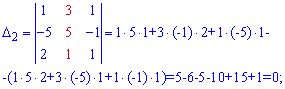
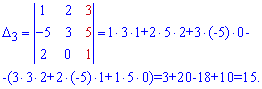
Застосовуємо формули Крамера
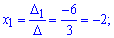
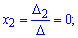
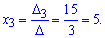
Отже заданий вектора b має розклад через два вектори базису b=-2a1+5a3 а його координати в базисі рівні b(-2,0, 5).
Завдання 3. Довести, що вектори a1, a2, a3 утворюють базис у просторі
1) a1 (3;-2;1), a2 (2; -5; 4) , a3 (2; -3; -1)
Розв'язання: Записуємо координати у визначник та застосовуємо правило трикутників для визначника
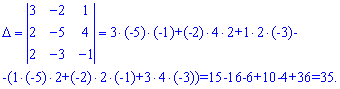
Оскільки визначник (=35) не дорівнює нулю то вектори утворюють базис в просторі.
2) a1 (1; 1;1), a2 (2; -3; 2) , a3 (3; 4; 1)
Розв'язання: Обчислюємо визначник складений з векторів
Det=1*(-3)*1+1*2*3+1*2*4-(1*(-3)*3+1*2*1+1*2*4)=-3+6+8+9-2-8=10 .
Вектори a1, a2, a3 лінійно незалежні (Det=10), а значить утворюють базис в просторі.
Тепер Ви знаєте, як перевірити, що вектори утворюють базис та зможете без проблем розкласти вектор за базисом.
