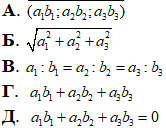Cума векторів за правилом трикутника та паралелограма
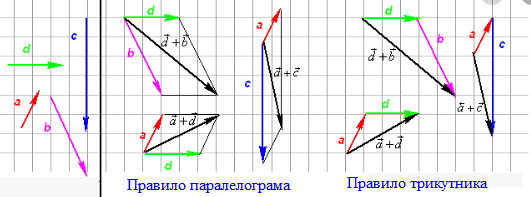
Схема побудови різниці векторів за правилом трикутника та паралелограма
Відповідні формули скалярного добутку векторів, довжини та розрахунку кутів виділені в поясненнях до прикладів червоною рамкою. Для економії часу завантаження сторінки, всюди де йде мова про вектори над ними потрібно писати стрілку  , хоча в тексті ми використовували позначення "вектор а". Це зроблено для покращення індексації сторінки та щоб швидше знайти завдання в пошуку, Ви прирозв'язуванні дотримуйтеся правил (
, хоча в тексті ми використовували позначення "вектор а". Це зроблено для покращення індексації сторінки та щоб швидше знайти завдання в пошуку, Ви прирозв'язуванні дотримуйтеся правил ( ).
).
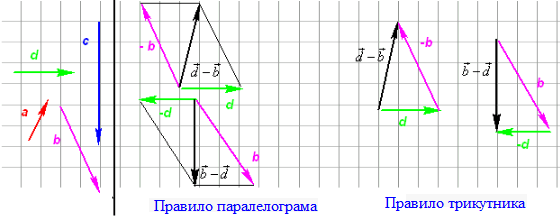
Приклад 42.28 Установити відповідність між векторами (1–4) та їх координатами (А–Д).
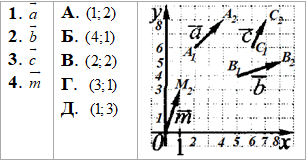
Розв'язування: Знайдемо координати початку та кінця заданих векторів, тоді по них запишемо координати цих векторів:
1. A1(2;6) – початок вектора a,
A2(4;8) – кінець вектора a,
A(4-2;8-6)=(2;2) В.
2. B1(5;4) – початок вектора b,
B2(8;5) – кінець вектора b,
B(8-5;5-4)=(3;1) Г.
3. C1(6;6) – початок вектора c,
C2(7;8) – кінець вектора c,
c(7-6;8-6)=(1;2) А.
4. O(0;0) – початок вектора m,
M2(1;3) – кінець вектора m,
M(1-0;3-0)=(1;3) Д.
Отже, маємо 1 – В, 2 – Г, 3 – А, 4 – Д.
Приклад 42.3 Дано вектори a і b. Який з наведених векторів дорівнює різниці a-b?
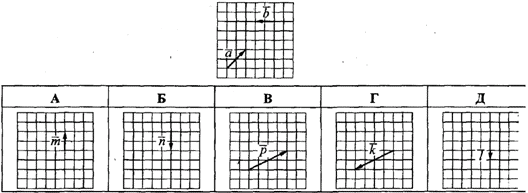
Розв'язування: Відняти вектор a від вектора b означає, що до вектора a треба додати вектор -b (протилежний за напрямком вектору b).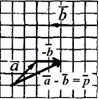
Додавання робитимемо за правилом трикутника:
від кінця вектора a відкладаємо вектор -b, далі суму векторів отримуємо, з'єднавши початок вектора a з кінцем вектора -b, в результаті отримаємо вектор p, тобто
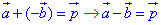
Відповідь: p – В.
Приклад 42.1 Дано паралелограм ABCD. O – точка перетину діагоналей.
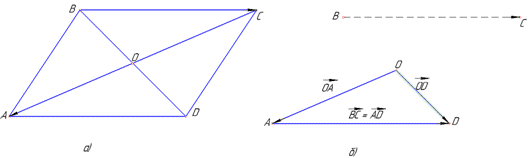
Який з наведених векторів дорівнює сумі BC+OA?
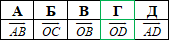
Розв'язування: Паралелограм – чотирикутник, у якого протилежні сторони паралельні та рівні, а діагоналі в точці перетину діляться навпіл. У паралелограма ABCD сторони будемо позначати векторами із заданим напрямком . Звідси слідує, що вектори BC=AD, тобто рівні, бо колінеарні, співнапрямлені та рівні по модулю (довжині). Додавати вектори будемо за правилом трикутника (дивись рисунок б):
від кінця вектора OA відкладаємо вектор AD (він же BC), далі суму векторів отримуємо, з’єднавши початок вектора OA з кінцем вектора BC, в результаті отримаємо вектор OD, тобто OA+BC+OD,
BC+OA=OD.
Відповідь: OD – Г.
Правило трикутника, та як правильно будувати лінійні комбінації векторів Ви повинні поступово вивчити, та пам'ятати, як відкладати вектори,знаходити їх суму та різницю.
Приклад 42.2 Дано вектор a. Який з наведених векторів дорівнює -2/3a?
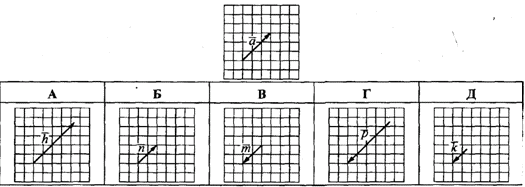
Розв'язування: Перш за все дамо загальні правила масштабування векторів:
Множення вектора  на число λ:
на число λ:
якщо |λ|>1, то вектор  розтягнули у λ разів;
розтягнули у λ разів;
якщо |λ|<1, то вектор  стиснули у λ разів;
стиснули у λ разів;
якщо |λ|=1, то модуль (довжина) вектора не змінилася;
не змінилася;
якщо λ<0, то напрямок вектора a змінили на протилежний.
Отже, 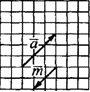 при множенні вектора
при множенні вектора  на число λ=-2/3 (тут -1< λ <0) вектор -2/3a змінив напрямок і стиснули у 2/3 рази, тобто
на число λ=-2/3 (тут -1< λ <0) вектор -2/3a змінив напрямок і стиснули у 2/3 рази, тобто 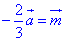 (кількість клітинок по горизонталі і вертикалі зменшили у 3 рази, а потім збільшили у 2 рази, рисунок В).
(кількість клітинок по горизонталі і вертикалі зменшили у 3 рази, а потім збільшили у 2 рази, рисунок В).
Відповідь: m – В.
Приклад 42.4 O – точка перетину медіан трикутника ABC. 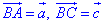
Виразити вектор OB через вектори a і c.
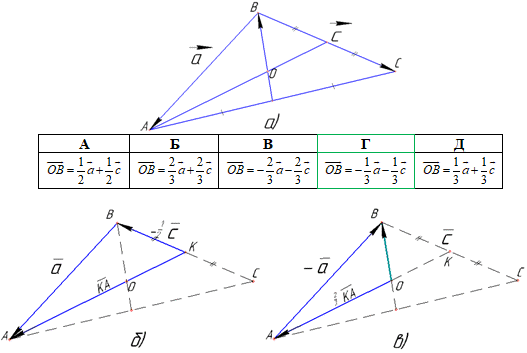
Розв'язування: Медіана AK трикутника ABC – відрізок, який виходить з вершини A трикутника і ділить протилежну сторону BC навпіл, тобто BK=KC.
Розглянемо трикутник ABK (рисунок а), у якого сторони є векторами:
BA=a, KB=-c/2 (тут BK=BC/2 і KB=-BK=-BC/2=-c/2).
За правилом трикутника додавання векторів знайдемо вектор AK:
KB+BA=KA, -c/2+a=KA, звідси KA=a-c/2.
Медіани трикутника ABC в точці перетину O діляться у відношенні 2:1, починаючи від вершини. Тобто KA=KO+OA і OA=2KO, звідси AO=2KA/3.
Розглянемо трикутник ABO (рисунок б), у якого сторони є векторами: AB=-a (протилежний до вектора a), OA=2/3•KA (за властивістю перетину медіан ΔABC).
За правилом трикутника додавання векторів знайдемо вектор OB:
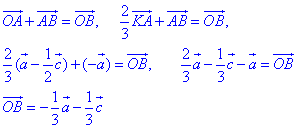
Відповідь: -1/3•a-1/3•c – Г.
Приклад 42.23 Дано квадрат ABCD. Який з наведених векторів дорівнює сумі AC+BD?
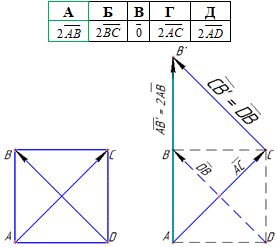
Розв'язування: У квадрата ABCD сторони і діагоналі будемо векторами із заданим напрямком позначати. Вектор DB паралельно перенесемо так, щоб його початок співпав з кінцем вектора AC, тоді отримаємо йому рівний вектор CB', тобто DB=CB' (при паралельному перенесенні напрямок і довжини векторів (їх координати) залишаються незмінними).
Додавати вектори будемо за правилом трикутника (дивись рисунок): від кінця вектора AC відкладаємо вектор DB (він же CB'), далі суму векторів отримуємо, з'єднавши початок вектора AC з кінцем вектора CB, в результаті отримаємо вектор AB' (він же 2AB, оскільки точка B перейшла в точку B' на таку ж відстань і напрямок як точку D перенесли в точку C), тобто
AC+CB'=AB', AC+DB=2AB.
Відповідь: 2AB – А.
Приклад 42.24 Вектор OA лежить на осі Oz прямокутної декартової системи координат у просторі (див. рисунок), і його початок збігається з початком координат.
Визначити координати вектора OA, якщо його довжина дорівнює 3.
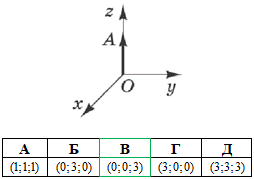
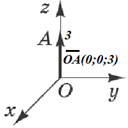
Розв'язування: За умовою завдання початок вектора OA збігається з початком координат, тому має координати O(0;0;0). Сам вектор OA лежить на осі Oz, тому його кінець, точка A, також лежить на осі Oz, тобто A(0;0;z) (на осі аплікат Oz абсциса x і ордината y дорівнюють 0).
Оскільки |OA|=3 (за умовою), то |z-0|=3, звідси z=3. Координата z>0 оскільки вектор OA напрямлений в додатному напрямку осі Oz.
Записуємо координати вектора
A(0;0;3).
Відповідь: (0;0;3). – В.
Попереду декілька статей на довжину (модуль) вектора, суми та різниці векторів, обчислення скалярного добутку та кутів між векторами. Готові приклади допоможуть Вам швидко пройти теоретичний матеріал та вивчити формули.
]]>AB(bx-ax;by-ay).
Модуль (довжина) вектора рівний кореню квадратному з суми квадратів проекцій вектора на осі
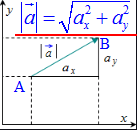
В просторі добавиться третя координати, формули аналогічні наведеним і далі їх будемо використовувати для розв'язування ЗНО тестів. В поясненнях до завдань ми не ставили знак вектора, хоча Вам це робити при розв'язуванні потрібно. За правильний приймайте запис векторів, який фігурує у формулах.
Приклад 42.14 Знайти координати вектора a, зображеного на рисунку.
|
А |
Б |
В |
Г |
Д |
|
(-3;-1) |
(2;4) |
(5;3) |
(3;-1) |
(3;1) |
Розв'язування: Початково рисунок має тільки сітку, тому дописуємо значення по осях.
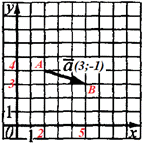
Випишемо координати початку A і кінця B вектора a:
A(2;4), B(5;3).
Запишемо координати вектора a як різницю координат кінця B(5;3) та початку A(2;4):
a(5-2;3-4)=(3;-1).
Відповідь: (3;-1). – Г.
Приклад 42.5 Дано точки A(5;-6;7) і B(8;-2;7). Знайти абсолютну величину вектора AB.
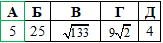
Розв'язування: Знайдемо координати вектора AB(x;y;z):
(потрібно від координат кінця B(8;-2;7) вектора AB відняти координати початку A(5;-6;7)).
AB(8-5;-2+6;7-7)=(3;4;0).
Знайдемо абсолютну величину (модуль, довжину) вектора |AB|:
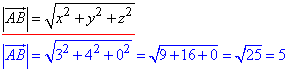
Відповідь: 5 – А.
Приклад 42.6 Знайти довжину вектора AB, якщо A(-1;1;-1) і B(-1;1;1).
|
А |
Б |
В |
Г |
Д |
|
√2 |
2 |
2√2 |
3 |
1 |
Розв'язування: Знайдемо координати вектора AB(x;y;z):
(від кінця B(-1;1;1) вектора AB віднімаємо координати початку A(-1;1;-1)).
AB(-1+1;1-1;1+1)=(0;0;2).
Знайдемо довжину (абсолютну величину) вектора |AB|:
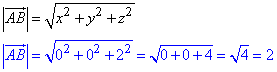
Відповідь: 2 – Б.
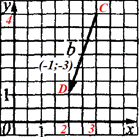
Приклад 42.15 Знайти абсолютну величину вектора b, зображеного на рисунку.
|
А |
Б |
В |
Г |
Д |
|
3 |
√3 |
√10 |
2 |
√7 |
Розв'язування: Випишемо за побудовою координати початку C і кінця D вектора b:
C(3;4), D(2;1).
Координати вектора b обчислимо як різницю координат кінця D(2;1) та початку C(3;4):
b(2-3;1-4)=(-1;-3).
Знайдемо абсолютну величину (довжину) вектора b(-1;-3):
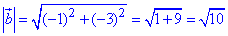
Відповідь: √10 – В.
Приклад 42.22 Знайти модуль вектора 2a+3b, якщо a(1;2), b(1;0).
|
А |
Б |
В |
Г |
Д |
|
√41 |
3 |
√17 |
1 |
9 |
Розв'язування: Перш за все побудуємо задані вектори в декартовій площині.
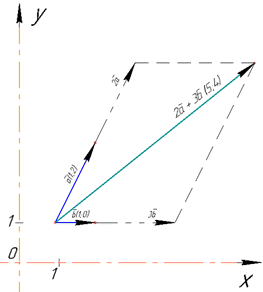
Помножити вектор на число означає помножити кожну координату на це число:
2a=(2•1;2•2)=(2;4),
3b=(3•1;3•0)=(3;0).
Додати вектори означає додати їх відповідні координати:
2a+3b=(2+3;4+0)=(5;4).
Обчислимо модуль (довжину) вектора 2a+3b:
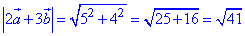
Відповідь: √41 – А.
Приклад 42.39 Дано вектор a(2;1;-3). Знайти квадрат довжини вектора b, якщо a•b=7 і вектор b колінеарний вектору a.
Розв'язування: Оскільки вектор b колінеарний вектору a(2;1;-3), то їх відповідні координати пропорційні. Нехай x – коефіцієнт пропорційності, тоді b(2x;x;-3x).
Знайдемо x з умови, що a•b=7 (скалярний добуток векторів a і b дорівнює 7):
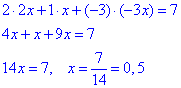
Отже, отримали b(1;0,5;-1,5).
Знайдемо квадрат довжини вектора b(1;0,5;-1,5):
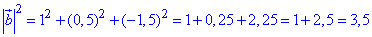 .
.
Відповідь: 3,5.
Далі підуть складніші завдання на довжину суми та різниці векторів, які вимагають знання наступних формул скалярного добутку.

Приклад 42.18 Вектори a і b утворюють кут 1350,|a|=2, |b|=2√2. Знайти |a-b|.
|
А |
Б |
В |
Г |
Д |
|
2√2 |
2√5 |
5 |
4√2 |
4 |
Розв'язування: Виконаємо схематичний рисунок векторів
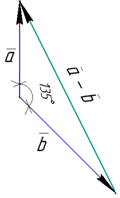
Модуль (довжина) різниці векторів |a-b| шукається за допомогою скалярного добутку векторів наступним чином:
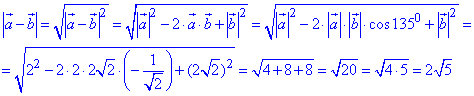
Нагадаємо правило обчислення косинуса для кутів більших від 900:
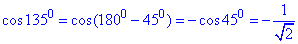
Відповідь: 2√5 – Б.
Приклад 42.19 Дві сили F1 і F2 утворюють між собою кут 1200. |F1|=|F2|=10H. Знайти модуль рівнодійної цих сил.
|
А |
Б |
В |
Г |
Д |
|
5 Н |
10 Н |
5√3 Н |
20 Н |
10√2 Н |
Розв'язування: Оскільки у математиці сили позначаються векторами, то рівнодійна двох сил F1 і F2 є векторною сумою F:
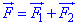
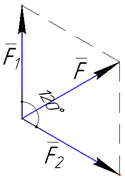
а модуль рівнодійної |F| дорівнює довжині (модулю) вектора F. Отже,
Мовою формул цьому відповідає запис
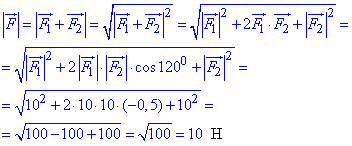
тут cos(1200) знаходимо, виходячи з періодичності косинуса
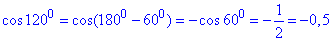
На рисунку додавання векторів (F=F1+F2) виконано за правилом паралелограма.
Відповідь: 10 Н – Б.
Приклад 42.34 Знайти довжину вектора a-b-c, якщо |a|=2, |b|=3, |c|=4, ∠(a;b)=60, ∠(b;c)=90, ∠(a;c)=120 й обчислити його значення з точністю до 0,01.
Розв'язування: Знайдемо скалярний добуток векторів a і b:
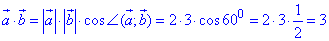
отже отримали a•b=3.
Знайдемо скалярний добуток векторів b і c:
Оскільки ∠(b;c)=90, тобто b⊥c, то b•c=0.
Знайдемо скалярний добуток векторів a і c:
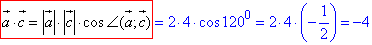 , отже отримали a•c=-4.
, отже отримали a•c=-4.
Знайдемо довжину (модуль) вектора a-b-c, який містить в собі скалярні добутки і довжини заданих векторів a, b, c:
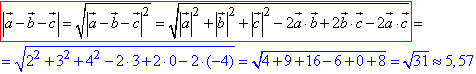
Відповідь: 5,57.
Попереду ще кілька публікацій на вектори з яких Ви дізнаєтеся схеми розв'язування прикладів на перпендикулярність та паралельність векторів, знаходження кута між векторами.
Умови перпендикулярності та колінеарності досить важливі на практиці, тому обов'язково пробіжіться по готових прикладах!
Умова колінеарності:
- два вектори колінеарні якщо пропорційні їх координати
ax/bx=ay/by=az/bz. - вектори a(a1;a2;a3) і b(b1;b2;b3) колінеарні, якщо можна знайти таке число k, що виконується відношення
b=k•a: b1=k•a1; b2=k•a2; b3=k•a3.
Основні властивості колінеарних (паралельних) векторів, які Ви повинні вивчити та знати, наведено на схемі
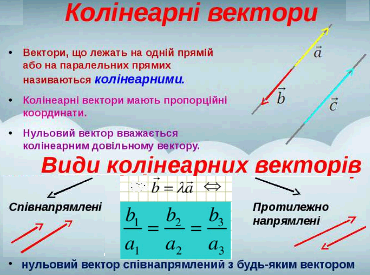
В 10,11 класі учні це вчать, ми тільки повторюємо матеріал та готуємо Вас до іспитів. Далі наведені готові розв'язки ЗНО тестів.
Для швидкого завантаження сторінок ми не ставили знак вектора, хоча при розв'язуванні потрібно. За правильний приймайте запис векторів, який фігурує у формулах.
Приклад 42.25 Установити відповідність між назвами формул для векторів a(a1;a2;a3) і b(b1;b2;b3) (1–4) та формулами (А – Д).
|
1. Довжина вектора |a| |
|
Розв'язування: У попередніх уроках всі ці формули використовувалися, тому просто випишемо їх:
1. Довжина вектора a:
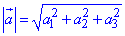 Б.
Б.
2. Формула скалярного добутку векторів (a,b):
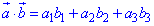 Г.
Г.
3. Умова перпендикулярності векторів a⊥b:
a⊥b, якщо 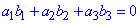 Д.
Д.
4. Умова колінеарності векторів a||b:
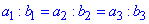 В.
В.
ЗНО 2018. Завдання 30. У прямокутній системі координат на площині задано колінеарні вектори 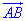 та
та 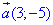 . Визначте абсцису точки B, якщо A(-4;1), а точка B лежить на прямій y=3.
. Визначте абсцису точки B, якщо A(-4;1), а точка B лежить на прямій y=3.
Розв'язування: Нехай маємо B(x;3), де x - абсциса точки B і 3 - ордината точки B, так як за умовою завдання точка B лежить на прямій y=3.
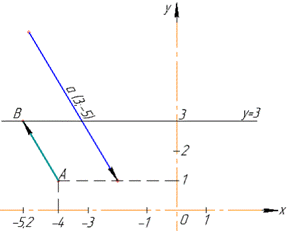
Запишемо координати вектора AB, у якого
A(-4;1): x-(-4)=x+4 - абсциса вектора 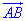 ;
;
3-1=2 - ордината вектора 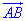 , отже
, отже 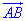 (x+4;2). Оскільки за умовою задачі вектори
(x+4;2). Оскільки за умовою задачі вектори 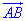 (x+4;2) та a колінеарні, то їх відповідні координати пропорційні (за властивістю):
(x+4;2) та a колінеарні, то їх відповідні координати пропорційні (за властивістю):
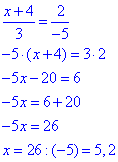
Отримали точку B(-5,2;3), де x=-5.2 абсциса точки B.
Відповідь: -5,2.
Приклад 42.7 Серед векторів a(4;14;2), b(2;7;-1), c(0;0;3), d(-6;-21;3) знайти колінеарні.
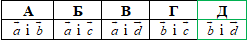
Розв'язування: Вектори колінеарні, якщо лежать на паралельних або на одній прямій. Якщо вектори колінеарні, то їх координати пропорційні!
Перевіримо колінеарність векторів a і b:
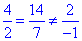
координати не пропорційні, отже вектори a і b не є колінеарними.
Перевіримо колінеарність векторів a і c:
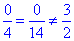
умова колінеарності не виконується, вектори a і c не є колінеарними.
Перевіримо колінеарність векторів a і d:
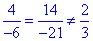
умова не виконується, вектори a і d не є колінеарними.
Перевіримо колінеарність векторів b і c:
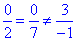 звідси вектори b і c не є колінеарними.
звідси вектори b і c не є колінеарними.
Перевіримо колінеарність векторів b і d:
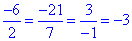
координати пропорційні, отже вектори b і d колінеарні.
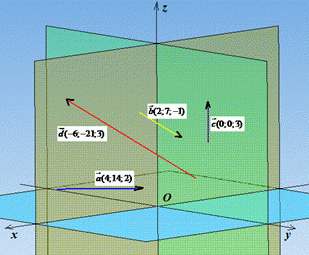
З рисунку до умови можна побачити, що лише вектори b і d паралельні. Коефіцієнт пропорційності -3 вказує на те, що вектори напрямлені в протилежну сторону і вектор d по довжині (модулю) втричі більший за вектор b.
Відповідь: b і d – Д.
Приклад 42.8 За якого значення параметра n вектори a(n+5;-8;n+1) і b(5;1-n;3) колінеарні.
|
А |
Б |
В |
Г |
Д |
|
±5 |
±5; 9 |
-9 |
5 |
5; 9 |
Розв'язування: Якщо вектори колінеарні, то їх координати пропорційні, тобто для векторів a(ax;ay;az) і b(bx;by;bz) має виконуватися умова:
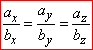
За умовою a(n+5;-8;n+1) і b(5;1-n;3) маємо
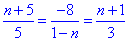
Розв’яжемо рівняння:
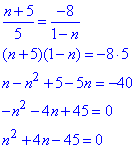
за теоремою Вієта отримаємо
n1=5, n2=-9.
Тепер перевіримо, чи отримані розв’язки задовольняють умову колінеарності з третьою координатою:
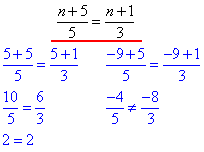
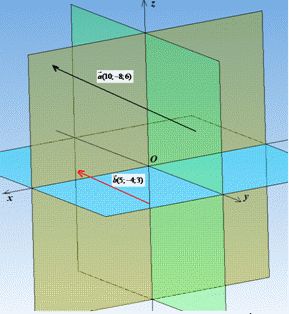
Робимо висновок, що при n=5 задані вектори a і b задовольняють умову 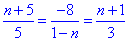 , тому їх координати пропорційні, а самі вектори a(10;-8;6) і b(5;-4;3) колінеарні. На рисунку ці вектори є паралельними.
, тому їх координати пропорційні, а самі вектори a(10;-8;6) і b(5;-4;3) колінеарні. На рисунку ці вектори є паралельними.
Відповідь: 5 – Г.
Приклад 42.36 Дано вектори a(-2;0), b(1;-1) і c(2;3).
За якого значення параметра k вектори 2a-k•b і c будуть колінеарними?
Розв'язування: Знайдемо координати вектора 2a-k•b:
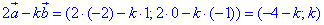
Вектори 2a-k•b і c колінеарні, якщо їх відповідні координати пропорційні:
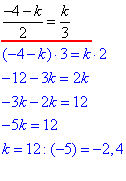
При k=-2,4 вектори 2a-k•b і c (тобто 2a-k•b=(-1,6;-2,4) і c(2;3)) будуть колінеарними.
Відповідь: -2,4.
Наведені приклади найбільш поширені, і в 10, 11 класі Ви їх проходили, принаймі мали розбирати. Попереду завдання на обчислення скалярного добутку векторів, обчислення кутів між векторами та розв'язування задач на суму та різницю векторів.
]]>Алгебраїчне означення: Скалярним добутком двох векторів a і b є скаляр (число), який рівний сумі попарних добутків проекцій векторів на осі.
Дві формули для обчислення скалярного добутку за правилами означень наведені на схемі

Далі на розгляд маємо завдання ЗНО тестів де потрібно знайти скалярний добуток.
Для оптимізації матеріалу ми не ставимо значок вектора зверху над ним, хоча це маємо на увазі. Тому правильним є запис векторів, який фігурує у формулах, Пам'ятайте про це.
Приклад 42.9 Дано вектори a(3;-6;2) і b(8;4;5). Знайти скалярний добуток a•b.
|
А |
Б |
В |
Г |
Д |
|
-17 |
0 |
-5760 |
10 |
-3 |
Розв'язування: Скалярний добуток двох векторів a(ax;ay;az) і b(bx;by;bz), заданих своїми координатами, обчислюється за формулою:
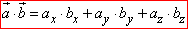 .
.
Для векторів a(3;-6;2) і b(8;4;5) отримаємо:
a•b=3•8-6•4+2•5=24-24+10=10.
Скалярний добуток більше нуля означає, що кут між заданими векторами гострий, як і показано на рисунку. Якщо кут між векторами тупий, то скалярний добуток завжди менший нуля. Знак має значення, тому Ви повинні знати за що він відповідає вскалярному добутку. Такі питання є на тестах, та й далі піде тема кути між векторами де за допомогою знаку та періодичності косинуса визначають градусну міру кутів між векторами.
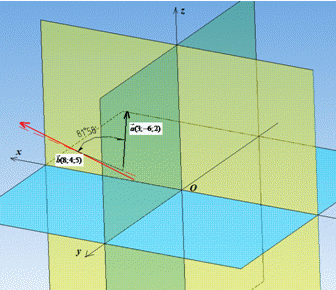
Відповідь: 10 – Г.
Приклад 42.16 Знайти скалярний добуток векторів m і n.
|
А |
Б |
В |
Г |
Д |
|
9 |
10 |
11 |
12 |
14 |
Розв'язування: Випишемо координати початку O і кінця M вектора m:
O(0;0), M(2;3).
Запишемо координати вектора m як різницю координат кінця M(2;3) та початку O(0;0):
M(2-0;3-0)=(2;3).
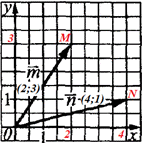
Випишемо координати початку O і кінця N вектора n:
O(0;0), N(4;1).
Запишемо координати вектора n як різницю координат кінця N(4;1) та початку O(0;0):
n(4-0;1-0)=(4;1).
Обчислимо скалярний добуток векторів m(2;3) і n(4;1):
m•n=2•4+3•1=8+3=11.
Відповідь: 11 – В.
Приклад 42.10 Обчислити квадрат довжини вектора a, якщо відомо, що він колінеарний вектору c(2;-2;3) і їх скалярний добуток дорівнює 34.
|
А |
Б |
В |
Г |
Д |
|
17 |
√17 |
2 |
4,5 |
68 |
Розв'язування: Нехай маємо вектор a(x;y;z) і колінеарний до нього вектор c(2;-2;3), тоді за властивістю колінеарності векторів отримаємо:
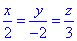
Звідси випливає, що y=-x
(випливає з рівняння x/2=-y/2) і z=1,5x (випливає з рівняння x/2=z/3).
Тому маємо a(x;-x;1,5x).
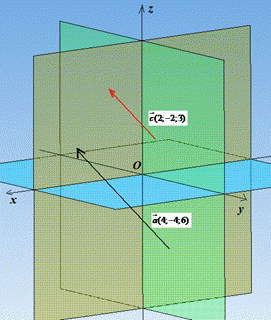
Запишемо скалярний добуток векторів a(x;-x;1,5x) і c(2;-2;3)
(за умовою a•c=34):
Запишемо скалярний добуток векторів a(x;-x;1,5x) і c(2;-2;3) (за умовою a•c=34):
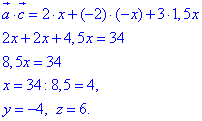
Отримали вектор a(4;-4;6). Знайдемо квадрат його довжини:
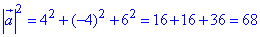 .
.
Відповідь: 68 – Д.
Приклад 42.12 Сторона рівностороннього трикутника ABC дорівнює 4. Знайти скалярний добуток векторів AB•BC.
|
А |
Б |
В |
Г |
Д |
|
8 |
-8 |
4 |
-4 |
2 |
Розв'язування: У рівностороннього трикутника ABC всі сторони рівні, тому |AB|=|BC|=4. Також всі кути рівні й дорівнюють 60 градусів (див. рисунок).
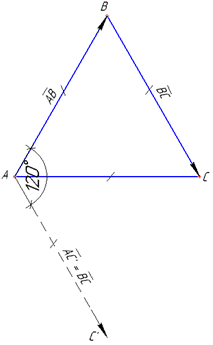
Паралельним перенесенням посунемо вектор BC у точку A, щоб вектори у цій точці мали спільний початок, тоді отримаємо вектор AC', де AC'=BC, тому
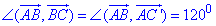 - кут між векторами AB і BC (дивись рисунок).
- кут між векторами AB і BC (дивись рисунок).
За формулою для обчислення скалярного добутку векторів (через їх довжини та кут між ними) отримаємо:
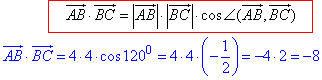
Відповідь: -8 – Б.
Приклад 42.21 Дано вектори a і b такі, що |a|=1, |b|=2, |a+b|=3. Знайти скалярний добуток векторів a і b та кут між ними.
|
А |
Б |
В |
Г |
Д |
|
1 |
2 |
4 |
6 |
8 |
Розв'язування: Такого типу завдання розв'язують методом складання рівняння.
За означенням модуля суми |a+b| і скалярного добутку a•b векторів a і b розв'язуємо
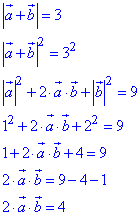
Звідси a•b=2 – скалярний добуток векторів a і b.
Розпишемо тепер a•b через добуток модулів векторів на косинус кута між ними
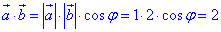
звідси виражаємо cos(φ)=1.
Косинус рівний одиниці, тому робимо висновок, що
φ=0 – кут між векторами a і b.

З рисунку можемо отримати висновок:
якщо кут між векторами рівний нулю φ=0, то |a|+|b|=|a+b|=3.
Відповідь: 2 – Б.
Приклад 42.26 Установити відповідність між векторами (1–4) та їх скалярними добутками (А–Д).
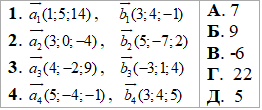
Розв'язування: Скалярний добуток векторів an(a1;a2;a3) і bn(b1;b2;b3) знаходимо за формулою:
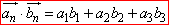 .
.
Виконуємо обчислення для 4 пар векторів та зіставлення з відповідями для тестів
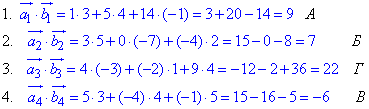
Приклад 42.30 Вектори a і b утворюють кут 120 градусів. Їх модулі рівні |a|=3,|b|=2.
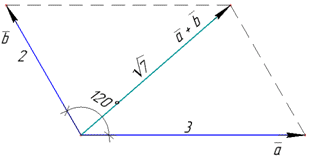
Обчислити:
1) (3a-2b)(a+2b);
2) √7|a+b|.
Розв'язування: Знайдемо скалярний добуток векторів a і b:
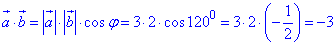 , отже отримали a•b=-3,
, отже отримали a•b=-3,
де φ=120 – кут між векторами a і b, причому
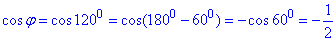
Обчислимо задані вирази, які містять в собі скалярний добуток і довжини заданих векторів a і b:
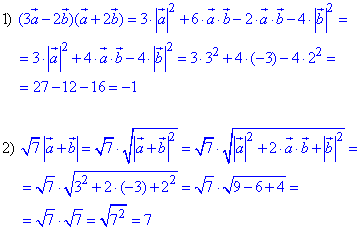
Відповідь: -1; 7.
Приклад 42.32 a(4;-2;-4), b(6;-3;2). Обчислити (2a-3b)(a-2b).
Розв'язування: Знайдемо модуль (довжину) вектора a(4;-2;-4):
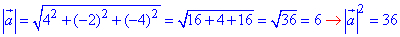
Знайдемо модуль (довжину) вектора b(6;-3;2):
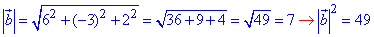
Знайдемо скалярний добуток векторів a і b:
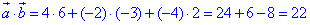
отримали a•b=22.
Обчислимо заданий вираз, який містить в собі скалярний добуток і довжини заданих векторів a і b:
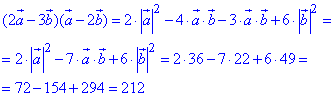
Відповідь: 212.
Приклад 42.29 Відомо, що |x|=3, |y|=6, φ=60, де φ – кут між векторами x і y.
Знайти:
1) x•(x+y);
2) √7|x+y|.
Розв'язування: Знайдемо скалярний добуток векторів x і y:
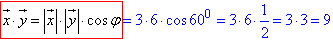
він рівний x•y=9.
Обчислимо задані вирази, які містять в собі скалярний добуток і довжини заданих векторів x і y:
1) 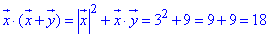
2) 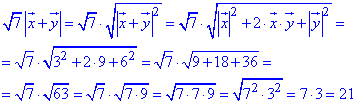
Обчислення не складні, а самі формули легко читати.
Відповідь: 18; 21.
Приклад 42.30 Дано 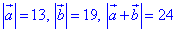 . Знайти |a-b|.
. Знайти |a-b|.
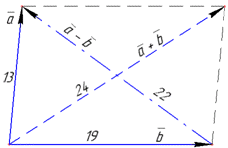
Розв'язування: З означення модуля суми векторів a і b запишемо вираз:
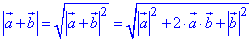
З отриманого рівняння знайдемо значення виразу 2•a•b:
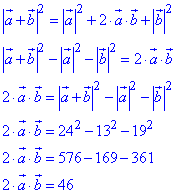
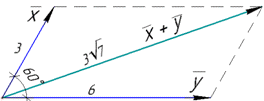
Обчислимо модуль різниці векторів a і b:
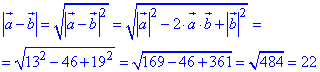
(Для звичайного паралелограма знайти довжину другої діагоналі потрібно за теоремою косинусів, або можна і методом векторів на прикладі цього завдання).
Відповідь: 22.
Приклад 42.43 На озері від пристані одночасно відпливають два катери. Один з них рухається зі швидкістю 25 км/год під кутом 300 до берега, а інший – зі швидкістю 30 км/год перпендикулярно до берега. Якою буде відстань між човнами через 6 хв? Відповідь округлити до сотих кілометра.
Розв'язування: Зробимо математичну модель задачі. Швидкість першого катера позначимо вектором a, тоді його довжина (модуль): |a|=25.
Швидкість другого катера позначимо вектором b, тоді його довжина (модуль): |b|=30.
Напрями векторів a і b зображаємо згідно умовою задачі, як показано на рисунку.
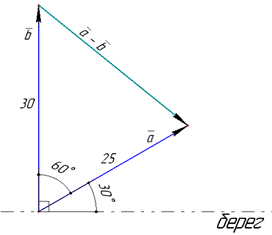
Через деякий час після початку руху катерів швидкість їх буде змінюватися, але вектор швидкості одного катера відносно іншого катера дорівнюватиме різниці векторів обох катерів, тобто a-b, де кут між векторами a і b дорівнює 600 (див. рисунок).
Обчислимо скалярний добуток векторів a і b, де кут між векторами дорівнює 600 (див. рисунок):
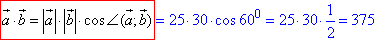
Знайдемо довжину (модуль) вектора a-b:
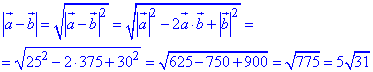
Звідси швидкість одного катера відносно іншого рівна v=5√31 км/год.
Знайдемо відстань s між човнами через 6 хв руху з точністю до сотих кілометра, причому спершу слід перетворити час з хвилин в години
t=6 хв=6/60 год=0,1 год:
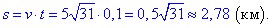
Відповідь: 2,78.
Далі йдуть задачі на умову перпендикулярності та обчислення кута через скалярний добуток.
]]>Умова перпендикулярності

Якщо вектори перпендикулярні, то їх скалярний добуток a•b=0 рівний нулю:
ax•bx+ay•by+az•bz=0.
Інша умова, що також вимагає обчислення скалярного добутку полягає в тому, що косинус кута між перпендикулярними векторами рівний нулю
cos(phi)=0.
Розглянемо завдання на ознаку перпендикулярності.
Приклад 1. Чи перпендикулярні вектори?
1. a(-2;3;0), b(6;4;-11);
2. c(-8;5), d(1;7).
Розв'язання:Обчислюємо скалярний добуток векторів a,b:
a•b=-2•6+3•4+0•(-11)=0.
Вектори перпендикулярні a⊥b, оскільки їх скалярний добуток рівний нулю.
Перевіримо другу пару векторів, обчислимо скалярний добуток
c•d=-8•1+5•7=27.
Робимо висновок, що вектори c,d не перпендикулярні, оскільки ознака перпендикулярності не виконується
c•d=27≠0.
Далі розглянемо тести із ЗНО підготовки, де потрібно перевірити умову перпендикулярності.
Приклад 42.11 При якому значенні x вектори a(2;x) і b(-4;10) перпендикулярні?
|
А |
Б |
В |
Г |
Д |
|
-5 |
-0,8 |
0,8 |
5 |
20 |
Розв'язування: Вектори a(2;x) і b(-4;10) будуть перпендикулярними (a⊥b), якщо їх скалярний добуток дорівнюватиме нулю:
a•b=0.
З умови перпендикулярності a•b=2•(-4)+x•10=0 обчислюємо параметр x:
-8+10x=0,
10x=8,
x=8:10=0,8.
В декартовій площині вони мають вигляд
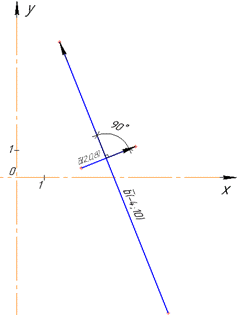
Відповідь: 0,8 – В.
Приклад 42.27 Установити відповідність між значеннями числа x (1–4), та парами векторів (А–Д), які за цих значень взаємно перпендикулярні.
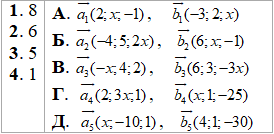
Розв'язування: Умова перпендикулярності векторів an(a1;a2;a3) і bn(b1;b2;b3):
a⊥b, якщо a1b1+a2b2+a3b3=0.
Для кожної пари векторів обчислюємо скалярний добуток векторів і прирівнюємо його до нуля. Отримане рівняння розв'язуємо відносно "ікс"
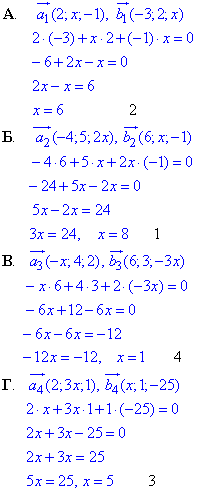
Записуємо відповідь до тестів:
1 – Б, 2 – А, 3 – Г, 4 – В.
На ЗНО тестах такі завдання поширені, тому запам'ятайте алгоритм обчислень.
Приклад 42.20 a і b – ненульові вектори. |a+b|=|a-b|. Знайти кут між векторами a і b.
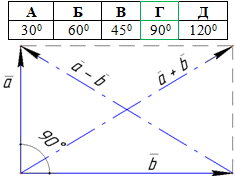
Розв'язування: В умові рисунку немає, його виконано на основі всіх розрахунків.
Нехай φ – кут між векторами a і b, виписуємо модуль суми та різниці векторів.
Далі прирівнявши довжини, складаємо рівняння для знаходження кута між векторами
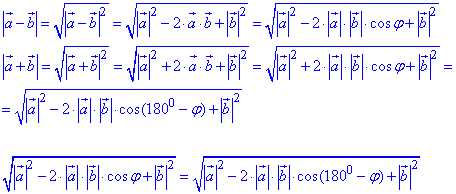
Підносимо до квадрату та спрощуємо подібні доданки
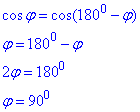
Робимо висновок, що якщо |a+b|=|a-b|, то кут між векторами a і b дорівнює 90 градусів.
З рисунка добре видно, що при побудові суми (a+b) і різниці (a-b) векторів за правилом паралелограма отримали прямокутник, у якого (за властивістю) діагоналі є рівними (|a+b|=|a-b|).
Відповідь: 900 – Г.
Приклад 42.37 Знайти площу паралелограма, побудованого на векторах AB(3;0;-4) і AD(0;5;0).
Розв'язування: Знайдемо скалярний добуток векторів AB(3;0;-4) і AD(0;5;0):
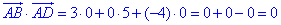
він рівний нулю.
Це означає, що вектори перпендикулярні AB⊥AD і паралелограм ABCD є прямокутником.
Знайдемо модуль (довжину) вектора AB(3;0;-4):
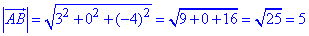
Знайдемо модуль (довжину) вектора AD(0;5;0):
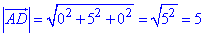
Оскільки у прямокутника дві сусідні сторони рівні, то він є квадратом. Знайдемо площу заданого паралелограма (квадрата) ABCD:
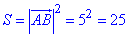
Відповідь: 25.
Скалярний добуток обчислюють через досить просту формулу, тому великого різноманіття прикладів на умову перпендикулярності Ви не знайдете. Спробуйте обчислити кілька завдань самостійно, Ви побачите, що тема не важка для вивчення. Набагато важчими в плані розрахунків є завдання на обчислення довжини суми чи різниці векторів, обчислення площ чи об'ємів тіл побудованих на векторах, але це вже інша тема.
]]>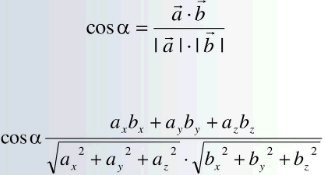
Верхня формула це векторний запис, нижня в координатній формі для просторових (тримірних) векторів.
Далі розглянемо приклади із ЗНО тестів на обчислення косинуса кута, та встановлення його градусної міри. Порядок розрахунків кута легко прослідкувати з наведених далі готових розв'язків. Завдання в першу чергу підійдуть учням 10-11 класів, останні приклади будуть повчальними і для студентів.
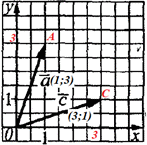
Приклад 42.17 Обчислити косинус кута між векторами a і c.
|
А |
Б |
В |
Г |
Д |
|
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
Розв'язування: Випишемо координати початку O і кінця A вектора a:
O(0;0), A(1;3).
Обчислимо координати вектора a як різницю координат кінця A(1;3) та початку O(0;0):
A(1-0;3-0)=(1;3).
Обчислимо довжину (модуль) вектора a(1;3):
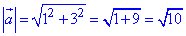
Такі ж операції проводимо для вектора с:
O(0;0), C(3;1).
Координати вектора c знаходимо через різницю координат кінця C(3;1) та початку O(0;0):
c(3-0;1-0)=(3;1).
Через корінь квадратний з суми квадратів координат знаходимо довжину (модуль) вектора c(3;1):
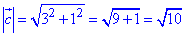
Скалярний добуток векторів a(1;3) і c(3;1):
a•c=1•3+3•1=6.
Обчислимо косинус кута φ між векторами a(1;3) і c(3;1) за формулою:
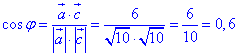
Відповідь: 0,6 – Д.
Приклад 42.13 Знайти кут між векторами a(1;0;-1) і b(0;-1;1).

Розв'язування: Кут φ між векторами a і b знайдемо за формулою:
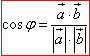
Обчислимо скалярний добуток векторів:
a•b=1•0+0•(-1)+(-1) •1=-1.
Визначимо довжину (модуль) векторів a,b:
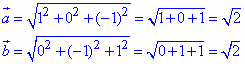
Знайдемо косинус кута φ між векторами a і b:
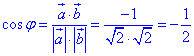
Визначимо кут φ між векторами через арккосинус:
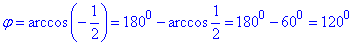
Отримали тупий кут в 120 градусів.
Відповідь: 1200 – Б.
Приклад 42.33 Дано |m|=2, |n|=3, а кут між векторами m і n дорівнює 120 градусів. Обчислити косинус кута між векторами m і m+n і знайти його значення з точністю до 0,01.
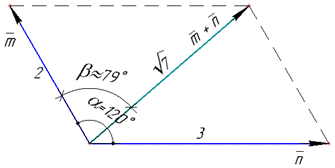
Розв'язування: Знайдемо скалярний добуток векторів m і n:
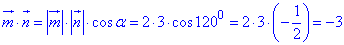 , отже отримали m•n=-3,
, отже отримали m•n=-3,
де α=120 – кут між векторами m і n, причому
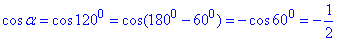
Знайдемо модуль (довжину) вектора m+n:
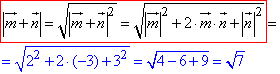
отже |m+n|=√7.
Знайдемо скалярний добуток векторів m і m+n:
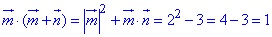
Обчислимо косинус кута β між векторами m і m+n, знайдемо його значення з точністю до 0,01:
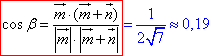
та сам кут β=arccos(0,19)=79.
Відповідь: 0,19.
Приклад 42.35 Знайти косинус кута між векторами -5a і 1/5•b з точністю до 0,01, якщо a(-1;1;4), b(1;0;-1).
Розв'язування: Знайдемо координати векторів -5a і 1/5•b:
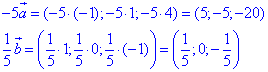
Знайдемо скалярний добуток векторів -5a і 1/5•b:
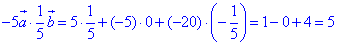 , отже отримали a•b=5.
, отже отримали a•b=5.
Знайдемо модуль (довжину) вектора -5a:
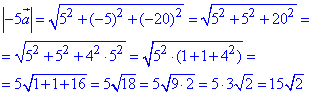
маємо|-5a|=15√2.
Знайдемо модуль (довжину) вектора 1/5•b:
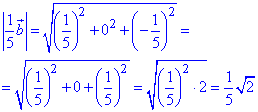
Знайдемо косинус кута φ між векторами -5a і 1/5•b з точністю до 0,01:
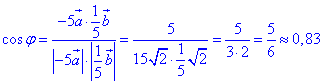
звідси φ=arccos(0,83)≈340.
Відповідь: 0,83.
Приклад 42.38 Дано трикутник MPK з вершинами в точках M(3;-2), P(1;4), K(2;-1). Знайти у градусах величину кута M.
Розв'язування: Знайдемо координати вектора MP:
MP=(1+3;4+2)=(4;6).
Знайдемо довжину (модуль) вектора MP(4;6):
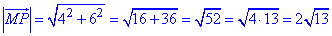
Знайдемо координати вектора MK:
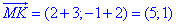
Знайдемо довжину (модуль) вектора MK(5;1):
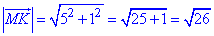
Знайдемо скалярний добуток векторів MP(4;6) і MK(5;1) рівний 26:
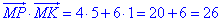
Обчислимо косинус кута M, тобто косинус кута між векторами MP і MK:
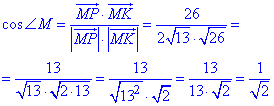
далі величину кута M через arccos():
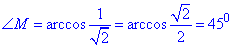
Побудуємо трикутник на трьох заданих векторах
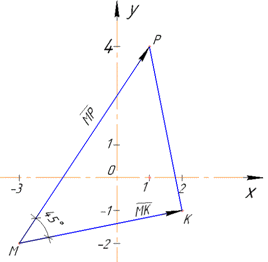
Відповідь: 45 градусів.
Приклад 42.40 Дано модулі двох векторів та кут між ними
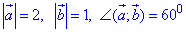
Знайти косинус кута між векторами a+b і a-b з точністю до 0,01.
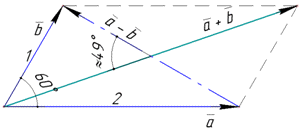
Розв'язування: Завдання ускладнюється тим що тут потрібно розраховувати модулі та скалярні добутки суми та різниці векторів, а для цього потрібно вивести більш складні формули. Уважно перегляньте хід обчислень, та запам'ятайте що для чого тут робили.
Визначимо скалярний добуток векторів a і b:
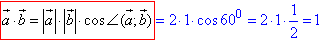
Довжину суми векторів a+b обчислимо за формулою:
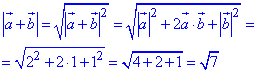
Модуль різниці векторів a-b знаходимо за правилом:
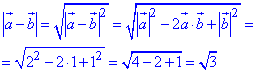
Скалярний добуток векторів a+b і a-b обчислимо за формулою різниці квадратів:
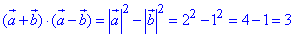
Знаходимо косинус кута φ між векторами a+b і a-b з точністю до сотих:
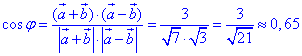
Знаючи що cos(φ)=0,65, на калькуляторі можемо визначити сам кут
φ=arccos(0,65)≈490.
Відповідь: 0,65.
Приклад 42.41 Знайти косинус кута між діагоналями паралелограма, побудованого на векторах a(3;2) і b(1;-2) з точністю до 0,01.
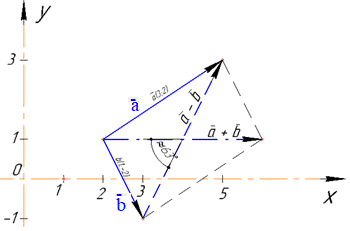
Розв'язування: Діагоналями паралелограма, побудованого на векторах a і b (згідно з правилом додавання і віднімання векторів) будуть вектори a+b і a-b.
Визначаємо координати вектора a+b:
a+b=(3+1;2-2)=(4;0).
З рисунку бачимо, оскільки вектор a+b має координати (4;0), то цей вектор розташований паралельно осі абсцис (Ox).
Знайдемо довжину a+b:
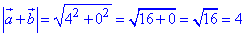
Координати вектора a-b:
a-b=(3-1;2+2)=(2;4).
Обчислюємо довжину (модуль) вектора a-b:
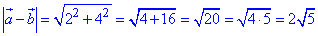
Скалярний добуток векторів a+b і a-b рівний різниці квадратів:
(a+b)(a-b)=4•2+0•4=8.
Знаходимо косинус кута φ між діагоналями паралелограма (векторами a+b і a-b) з точністю до сотих:
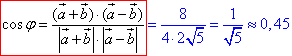
звідси φ=arccos(0,45)≈630.
Відповідь: 0,45.
Приклад 42.42 Знайти косинус кута між діагоналями паралелограма, побудованого на векторах a=4m+2n і b=4m+n з точністю до 0,01, якщо |m|=|n|=1, φ=∠(m;n)=60.
Розв'язування: Для ілюстрації, що шукаємо та який вигляд мають вектори на площині наведемо рисунок
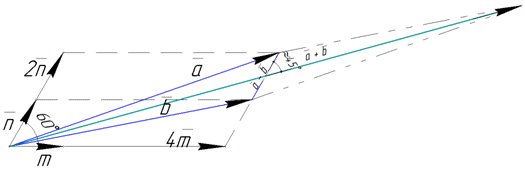
Діагоналями паралелограма, побудованого на векторах a і b (згідно з правилом додавання і віднімання векторів) будуть вектори a+b і a-b, де
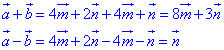
Знайдемо скалярний добуток векторів m і n:
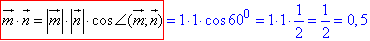
Знайдемо модуль суми векторів a+b=8m+3n:
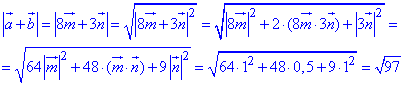
Знайдемо модуль вектора a-b=n:
|a-b|=|n|=1.
Обчислимо скалярний добуток векторів a+b=8m+3n і a-b=n:
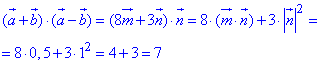
Визначимо косинус кута α між діагоналями паралелограма (векторами a+b і a-b) з точністю до сотих:
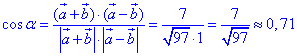
звідси α=arccos(0,71)≈450.
Відповідь: 0,71.
Попереду ще сотні готових відповідей із ЗНО підготовки, тому вчіться та економте грошенята на репетиторах.
Додавайте сайт в закладки та діліться з друзями у соцмережах!
Приклад 41.1 Точки A(2;-4;-8) і B(10;-20;6) симетричні відносно точки C. Знайти координати точки C.
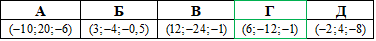
Розв'язування: Щоб Ви могли з легкістю розуміти всі текстові пояснення до формул, нами виконані допоміжні рисунки до завдань.
Це допоможе доказати (нехай і візуальна) ряд теорем та властивостей, які Ви повинні знати з теоретичного матеріалу. Плюс це Вам багато допоможе в навчанні і читанні формул.
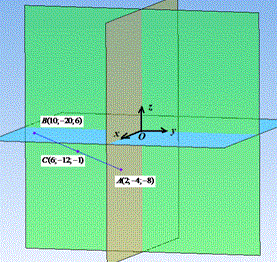
Якщо точки A(2;-4;-8) і B(10;-20;6) симетричні відносно точки C, то це означає, що точка C є серединою відрізку AB.
За формулою 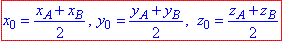 знайдемо координати середини відрізка AB.
знайдемо координати середини відрізка AB.
(Якщо відрізок знаходиться у площині xOy, то третя координата z відсутня).
Виконуємо обчислення
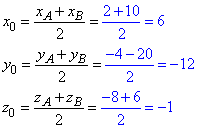
C(6;-12;-1) - координати шуканої точки C.
Відповідь: (6;-12;-1) – Г.
Приклад 41.2 На координатній площині xOy зображене коло, центр якого збігається з початком координат (див рисунок). Точки K(8;6) і M(x;y) належать колу. Визначте координати точки M.
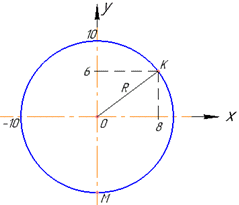
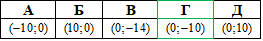
Розв'язування: Знайдемо радіус R кола як відстань між точками O(0;0) (початок координат, центр кола) і K(8;6) (точкою на колі).
 - відстань між точками O і K (довжина OK відрізка ) на площині xOy.
- відстань між точками O і K (довжина OK відрізка ) на площині xOy.
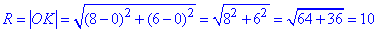
Відрізки OK і OM рівні як радіуси кола (OK=OM=R=10), тому точка M має координати (0;-10), оскільки належить колу і від’ємній півосі ординат Oy, тобто M(0;-10).
Відповідь: (0;-10) – Г.
Приклад 41.3 Дано трикутник ABC, вершини якого мають координати A(-2;6), B(-2;2) і C(4;-2). Знайти довжину медіани BM.
|
А |
Б |
В |
Г |
Д |
|
2 |
3 |
4 |
5 |
6 |
Розв'язування: Медіана трикутника - відрізок, який виходить з вершини трикутника і ділить протилежну сторону навпіл, тобто AM=MC (див.рис.).
Знайдемо координати середини відрізка AC, тобто координати точки M:
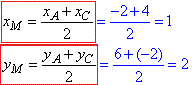
звідси M(1;2).
Знайдемо довжину відрізка (медіани) BM - відстань між точками B і M за формулою:
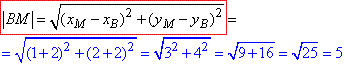
Відповідь: 5 – Г.
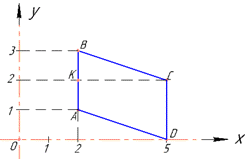
Приклад 41.4 Обчислити площу чотирикутника ABCD (див. рисунок), сторони AB і CD якого паралельні осі Oy.
|
А |
Б |
В |
Г |
Д |
|
10 |
5 |
3 |
6 |
7 |
Розв'язування: Оскільки AB||Oy і CD||Oy (звідси AB||CD), то заданий чотирикутник ABCD – трапеція з основами
|AB|=|yB-yA|=|3-1|=2 і |CD|=|yD-yC|=|0-2|=2.
Проведемо відрізок CK||Ox, звідси CK⊥AB, тому відрізок CK– висота трапеції ABCD.
За формулою площі трапеції через добуток середньої лінії на висоту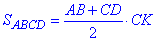 отримаємо
отримаємо
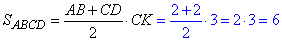
ІІ – спосіб.
Можна довести, що заданий чотирикутник ABCD – паралелограм. Тому за формулою площі паралелограма SABCD=AB•CK отримаємо
SABCD=AB•CK=2•3=6.
Відповідь: 6 – Г.
Приклад 41.5 Знайти координати точки, яка симетрична точці A(1;2;3) відносно площини xOy.
Розв'язування: Якщо точка B(x;y;z) симетрична точці A(1;2;3) відносно площини xOy, то координати абсциси x і ординати y обох точок співпадають, а координата аплікати z змінює свій знак на протилежний, отже точка B(1;2;-3) симетрична точці A(1;2;3) відносно площини xOy. Щоб мати уявлення як це виглядає в просторі до цього та наступних завдань побудовані зрізи 3d рисунків. З них Вам стане ясно чому так є, та загалом хід викладених міркувань.
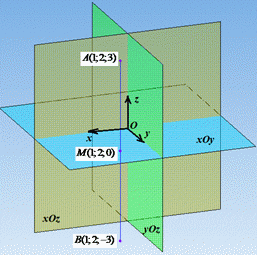
Точка M(1;2;0) є серединою відрізка AB і належить площині xOy (точки A і B симетричні відносно точки M).
Відповідь: (1;2;-3) – Д.
Приклад 41.6 Знайти координати точки, яка симетрична точці A(10;20;30) відносно осі аплікат.
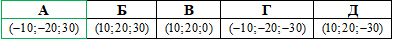
Розв'язування: Якщо точка B(x;y;z) симетрична точці A(10;20;30) відносно осі аплікат (осі Oz), то координати аплікати z обох точок співпадають, а координати абсциси x і ординати y змінюють свій знак на протилежний, отже точка B(-10;-20;30) симетрична точці A(10;20;30) відносно осі аплікат (осі Oz).
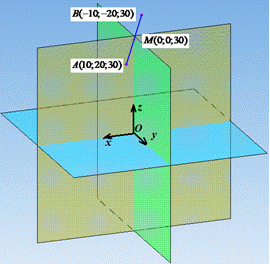
Точка M(0;0;30) є серединою відрізка AB і належить осі Oz (точки A і B симетричні відносно точки M).
Відповідь: (-10;-20;30) – А.
Приклад 41.7 При паралельному перенесенні точка A(1;2;6) переходить у точку A1(6;7;0). Вказати координати точки, у яку при цьому переходить точка B(7;9;1).
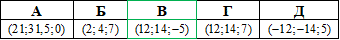
Розв'язування: Знайдемо координати вектора 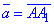 , при якому здійснюється паралельне перенесення з точки A(1;2;6) в точку A1(6;7;0):
, при якому здійснюється паралельне перенесення з точки A(1;2;6) в точку A1(6;7;0):
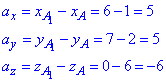
Напрямний вектор рівний 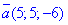 . Наведемо просторовий рисунок до завдання
. Наведемо просторовий рисунок до завдання
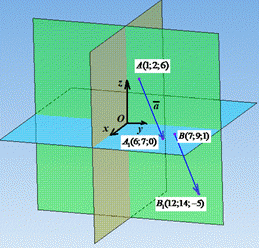 Знайдемо координати точки B1(x;y;z), у яку переходить точка B(7;9;1) при паралельному перенесенні на вектор
Знайдемо координати точки B1(x;y;z), у яку переходить точка B(7;9;1) при паралельному перенесенні на вектор 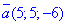 :
:
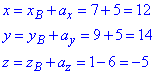
Записуємо у вигляді B1(12;14;-5).
Відповідь: (12;14;-5) – В.
Приклад 41.8 Знайти відстань від точки M(5;4;12) до осі ординат.
|
А |
Б |
В |
Г |
Д |
|
5 |
4 |
12 |
13 |
21 |
Розв'язування: Відстань від точки до прямої (в просторі) – це перпендикуляр опущений з точки на пряму.
Проведемо перпендикуляр MA до площини xOy і поставимо точку A(5;4;0), проведемо перпендикуляр AB до площини yOz (до осі Oy) і поставимо точку B(0;4;0). 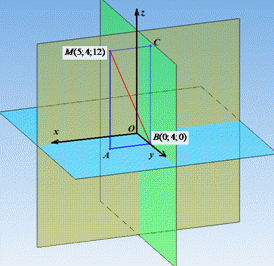
Проведемо похилу MB до площини xOy, тоді AB її проекція на цю площину. Оскільки AB⊥Oy, то за теоремою про три перпендикуляри BM⊥Oy, тому відрізок MB - відстань від точки M(5;4;12) до осі ординат.
Точка A(5;4;0) має такі координати, оскільки відрізок (перпендикуляр) MA опущений з точки M(5;4;12) паралельно осі Oz на площину xOy (тому абсциса і ордината не змінилися, а у площині xOy апліката z дорівнює нулю).
Точка B(0;4;0) має такі координати, оскільки відрізок (перпендикуляр) AB опущений з точки A(5;4;0) паралельно осі Ox на вісь Oy (тому ордината не змінилася, а на осі Oy абсциса x і апліката z дорівнюють нулю).
Знайдемо відстань між точками M(5;4;12) і B(0;4;0)за формулою:
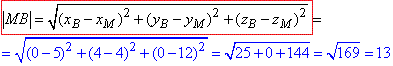
(Інша схема обчислень відрізка MB слідує із прямокутного трикутника ΔMAB за темою «35 прямі та площини в просторі», але тут показано метод координат).
Відповідь: 13 – Г.
Приклад 41.9 Знайти відстань від точки P(3;-6;8) до площини yOz.
|
А |
Б |
В |
Г |
Д |
|
3 |
4 |
6 |
8 |
10 |
Розв'язування: Відстань від точки до площини (в просторі) – це перпендикуляр опущений з точки на площину.
Проведемо перпендикуляр PK до площини yOz (паралельно вісі Ox) і поставимо точку K(0;-6;8), тут ордината і апліката не змінилися, а у площині yOz абсциса x дорівнює нулю.
Уважно погляньте на рисунок нижче, щоб переконатися в цьому.
Довжина відрізка PK і буде відстанню від точки P(3;-6;8) до площини yOz.
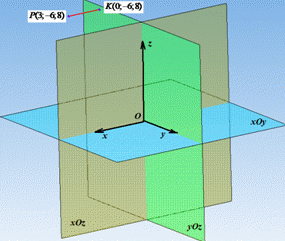
Знайдемо довжину відрізка PK: P(3;-6;8) і K(0;-6;8),

(Якщо відрізок паралельний деякій осі координат, то модуль різниці координат точок по цій осі й буде довжиною відрізка).
Відповідь: 3 – А.
В наступній статті навчимося складати рівняння кола, сфери, зводити їх рівняння до канонічного вигляду, знаходити радіус.
]]>Приклад 41.10 Скласти рівняння сфери, яка проходить через початок координат із центром у точці S(-1;2;-3).
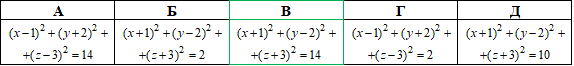
Розв'язування: Маємо точку на сфері, яка співпадає з центром координат і сам центр сфери. Побудуємо просторовий рисунок до завдання
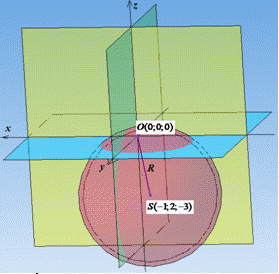
Рівняння сфери з центром у точці S(a;b;c) і радіусом R:
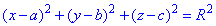
З умови відомо a=-1, b=2 і c=-3.
Оскільки точка S(-1;2;-3) - центр сфери, а точка O(0;0;0) (початок координат) належить сфері, то |OS|=R, звідси |OS|2=R2, обчислимо:
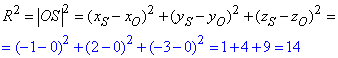
Отже, рівняння сфери має вигляд
(x+1)^2+(y-2)^2+(z+3)^2=14.
Відповідь: (x+1)2+(y-2)2+(z+3)2=14 – В.
Приклад 41.11 Вказати рівняння кола, яке на площині симетричне до кола (x-4)^2+(y+5)^2=9 відносно осі Oy.
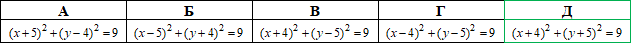
Розв'язування: Рівняння кола з центром у точці (a;b) і радіусом r:
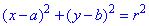
Маємо коло (x-4)2+(y+5)2=9 з центром A(4;-5) і радіусом r=3.
Якщо задане коло симетрично відобразити відносно осі Oy, то абсциси координат точок кола (та його центра) зміняться на протилежні, а ординати і геометричні розміри (радіус, довжина кола) залишаться без змін. Це добре видно з наступного рисунка кіл
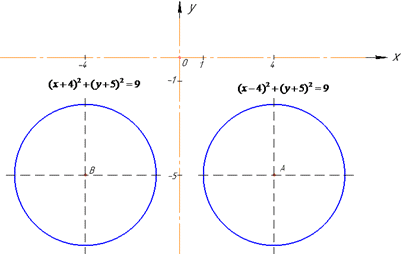
Тому при симетрії відносно осі Oy заданого кола отримаємо коло з центром B(-4;-5) та радіусом r=3.
Складаємо рівняння симетричного осі кола:
(x+4)2+(y+5)2=9.
Відповідь: (x+4)^2+(y+5)^2=9 – Д.
Приклад 41.12 Скласти рівняння кола з центром у точці C(5;-2), яке дотикається до осі ординат.
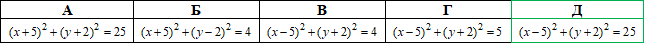
Розв'язування: Почнемо з теорії та пригадаємо, що рівняння кола з центром у точці (a;b) і радіусом r має запис:
(x-a)^2+(y-b)^2=r^2.
За умовою: a=5, b=-2.
Схематичний рисунок до завдання приведено далі
Радіус r знайдемо з умови, що задане коло дотикається до осі ординат (Oy). Оскільки в точці дотику радіус кола перпендикулярний до дотичної, то з цього випливає, що точка дотику кола до осі Oy має координати (0;-2) (абсциса x на осі ординат дорівнює нулю, а ордината дотику дорівнює ординаті центру кола).
Звідси отримуємо довжину радіуса кола: r=|5-0|=5 (тобто r=|x|=5, r^2=25).
Отже, рівняння заданого кола має вигляд:
(x-5)^2+(y+2)^2=25.
Відповідь: (x-5)^2+(y+2)^2=25 – Д.
Приклад 41.13 Скласти рівняння сфери з центром у точці A(-1;3;2), яке дотикається до площини xOy.
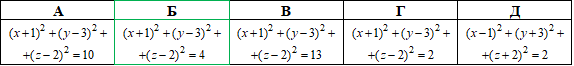
Розв'язування: Запишемо рівняння сфери з центром у точці A(a;b;c) і радіусом R:
(x-a)^2+(y-b)^2+(z-c)^2=R^2.
Рисунок сфери з площинами є підказкою до обчислень
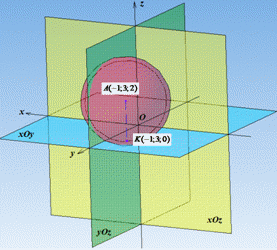
Радіус R знайдемо з умови, що задана сфера дотикається до площини xOy.
Оскільки в точці дотику радіус сфери перпендикулярний до дотичної, то з цього випливає, що точка дотику сфери з площиною xOy має координати (-1;3;0) (абсциса x і ордината y на площині xOy залишаються без змін, такі як у центра сфери, а апліката дотику z рівна нулю).
Базуючись на цьому можемо визначити радіус сфери:
R=|2-0|=2 (тобто R=|z|=2, R^2=4).
Складаємо рівняння сфери за вказаною на початку формулою:
(x+1)2+(y-3)2+(z-2)2=4.
Відповідь: (x+1)^2+(y-3)^2+(z-2)^2=4 – Б.
Приклад 41.14 Знайти координати центра кола x2-4x+y2+10y+20=0.
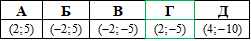
Розв'язування: Зведемо задане рівняння кола x^2-4x+y^2+10y+20=0 до канонічного вигляду (методом виділення повних квадратів):
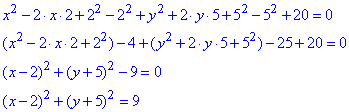
(x-2)^2+(y+5)^2=3^2.
Отримали канонічне рівняння кола (вигляду (x-a)^2+(y-b)^2=r^2), з якого маємо
A(2;-5) - координати центра кола, r=3 - радіус кола.
Наведемо рисунок досліджуваного кола в декартовій площині
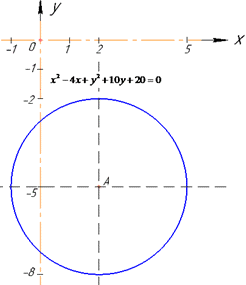
Відповідь: (2;-5) – Г.
Приклад 41.15 Знайти радіус сфери x2+y2-2y+z2+6z-6=0.
|
А |
Б |
В |
Г |
Д |
|
2 |
3 |
4 |
5 |
6 |
Розв'язування: Такого типу завдання полягають у зведенні до канонічної форми (методом виділення повних квадратів) самого рівняння сфери x^2+y^2-2y+z^2+6z-6=0, що само по соб не складно. Права частина тоді рівна квадрату сфери, а координати центра заховані в дужках.
Проведемо необхідні перетворення рівняння:
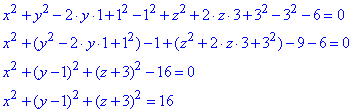
x^2+(y-1)^2+(z+3)^2=4^2.
Отримали канонічне рівняння сфери (вигляду (x-a)^2+(y-b)^2=r^2)), з якого маємо S(0;1;-3) - координати центра сфери, R=4 - радіус сфери.
Рисунок сфери має вигляд
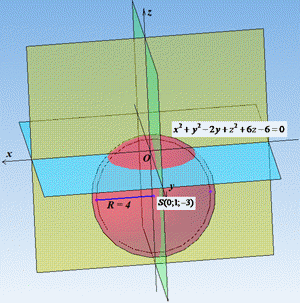
Відповідь: 4 – В.
Приклад 41.29 Знайти: 1) радіус R сфери;
2) площу S сфери (у відповідь записати S/π), заданої рівнянням x2+y2+z2-2x+2y-2=0.
Розв'язування: Зведемо задане рівняння сфери x^2+y^2+z^2-2x+2y-2=0 до канонічного виду (методом виділення повних квадратів):
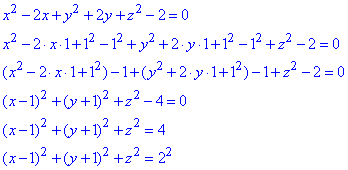
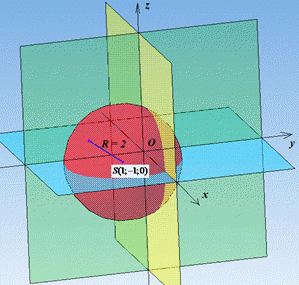
Вивели канонічне рівняння сфери (вигляду (x-a)^2+(y-b)^2+(z-c)^2=R^2), з якого маємо S(1;-1;0) - координати центра сфери, R=2 - радіус сфери.
Знайти площу S сфери допоможе формула:
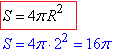
звідси S/π=16π/π=16.
Відповідь: 2; 16.
Приклад 41.30 Скласти рівняння кола з центром на осі ординат, яке проходить через точки A(-3;0), B(0;9). У відповідь записати довжину радіуса кола.
Розв'язування: Точка S - центр заданого кола, яке лежить на осі ординат (Oy), тому S(0;y).
Побудуємо допоміжний рисунок до завдання
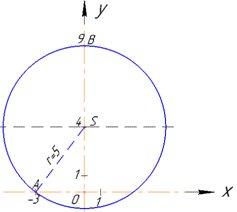
Оскільки задане коло проходить через точки A(-3;0), B(0;9), то |AS|=|BS|=r як радіуси кола (відстані від точки S(0;y) до точок A(-3;0) і B(0;9) відповідно), звідси |AS|2=|BS|2.
Складаємо рівняння квадратів модулів векторів
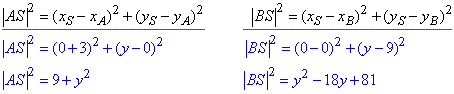
Прирівнявши останні дві залежності, знайдемо ординату y центра кола:
9+y^2=y^2-18y+81,
18y=81-9=72,
y=72:18=4.
S(0;4) - центр заданого кола.
Знайдемо його радіус r з умови (|AS|=|BS|=r):
r2=(|AS|2=9+42,
r^2=25,
r=5.
Будуємо рівняння кола :
(x-0)^2+(y-4)^2=5^2, або
x2+(y-4)2=25.
На цьому задача розв'язана, уважно перегляньте хід обчислень, адже такого типу завдань у Вас в навчанні буде багато.
Відповідь: 5.
Приклад 41.23 Установити відповідність між центрами і радіусами сфер (1–4) та їх рівняннями (А–Д). 
Розв'язування: Канонічне рівняння сфери має вигляд:
(x-a)^2+(y-b)^2+(z-c)^2=R^2, де C(a;b;c) - координати центра сфери;
R - радіус сфери.
У кожному з наведених завдань підставимо координати центра та радіус сфери у канонічне рівняння, розкриємо дужки і зведемо подібні доданки.
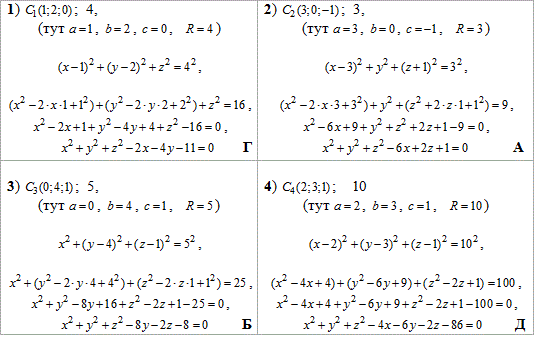
Розрахунки не складні, і всі деталі перетворень легко простежити з наведеної таблиці.
Задачі на знаходження координат точок, канонічних рівнянь кіл, сфер, обчислення відстані на площині та в просторі Ви повинні навчитися швидко та правильно розв'язувати, щоб успішно скласти ЗНО тести, вступні іспити та не мати проблем з навчанням у ВУЗах. Попереду ще дві публікації з готовими відповідями до задач на координати.
]]>Приклад 41.16 Дано ABCD – паралелограм з трьома вершинами A(-4;1;5), B(-5;4;2), C(3;-2;-1). Знайти координати вершини D.
Розв'язування: Для відшукання четвертої вершини скористаємося властивістю про те, що у паралелограма ABCD діагоналі AC і BD в точці перетину (S) діляться навпіл:
AS=SC, BS=SD. Схематичний рисунок паралелограма має вигляд
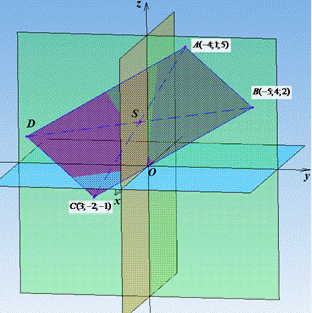
Спочатку знайдемо координати центра S - середини відрізка (діагоналі) AC за відомими координатами:
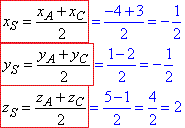
Отримали 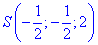 - координати точки перетину діагоналей AC і BD.
- координати точки перетину діагоналей AC і BD.
Із умови, що BS=SD складаємо рівняння для знаходження координати точки D і розв'язуємо:
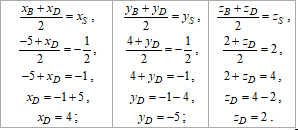
D(4;-5;2) - шукана вершина.
Відповідь: (4;-5;2) – Д.
Приклад 41.17 Дано ABCDA1B1C1D1 – куб. A(7;0;0), B(5;0;0),C1(5;2;2). Знайти координати вершини D1.
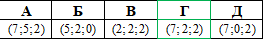
Розв'язування:Обчислення проведемо по аналогічній схемі з попереднім завданням: за відомими вершинами визначимо центр куба як середину між точками, а далі складемо рівняння за відомою вершиною центром для обчислення D1.
У куба ABCDA1B1C1D1 діагоналі AC1 і BD1 (всі його діагоналі) в точці перетину (S) діляться навпіл:
AS=SC1, BS=SD1.
Рисунок до задачі має вигляд
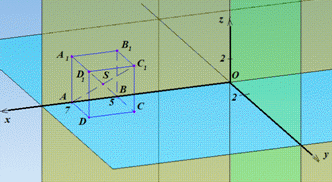
Спочатку знайдемо координати точки S - середини відрізка (діагоналі) AC1:
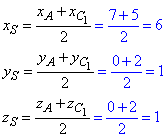
Звідси, S(6;1;1) - координати точки перетину діагоналей AC1 і BD1.
Із умови, що BS=SD1 складемо 3 рівняння для знаходження координати вершини D1:
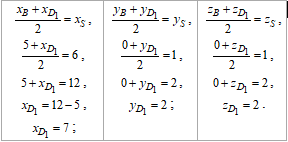
Шукана вершина куба має координати D1(7;2;2).
Додатково, із умови координат точок A(7;0;0), B(5;0;0), C1(5;2;2) - деяких вершин куба ABCDA1B1C1D1 помічаємо, що його сторони паралельні осям координат, тому інші вершини куба матимуть координати:
A1(7;0;2), B1(5;0;2), C(5;2;0), D(7;2;0).
Вчіть зауважувати подібні аналогії з побудови та координатного запису, часто це спрощує хід розрахунків.
Відповідь: (7;2;2) – Г.
Приклад 41.18 Дано трикутник ABC з вершинами A(2;2;-4), B(2;-1;-1), C(3;-1;-2). Знайти зовнішній кут при вершині B.
|
А |
Б |
В |
Г |
Д |
|
60 |
90 |
120 |
135 |
інша відповідь |
Розв'язування: Схема обчислень полягає у знаходженні косинуса кута через скалярний добуток двох векторів, що виходять з однієї вершини трикутника.
Для цього зі сторін трикутника ABC сформуємо вектори:
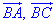 зі спільним початком при вершині B.
зі спільним початком при вершині B.
Рисунок трикутника в просторі має вигляд
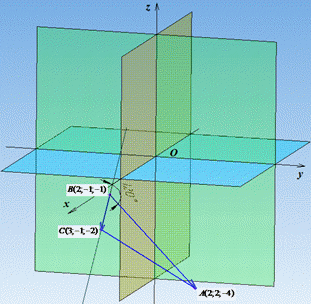
Знайдемо координати ВА, ВС:
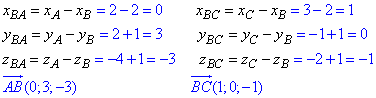
Обчислимо скалярний добуток векторів за формулою
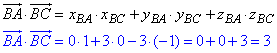
Знайдемо модулі (довжини) векторів BA і BC:
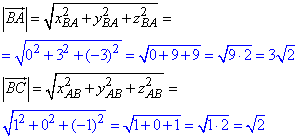
Маючи довжини між точками, знайдемо косинус кута між векторами BA і BC - внутрішній кут B трикутника ABC за формулою:
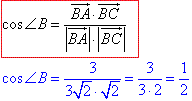
Косинус рівний 0,5, отже робимо висновок що кут рівний ∠B=60.
Знайдемо зовнішній кут при вершині B (за означенням зовнішнього кута трикутника):
180-∠B=180-60=120.
(В цьому завданні було використано метод векторів у просторі, який детально розглядатиметься у розділі 42).
Відповідь: 120 – В.
Приклад 41.19 Точки A(2;4) і C(5;8) є вершинами квадрата ABCD. Знайти площу цього квадрата.
|
А |
Б |
В |
Г |
Д |
|
2,5 |
5 |
12,5 |
25 |
20 |
Розв'язування: У квадрата ABCD відрізок AC називається діагоналлю. Виконаємо допоміжний рисунок до завдання
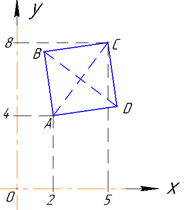
Площу квадрата ABCD можна обчислити за формулою:
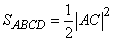
Її без проблем можете знайти онлайн або вивести через сторони квадрата.
Обчислимо квадрат довжини відрізка (діагоналі) AC:
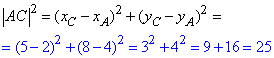
Знайдемо площу квадрата ABCD:
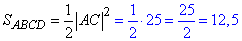
Відповідь: 12,5 – В.
Приклад 41.20 Точки A(-1;0;2) і B(0;1;1) є вершинами правильного трикутника. Знайти площу цього трикутника.
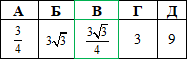
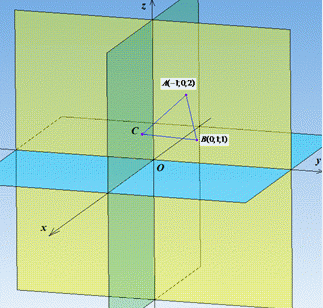
Розв'язування: У правильного (рівностороннього) ΔABC всі сторони рівні:
|AB|=|AC|=|BC|.
Тому, площу трикутника ABC можна обчислити за формулою:
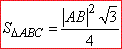
Визначимо квадрат довжини відрізка (сторони) AB із залежності:
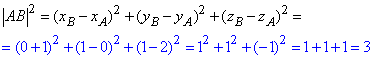
Знайдемо площу правильного трикутника ABC:
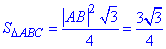
Серед варіантів тестів вірний результат містить пункт В.
Відповідь: 3√3/4 – В.
Приклад 41.22 При паралельному перенесенні точка A(1;3;2) переходить у точку A'(3;0;1). Установити відповідність між точками (1–4) та точками (А–Д), утвореними при цьому паралельному перенесенні.

Розв'язування: Обчислимо координати вектора 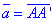 , при якому здійснюється паралельне перенесення з точки A(1;3;2) в точку A'(3;0;1):
, при якому здійснюється паралельне перенесення з точки A(1;3;2) в точку A'(3;0;1):
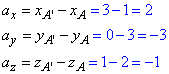
Остаточно, a(2;-3;-1).
Знайдемо координати точок M’(x;y;z), у яку переходять точки Mn при паралельному перенесенні на вектор a(2;-3;-1):

Обчислення під силу школярам і полягають в додаванні до координат заданих вершин координат вектора AA'.
(Завдання повністю аналогічне до завдання Приклад 41.7, тому рисунки не наводимо).
Приклад 41.24 Установити відповідність між парами точок (1–4), та відстанями між цими точками (А–Д).

Розв'язування: Відстань між точками M і N (довжина відрізка MN) в просторі знаходимо за формулою:

Послідовно для кожного пункту тестів підставляємо координати та виконуємо обчислення:
1) M1(1;3;4), N1(2;1;2)
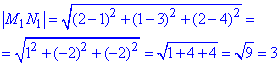 А;
А;
2) M2(3;5;1), N2(0;1;1)
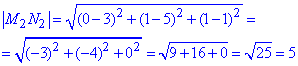 В;
В;
3) M3(-2;3;4), N3(6;3;-2)
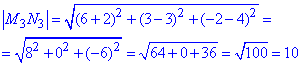 Д;
Д;
4) M4(1;-2;5), N4(1;10;0)
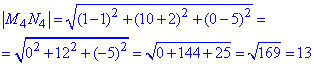 Б.
Б.
В тестах добре, що підказкою є варіанти відповідей. Тому, якщо отримали якесь друге значення, то скоріш за все допустили помилки в обчисленнях.
Вивчайте та запам'ятовуйте формули, без яких Ви не зможете вирішити задач в координатах.
Приклад 41.21 d(x) – відстань від точки M(x;0;0) до площини yOz. Який з наведених графіків є графіком функції d=d(x)?
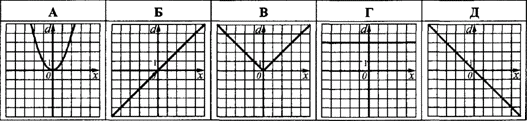
Розв'язування: Точка M(x;0;0) належить осі Ox і приймає будь-яке її значення, ордината y та апліката z при цьому дорівнюють 0.
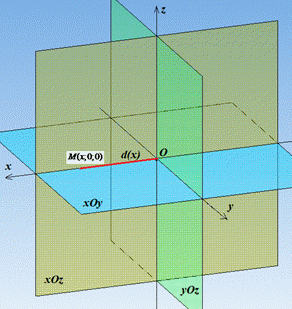
Звідси слідує, що відстань від точки M(x;0;0) до площини yOz дорівнює модулю абсциси цієї точки, тобто
d(x)=|x|.
Серед запропонованих в тестах відповідей слід обрати ту, яка містить графік модуль функції. Такий варіант зображений на рисунку В.
Відповідь: В.
Приклад 41.25 На осі ординат знайти ординату точки, рівновіддаленої від точки A(-4;2) і початку координат.
Розв'язування: Побудуємо схематичний рисунок до задачі
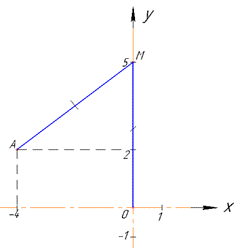
Нехай M(0;y) - точка на осі ординат (Oy), ординату y якої потрібно знайти.
Оскільки точка M(0;y) рівновіддалена від точки A(-4;2) і точки O(0;0) (початку координат), то |AM|=|OM| (довжини відрізків AM та OM рівні), відповідно рівні квдрати модулів
|AM|2=|OM|2.
Обчислюємо довжини векторів
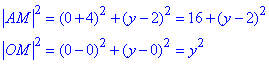
Прирівняємо дві останні рівності та з отриманого рівнянння виразимо невідому y:
16+(y-2)^2=y^2,
16+y^2-4y+4=y^2,
-4y=-20,
y=20:4=5.
Запам'ятайте схему обчислень до завдання.
Точка M з координатами (0;5) рівновіддалена від точки A(-4;2) і початку координат.
Відповідь: 5.
Приклад 41.26 Скласти рівняння прямої, яка проходить через точку M(-2;5) й утворює з додатним напрямом осі абсцис кут 45 градусів. У відповідь записати абсцису точки перетину прямої з віссю абсцис.
Розв'язування: Рівняння прямої на площині має вид: y=k•x+b,
де k - кутовий коефіцієнт нахилу прямої до осі абсцис (Ox);
k=tg(φ),
φ - кут нахилу прямої з додатнім напрямом осі абсцис, за умовою φ=45;
b - ордината перетину прямої з віссю ординат (Oy).
Обчислюємо кутовий коефіцієнт k=tg(45)=1.
Наведемо рисунок прямої під кутом 45 градусів до осі абсцис.
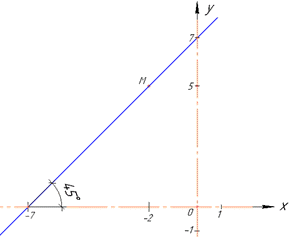
Щоб знайти параметр b підставимо координати точки M(-2;5) (тут x=-2 і y=5) і значення k=1 у загальне рівняння прямої:
5=1•(-2)+b,
5=-2+b,
b=5+2=7.
Отримали таке рівняння прямої y=x+7.
При y=0 знаходимо
x=-7 - абсцису точки перетину прямої з віссю абсцис (Ox).
Відповідь: -7.
Приклад 41.27 Знайти:
1) площу трикутника;
2) периметр трикутника, обмеженого осями координат і прямою 4x+3y=24.
Розв'язування: Знайдемо координати трикутника AOB, сторонами якого є осі координат і пряма 4x+3y=24.
Наперед наведемо рисунок трикутника, який досліджуємо
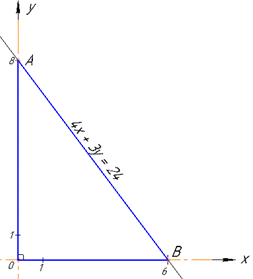
Вершина O(0;0) - початок координат, кут при цій вершині дорівнює 90 тому ΔAOB - прямокутний з катетами AO і OB, гіпотенузою AB.
Вершина A(0;y) належить осі ординат (Oy).
З умови перетину прямої 4x+3y=24 з віссю ординат (x=0) знайдемо ординату точки A:
4•0+3y=24,
3y=24,
y=24:3=8
Отже, A(0;8) - координати вершини A, звідси слідує, що катет AO=8. Такі пояснення потрібні, оскільки нам не тільки потрібно знайти координати вершин трикутника, а й визначити відстані між вершинами, після чого обчислити периметр та площу трикутника.
Вершина B(x;0) належить осі абсцис (Ox).
З умови перетину прямої 4x+3y=24 з віссю абсцис (y=0) знайдемо абсцису точки B:
4x+3•0=24,
4x=24,
x=24:4=6.
Отже, B(6;0) - координати вершини B, звідси слідує, що катет OB=6.
Гіпотенузу (довжину вдрізка) AB знайдемо як відстань між точками A(0;8) і B(6;0):
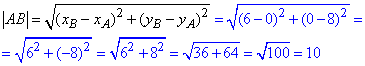
(як бачимо на виході все одно отримали запис звичайної теореми Піфагора).
Отже, AB=10 - довжина гіпотенузи прямокутного ΔAOB.
Знаходимо площу прямокутного трикутника ΔAOB через півдобуток основи на висоту:
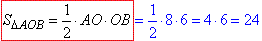
Обчислимо периметр трикутника ΔAOB:
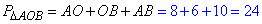
Відповідь: 24; 24.
Приклад 41.28 Знайти квадрат довжини медіани AA1 трикутника ABC, якщо A(3;-2;1), B(3;1;5) і C(4;0;3).
Розв'язування: Медіана AA1 трикутника ABC ділить сторону BC навпіл, тобто BA1=A1C.
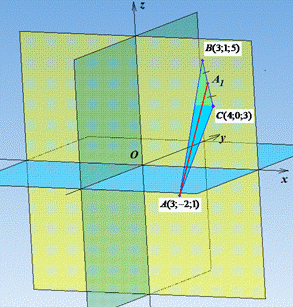
Для знаходження координати точки A1 - середини відрізка (сторони) BC застосуємо формулу:
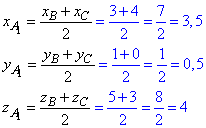
Остаточно A1(3,5;0,5;4).
Знайдемо квадрат довжини медіани AA1 як квадрат відстані між точками A(3;-2;1) і A1(3,5;0,5;4):
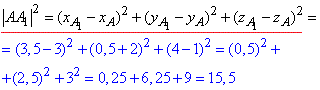
Ось такі розрахунки Ви маєте вміти виконувати, щоб легко скласти вступні іспити у ВУЗи.
Відповідь: 15,5.
Приклад 41.31 Точка M(2;6;3) - середина відрізка, кінці якого лежать на осі Ox і на площині yOz. Знайти довжину відрізка.
Розв'язування: Завдання досить складне для школярів, що погано уявляють собі прямі та ін. в просторі. В умові достатньо підказок, щоб вирішити завдання, і в цьому зараз переконаєтеся (див. рисунок).
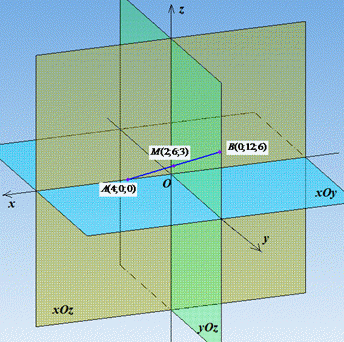
Нехай точка A один кінець відрізка, який лежить на осі абсцис (Ox), тоді її координати A(xA;0;0) (на осі Ox ордината y і апліката z дорівнюють нулю).
Нехай точка B інший кінець відрізка, який лежить на площині yOz, тоді її координати B(0;yB;zB) (на площині yOz абсциса x дорівнює нулю).
Отримали відрізок AB, серединою якого є точка M(2;6;3).
Знайдемо координати кінців A(xA;0;0) і B(0;yB;zB) відрізка AB з формули про середню точку:
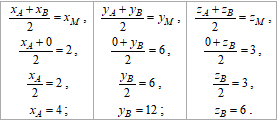
Знайшли A(4;0;0) і B(0;12;6) - координати кінців відрізка AB.
Обчислимо довжину відрізка AB як відстань між точками A(4;0;0) і B(0;12;6):
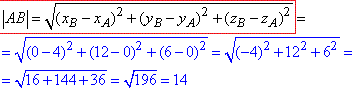
Запам'ятайте цю формулу, нею часто доводиться користуватися в задачах на координати.
Відповідь: 14.
Приклад 41.32 На ділянці, яка обмежена з двох боків взаємно перпендикулярними дорогами, посадили сад. Відстань від яблуні до першої дороги становить 3м, а до другої – 4м. Відстань від груші до першої дороги дорівнює 6м, а до другої – 8 м.
Знайти відстань між цими деревами.
Розв'язування: Зробимо математичну модель задачі. Ділянку разом з дорогами замінимо на систему координат, осями якої будуть дороги. Початок координат буде точка перетину доріг (дороги за умовою перпендикулярні). Дерева, що ростуть у саду замінимо на точки, зокрема, яблуню позначимо як точку A, а грушу – як точку B.
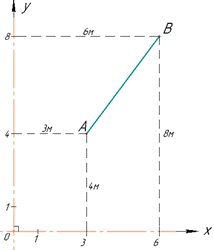
Першу дорогу позначимо за вісь ординат (Oy), а другу дорогу – за вісь абсцис (Ox). Відповідні відстані від дерев до доріг і будуть координатами точок A(3;4) і B(6;8) (дивись рисунок).
Знайдемо відстань між точками A(3;4) і B(6;8) – довжину відрізка AB:
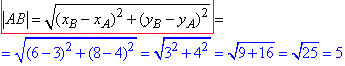
Шукана відстань між деревами 5м.
Ще раз перегляньте пояснення до цієї задачі та попередніх та зацініть, наскільки добре мати просторову уяву і вміння розбивати складні завдання на прості дії.
Відповідь: 5.
Якщо маєте цікаві завдання, які розкривають не описані тут алгоритми розв'язування прикладів на координати, то діліться з нами. Ми їх красиво оформимо та опублікуємо!
]]>