Тригонометричними називають рівняння, в яких невідома величина знаходиться під тригонометричними функціями sin(), cos(), tg(), ctg() та їх всеможливими комбінаціями. Також тригонометричними називають рівняння в яких присутні обернені тригонометричні функції arcsin(), arccos(), arctg(), arccctg().
Розв'язати тригонометричне рівняння означає звести його до найпростішого типу, а далі визначити множину розв'язків. В даному курсі буде наведена методика аналітичного обчислення тригонометричних рівнянь. Вона годиться для навчання, оскільки Ви вдосконалюєте знання тригонометричних функцій та вивчаєте різні схеми зведення рівнянь до найпростішого типу. Для інженерів і практиків більш швидкий графічний метод, який полягає у побудові двох функцій з рівняння та уточнення коренів у необхідному інтервалі числовими методами.
Далі наведені відповіді до прикладів з підготовки до зовнішнього незалежного оцінювання (ЗНО). Потібні умови завдань Ви можете зустріти під час навчання у ВУЗ-ах при навчанні на математичних дисциплінах.
Завдання 18.1 Розв'язати рівняння 2sin(x)=-1.
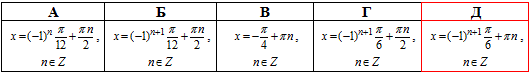
Розв'язання: Перепишемо рівняння 2sin(x)=-1, sin(x)=-1/2.
Звідси аргумент рівний
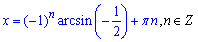
або після підстановки значення арксинуса
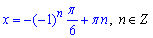
Остаточно отримаємо
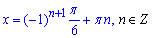
Якщо sin(x)=a і -1≤a≤1, то маємо розв'язок:

Відповідь: Д.
Додатково наведемо графічний розв'язок рівняння 2sin(x)=-1.
Його можна отримати в MATLAB, MathCAD, Maple та багатьох інших поширених математичних пакетах.
В середовищі MATLAB код скрипта для виводу графіків синуса та прямої наступний
clear;
x=-pi/2:pi/50:2*pi;
y2=sin(x);
y1(1:126)=-1/2;
figure (1), plot(x,y2,'r');
hold on;
plot(x,y1,'b');
xlim([-pi/2,2*pi]);
legend('sin(x)','-1/2');
set(gca,'Xtick',-pi:pi/6:4*pi);
grid on;
Тут одразу нанесли сітку по осі Ох кратну Пі/6, щоб переконатися, що при підставленні n=0 в формулу дістанемо x=-Pi/6=-0,5236, при n=1 маємо x=Pi+Pi/6=3,6652, при n=2 x=2Pi-Pi/6. Точки перетину двох функцій і є шуканими розв'язками тригонометричного рівняння
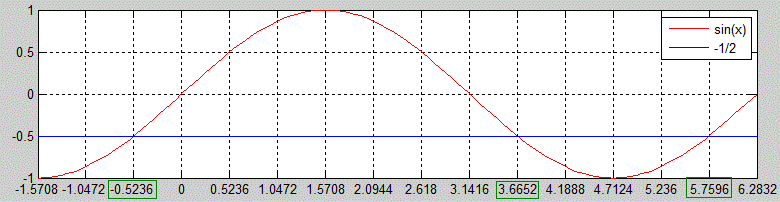
Графічний метод розв'язання рівнянь не завжди дає змогу записати аналітичний вираз коренів, зате красиво ілюструє що собою являє рівняння, а в задачах на кількість коренів на проміжку дає можливість швидко встановити значення. Звуженням інтервалу показу графіка та розбиттям сітки можна добитися доброї точності розв'язку.
Плюсом графічного методу є те що не кожне тригонометричне рівняння можна вирішити аналітично, а от графічно - завжди.
Завдання 18.2 Розв'язати рівняння sin(Pi*x)=1.
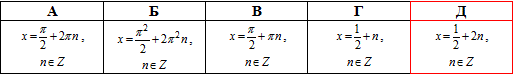
Розв'язання: З висновку попереднього завдання для рівняння sin(Pi•x)=1 можемо записати розв'язок
Pi•x=Pi/2+2Pi•n, або після нормування аргументу у виді
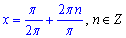
Після скорочення на Pi дробів отримаємо
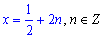
Для рівняння sin(x)=-1 розв'язок матиме вигляд:
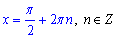
Відповідь: Д.
Оскільки маємо вже один раз написаний скрипт в MATLAB, то злегка будимо його модифіковувати під задане і всі наступні рівняння.
Після заміни сітки та функцій на потрібні код має вигляд
clear;
x=-pi/2:pi/50:2*pi;
y2=sin(pi*x); % замінили функцію на нову
y1(1:126)=1; % нова права частина =1
figure (1), plot(x,y2,'r');
hold on;
plot(x,y1,'b');
xlim([-pi/2,2*pi]);
legend('sin(Pi*x)','1');
set(gca,'Xtick',-2:1/2:4*pi); % поміняли сітку на кратну 0,5
grid on;
В результаті отримали графік потрібної синусоїди та прямої (вгорі синя лінія), точки перетину є шуканими коренями р-ня.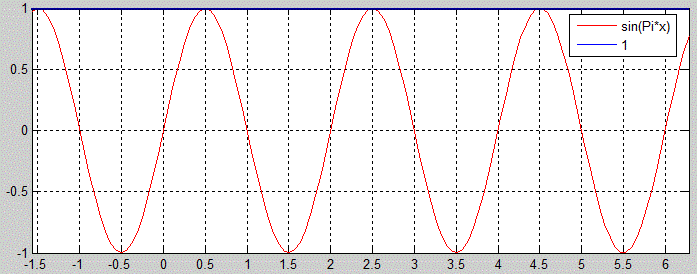
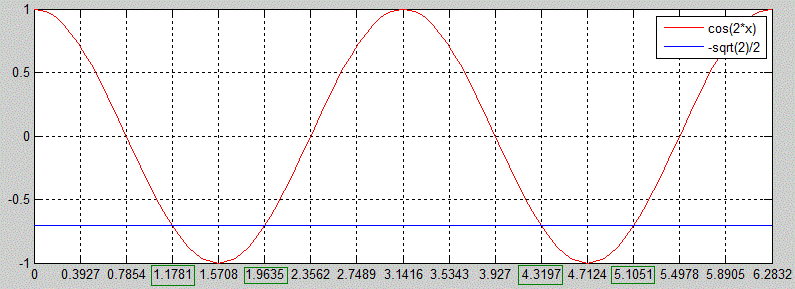
Завдання 18.3 Розв'язати рівняння 2cos(2x)=- √2.
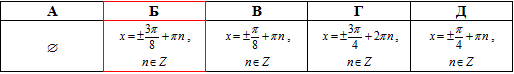
Розв'язання: Перетворимо рівняння до правильного виду
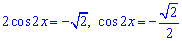
звідси
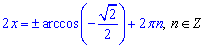
або після підстановки арккосинуса через кут
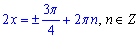
Після спрощення на двійку отримаємо відповідь
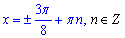
Розв'язок можна узагальнити на випадок будь-якої правої частини рівняння з косинусом:
Якщо cos(x)=a і -1≤a≤1, то маємо розв'язок:
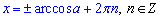
Заданому інтервалу належить значення

Відповідь: Б.
Скрипт в матлабі модифікуємо для рівняння cos(2x)=-√2/2 .
Цього разу будували на проміжку [0,2Pi] з сіткою по осі "іксів" кратною Pi/8.
clear;
x=0:pi/50:2*pi;
y2=cos(2*x);
y1(1:101)=-sqrt(2)/2;
figure (1), plot(x,y2,'r');
set(gca,'Xtick',-pi:pi/8:2*pi);
hold on;
plot(x,y1,'b');
xlim([0,2*pi]);
legend('cos(Pi*x)','2^(0.5)/2');
grid on;
Графік подвійного косинуса та правої частини рівняння наступні:
Завдання 18.4 Розв'язати рівняння √3tan(x+Pi/6)=1.
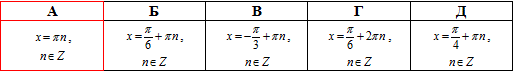
Розв'язання: Перенесемо корінь з трійки в праву частину рівняння
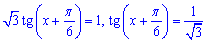
звідси
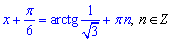
Після підстановки арктангенса розв'язок матиме вигляд
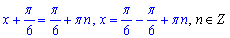
Остаточно отримаємо
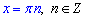
Запишемо узагальнений корінь рівняння:
Якщо tan(x)=a, то маємо розв'язок:
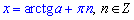
Відповідь: А.
Графічно тангенс та пряму отримаємо при компіляції коду:
clear;
x=-pi/2:pi/50:2*pi;
y2=tan(x+pi/6);
y1(1:126)=1/sqrt(3);
figure (1), plot(x,y2,'r');
hold on;
plot(x,y1,'b');
xlim([-pi/2,2*pi]);
ylim([-6,6]);
legend('tan(x+pi/6)','1/sqrt(3)');
set(gca,'Xtick',-pi:pi/2:2*pi);
grid on;
Тут ввели обмеження по осі "ігрик" до +-6, оскільки тангенс приймає великі значення в околі асимптот, що може негативно позначитися на видимості прямої y=1/√3.
Графічне розв'язання тригонометричного рівняння наведене далі
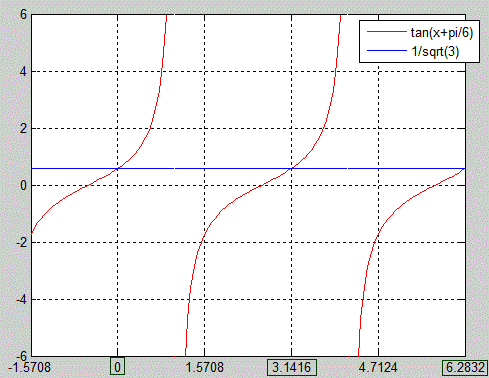
Завдання 18.5 Розв'язати рівняння 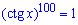 .
.
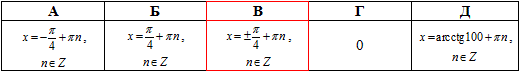
Розв'язання: Спершу може здатися, що таке показникові рівняння надто складне. Але варто представити праву частину у тому ж степені і обчислення спрощуються
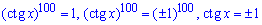
Звідси 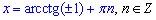
Після підстановки арккотангенса корінь рівняння рівний
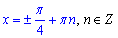
Тут врахували, що арккотангенси для одиниці та мінус одиниці рівні між собою
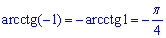
Якщо в іншому випадку це не справдиться то корені рівняння необхідно зшивати або об'єднувати.
Узагальнений розв'язок для рівняння з котангенсом має вигляд:
Якщо ctg(x)=a, то маємо розв'язок:
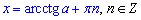
Відповідь: В.
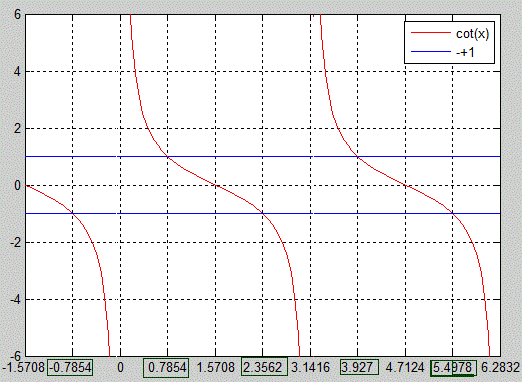
Наведемо лише рядки, які змінилися з попереднього завдання для побудови функцій y=ctg(x), y=1:
y2=cot(x);
y1(1:126)=1;
legend('cot(x)','1');
set(gca,'Xtick',-pi:pi/4:2*pi);
Тут графічно котангенс прирівняли до плюс мінус одиниці та встановили нижню сітку кратну Pi/4.
Завдання 18.6 Указати рівняння, яке має хоча б один корінь.
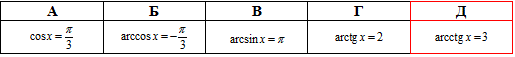
Розв'язання: Рівняння cos(x)=Pi/3 не має коренів, оскільки Pi/3≈1,05>1 (при 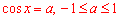 ).
).
Рівняння arcos(x)=-Pi/3 не має коренів, тому що –Pi/3<0 (при 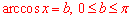 ).
).
2 р-ня arcsin(x)=Pi не має коренів, бо суперечить ОДЗ: Pi>Pi/2 (при 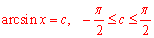 ).
).
3 р-ня arctg(x)=2 не має коренів, тому що виходить за межі ОДЗ: 2>Pi/2 (при 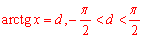 ).
).
Рівняння arcctg(x)=3 має хоча б один корінь, оскільки задовільняє ОДЗ: 0<3(при 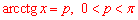 ).
).
Відповідь: Д.
Подібних прикладів можна навести десятки, і вони за складністю не надто відрізнятимуться від наведених.
Решта відповідей до 40 тригонометричних рівнянь буде розглянуто в наступних публікаціях.
На Вас ще чекають вкладені рівняння, р-ня з параметром та тригонометричні р-ня 4 порядку.


