Приклади розв'язання тригонометричних рівнянь

Продовжуємо аналізувати відповіді до 50 прикладів із підготовки до зовнішнього незалежного оцінювання. Одночасно з класичним визначенням розв'язків тригонометричних рівнянь наведемо код для Matlab або Maple, щоб побудувати функції з рівняння. Точки перетину кривих і будуть шуканими розв'язками. Переваги такої методики розв'язання читайте у попередній публікації.

Приклад 18.7 Указати рівняння, яке має тільки один корінь.

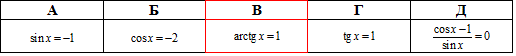
Розв'язання: Рівняння sin(x)=-1 має безліч коренів, а саме

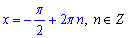
Рівняння cos(x)=-2 не має коренів, бо -2<1 (при ).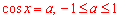
Рівняння arctg(x)=1 має єдиний корінь (бо -Pi/2<1<Pi/2), а саме x=tg(1).
Рівняння tg(x)=1 має безліч коренів, а саме

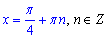
Рівняння (cos(x)-1)/sin(x)=0 не має коренів, оскільки

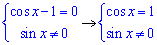
тобто

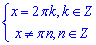
усі числа 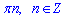містяться в 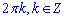, отже отримали суперечність

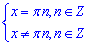
Відповідь: В.

Приклад 18.8 Розв'язати рівняння sin²(x)-sin(x)=0.

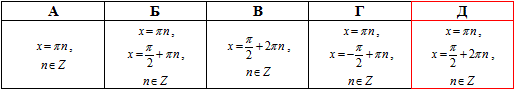
Розв'язання: Для зведення до системи тригонометричних рівнянь винесемо один синус за дужки.

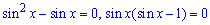
Останнє рівняння рівносильне системі рівнянь

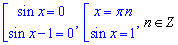
або після представлення розв'язку рівняння з синусом у вигляді

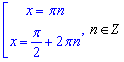
Звідси отримаємо частковий випадок, якщо sin(x)=0, то маємо розв'язок:

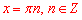
Відповідь: Д.

Графічно це рівняння можна побудувати в наступний спосіб
clear;
x=-pi/2:pi/50:2*pi;
y2=sin(x).^2-sin(x);
y1(1:126)=0;
figure (1), plot(x,y2,'r');
hold on;
plot(x,y1,'b');
xlim([-pi/2,2*pi]);
ylim([2,2]);
legend('sin(x).^2-sin(x)','0');
set(gca,'Xtick',-pi:pi/2:2*pi);
grid on;

В результаті отримаємо графіки функцій y=sin²(x)-sin(x), y=0:

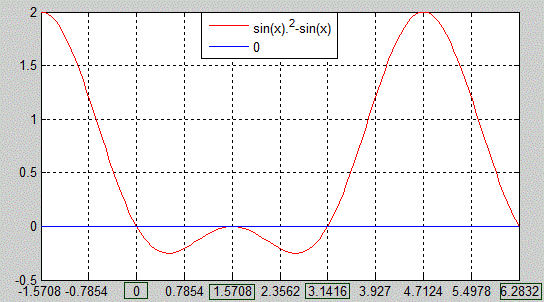
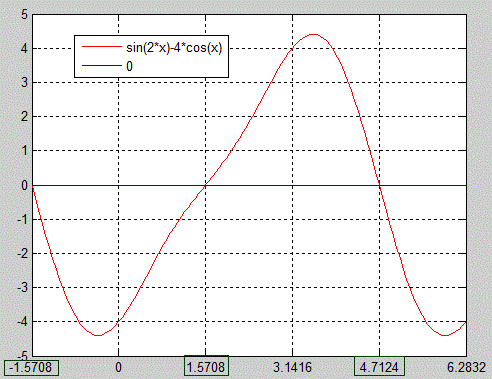
Приклад 18.9 Знайти корінь рівняння sin(2x)-4•cos(x)=0, який належить проміжку [2Pi,3Pi].

Розв'язання: Розписуємо синус подвійного кута, а далі виносимо в отриманому рівнянні косинус за дужки

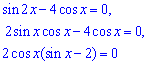
Останнє тригонометричне рівняння еквівалентне системі рівнянь

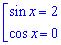
Оскільки виходимо за межі області визначення 2>1, то І рівняння коренів не має.
Розв'яжемо друге рівняння – cos(x)=0:

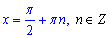
Отже, розв'язками заданого тригонометричного рівняння sin(2x)-4•cos(x)=0 є множина
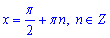(де n- довільне ціле число).
Очевидно, що корінь, який належить проміжку [2Pi;3Pi] є розв'язком при n=2:

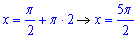
Відповідь: Б.

Для графічної побудови функцій y=sin(2x)-4•cos(x), y=0 потрібно замінити два рядки на такі:
y2=sin(2*x)-4*cos(x);
legend('sin(2*x)-4*cos(x)','0');
Перевагою графічного методу є в першу чергу бачити поведінку складних функцій, як наприклад різницю подвійного синуса та чотирьох косинусів.
При аналітичних обчисленнях Ви наосліп застосовуєте теоретичні знання + можете помилитися при тотожних перетвореннях.

Приклад 18.10 Розв'язати рівняння tg(x)=ctg(x).

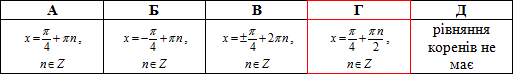
Розв'язання: Такого сорту приклади (де маємо дроби) слід аналізувати починаючи з області допустимих значень (ОДЗ) або принаймні вкінці наголосити, що розв'язок не суперечить ОДЗ. Запишемо ОДЗ:
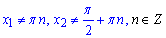(при них tg(x) і ctg(x) не існують).
Запишемо рівняння у вигляді tg(x)-ctg(x)=0.
Спростимо вираз tg(x)-ctg(x) за допомогою формули періодичності для котангенса та формули зведення:

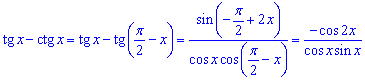
Випишемо значення, які не повинен приймати знаменник дробу.
При 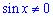отримаємо 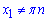, для 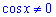отримаємо 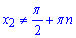, які враховані в ОДЗ.
Отже, отримали просте рівняння на рівність нулю косинуса подвійного кута –cos(2x)=0, або cos(2x)=0.
Його розв'язок має вигляд

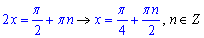
Відповідь: Г.

Щоб побудувати графічно різницю тангенса та котангенса в коді змінюємо три рядки
y2=tan(x)-cot(x);
set(gca,'Xtick',-pi:pi/4:2*pi);
legend('tan(x)-cot(x)','0');
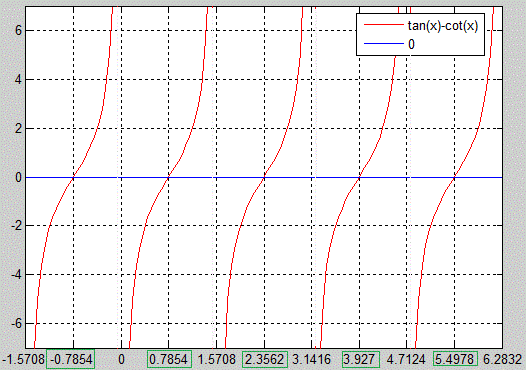
В результаті отримаємо ось такий графік

Приклад 18.11 Розв'язати рівняння cos(x)/(sin(x)-1)=0.


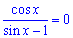
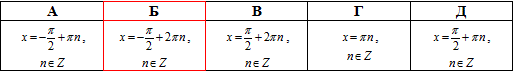
Розв'язання: Запишемо обмеження на ОДЗ: sin(x) ≠1, звідси

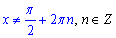
Отже, отримали просте рівняння cos(x)=0, з якого

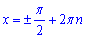
Враховуючи ОДЗ частину коренів відкидаємо та записуємо кінцеві значення:

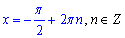
Відповідь: Б.

Для побудови графіків функцій y=cos(x)/(sin(x)-1),y=0 використаємо наступний код в пакеті мейпл
restart; with(plots):
> q1:=plot(cos(x)/(sin(x)-1),x=-2*Pi..2*Pi,color=red,thickness=2):
q2:=plot(0,x=-2*Pi..2*Pi,color=blue,thickness=2):
>display(q1,q2);
В результаті отриамаємо графчну ілюстрацію тригонометричного рівняння


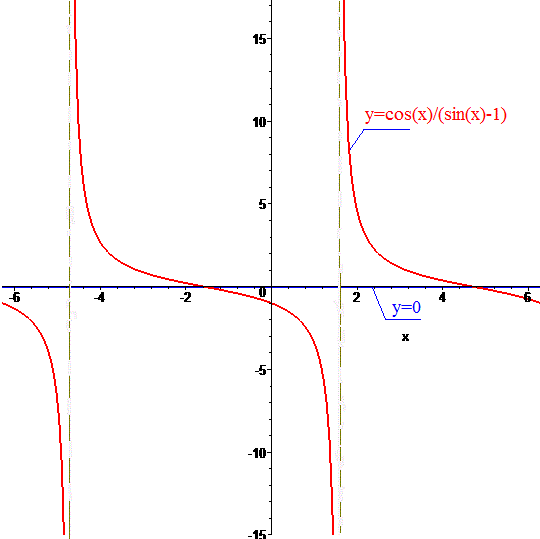
Ми не знаємо як прив'язати сітку кратну Пі чи меншим значенням, але відомо, що асимптоти виникають коли знаменник перетворюється в нуль:
sin(x)=1
а це кут Пі/2 плюс мінус період функцій 2Пі.

Приклад 18.12 Розв'язати рівняння √3sin(x)-cos(x)=0.

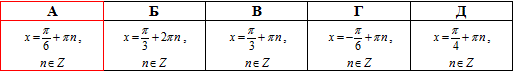
Розв'язання: Перетворимо вираз √3sin(x)-cos(x) до вигляду:

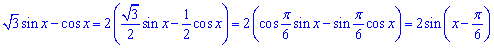
Тут використали штучний спосіб, а також формули зведення.
Іншого швидкого способу розв'язати подібні рівняння немає, тому добре запам'ятайте наведену схему.
Отримали просте рівняння

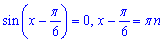
з якого корінь рівний

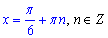
Відповідь: А.

В даному прикладі можемо побудувати як різницю функцій=0 так і кожну з них окремо.
У будь якому випадку точки перетину кривих будуть розв'язками тригонометричного рівняння.
Для різниці функцій код в мейпл має вигляд
restart; with(plots):
> q1:=plot(sqrt(3)*sin(x)-cos(x),x=-2*Pi..2*Pi,color=red,thickness=2):
q2:=plot(0,x=-2*Pi..2*Pi,color=blue,thickness=2):
> display(q1,q2);
Для побудови синусоїди і косинусоїди q1,q2 замінимо наступними рядками:
q1:=plot(sqrt(3)*sin(x),x=-2*Pi..2*Pi,color=red,thickness=2):
q2:=plot(cos(x),x=-2*Pi..2*Pi,color=blue,thickness=2):
Для того, щоб переконатися, що розв'язки в першому і другому випадку ті самі, наведемо графіки один під одним

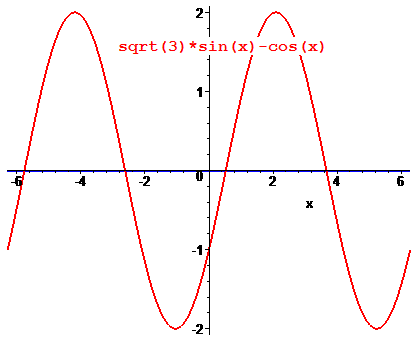
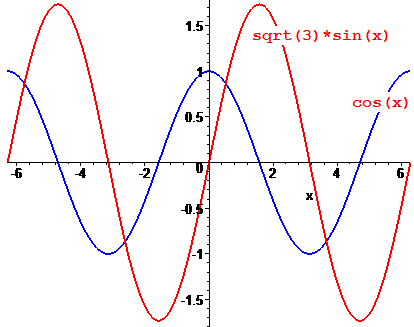
Що краще та наочніше вибирати Вам, але знати як аналітичні методи розв'язку тригонометричних рівнянь, так і графічні та числові не завадить нікому.

Готові відповіді на рівняння другого та старших порядків читайте в наступній публікації.