Сьогодні проаналізуємо останні 10 прикладів на перетворення тригонометричних виразів.
Приклади одні з важчих при проходженні ЗНО тестування та мало хто з Вас хотів би їх бачити на контрольній чи розрахунковій роботі. Однак такі завдання є і ми можемо переконати Вас, що обчислювати їх можливо, знаючи формули та методики розрахунків, які багато разів наводилися на попередніх уроках.
Завдання 7.40 Обчислити значення виразу
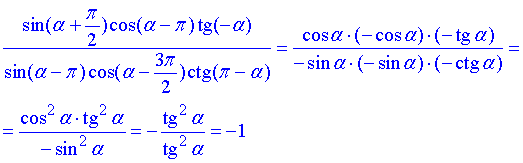
Для спрощення виразу використані знання періодичності синуса, косинуса, тангенса та котангенса, та симетрії функцій, що виражена в формулах зведення.
Подальші маніпуляції це всім відомі спрощення дробів.
Відповідь: -1.
Завдання 7.41 Спростити вираз
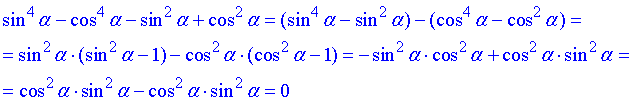
В даному прикладі перегрупували доданки та винесли за дужки квадрат косинуса.
В результаті в дужках отримали вираз, який легко дістати з основної тригонометричної тотожності:
сума квадратів синуса та косинуса рівна одиниці.
Такі перетворення доволі часто зустрічаються в тригонометрії, тому постарайтеся запам'ятати наведений прийом.
Відповідь: 0.
Завдання 7.42 Знайти значення виразу
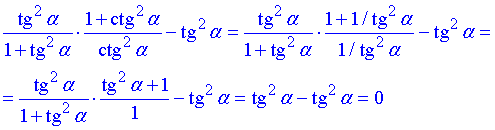
Для обчислення прикладу використали тотожність:
добуток тангенса на котангенс рівна одиниці.
Решта дій - це зведення до спільного знаменника та спрощення дробових виразів.
Відповідь: 0.
Завдання 7.43 Спростити вираз
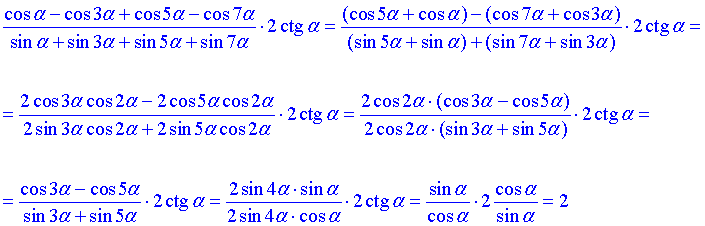
Даний приклад важкий в плані обчислень, оскільки треба бути добрим спеціалістом, щоб одразу знати, що та як перетворювати.
Проте знання наведеної схеми розрахунків дозволяє за кілька дій прийти до простого, а головне правильного результату.
Відповідь: 2.
Завдання 7.44 Спростити вираз
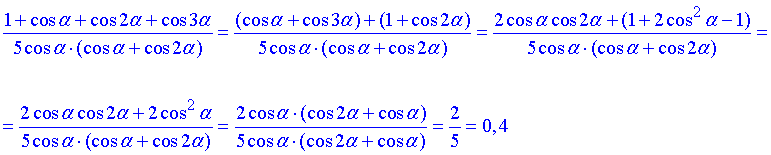
В чисельнику перегрупуємо косинуси, а далі перетворюємо доданки за допомогою формули зведення та косинуса подвійного кута.
Відповідь: 0,4.
Завдання 7.45 Маємо завдання на спрощення тригонометричного виразу, який зразу так і не ясно, як обчислювати.
Але схема вже раніш розглядалася: спершу використовуємо періодичність функцій, а далі розписуємо та сумуємо.
В результаті прийдемо до компактної відповіді.
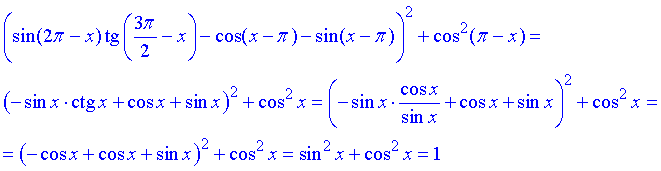
Відповідь: 1.
Завдання 7.46 Знайти значення виразу
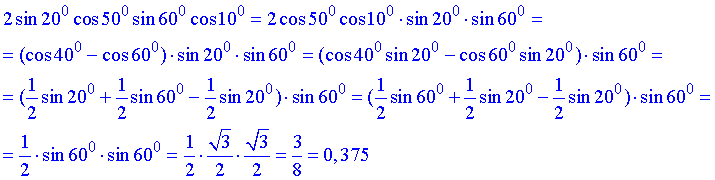
Завдання полягало в обчисленню добутку двох синусів та двох косинусів.
Після перегрупування та застосування формул зведення вдалося прийти до добутку синусів 60 градусів.
Решта доданків скоротилася внаслідок протилежних знаків.
Відповідь: 0,375.
Завдання 7.47 Знайти значення виразу
Задано суму ряду з косинусами в знаменнику. Спершу суму косинусів записуємо через добуток, а далі знаходимо суму ряду та сумуємо з останнім доданком
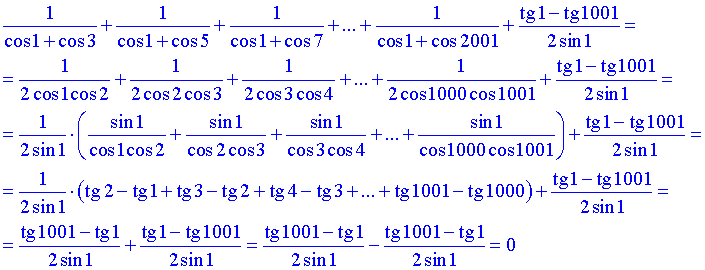
Тут використали формулу:
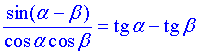
Відповідь: 0.
Завдання 7.48 Спростити вираз
Тут потрібно правильно перегрупувати доданки в чисельнику дробу, подальші обчислення теж вимагають певних маніпуляцій із застосуванням основних тригонометричних тотожностей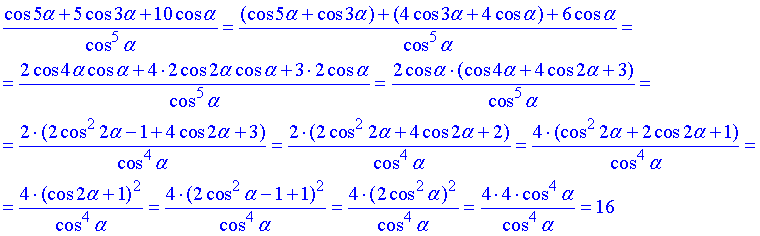 
Відповідь: 16.
Завдання 7.49 Обчислити синус подвоєного арктангенса мінус тангенс половини арккосинуса можливо, коли знати наступні формули
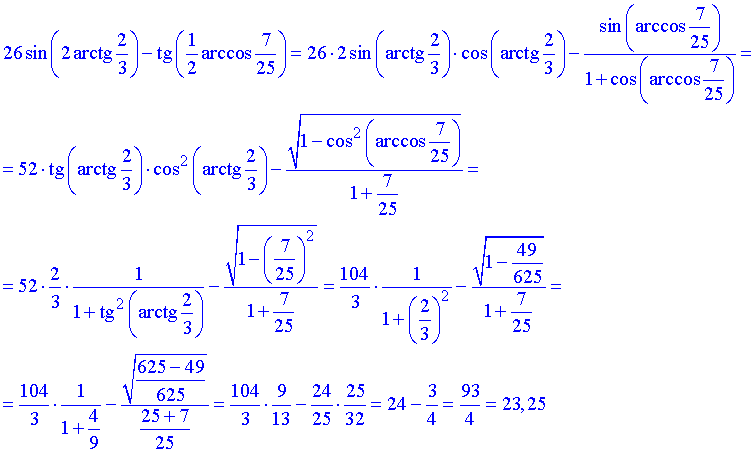
Приклад не з легких, але як бачите і такі тестові завдання можливо вирішити.
Відповідь: 23,25
Завдання 7.50 Якщо x=2*arcsin(1/6), то:
Розв'язування: Підставляємо аргумент та, використовуючи наведені далі формули, спрощуємо тригонометричні вирази
1) 18*cos(x), косинус подвійного арксинуса подамо через формулу косинуса подвійного кута.
А дальше працює відома формула, що синус від арксинуса рівний самому аргументу.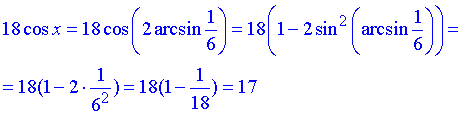
2) Тут потрібно визначити синус від подвійного арксинуса, що не важко, якщо скористатися формулою синуса подвійного кута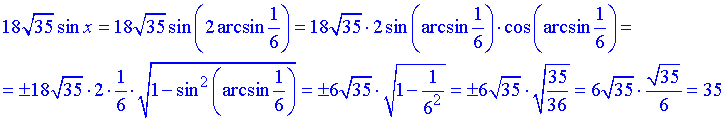 
Косинус від арксинуса раніше зустрічався, і вся суть перетворень полягає в переході від косинуса до синуса за допомогою формули, виведеної з основної тригонометричної тотожності.
Кут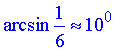 
знаходиться у І чверті, тому косинус арксинуса додатний 
.
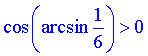Відповідь: 1) 17; 2) 35.
Надсилайте нам Ваші розв'язки на тему спрощення дробів і ми їх доповнимо до наявних відповідей, або оформимо у вигляді нових публікацій.
Далі переходимо до тригонометричних рівнянь та нерівностей.
