Обернені функції (арксинус, арккосинус, арктангенс, арккотангенс) необхідні для розв'язування тригонометричних рівнянь та нерівностей. Вам часто прийдеться мати справу з їх областями визначення та допустимих значень. Також слід розуміти, що всі формули, що тут зібрані для обернених тригонометричних формул вивчати на пам'ять не потрібно, це нічого не дасть. Набагато важливіше знати де їх знайти та як використати на практиці, щоб знайти правильний розв'язок поставленої задачі.
Інформація про обернені тригонометричні функції структурована за подібною схемою як для звичайних функцій. Спершу йдуть графіки арксинуса, арккосинуса, арктангенса, арккотангенса, щоб Ви візуально побачили з чим Вам прийдеться працювати. Далі основні властивості обернених тригонометричних функцій. В другій половині матеріалу наведені формули взаємозв'язку між оберненими і звичайними тригонометричними ф-ми.
Частину матеріалу Вам буде потрібно мати під рукою на практичних та розрахункових, інший ряд формул приведений для специфічних завдань, з якими навряд чи Ви будете мати справу.
Графіки і властивості обернених тригонометричних функцій
Арксинус y=arcsin(x)
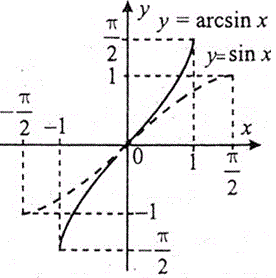
Графіки арксинуса, арккосинуса та решти 2 функцій утворюються перетворенням симетрії відносно прямої у = х.
Про це Ви часто можете прочитати в літературі, а от графіки не всюди є наведені. Тод переглядайте графіки та аналізуйте поведінку функцій.
Область визначення: D(y): x∈[-1;1].
Область значень: E(y):y∈[-Pi/2;Pi/2], тобто -Pi/2≤arcsin(x)≤Pi/2.
Функція непарна: arcsin(-x)=-arcsin(x).
Точка перетину з осями координат: (0;0)
Проміжки знакопостійності:
y>0, якщо x∈(0;1];
y<0, якщо x∈[-1;0).
Функція зростає при x∈[-1;1];
ymax=Pi/2 у точці xmax=1;
ymin=-Pi/2 у точці xmax=-1.
Арккосинус y=arccos(x)
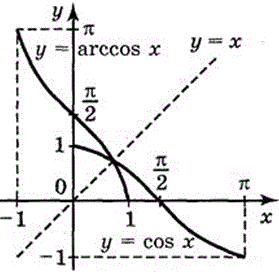
Область визначення: D(y):x∈[-1;1],
Область значень: E(y):y∈(0;Pi), тобто 0≤arccos(x)≤Pi.
Функція ні парна, ні непарна: arccos(-x)=-Pi-arccos(x).
Точки перетину з осями координат:
(0;Pi/2) на осі Oy, (1;0) на осі Ox;
Проміжки знакопостійності: y>0, якщо x∈[-1;1]
Функція спадає при x∈[-1;1];
ymax=Pi у точці xmax=-1;
ymin=0 у точці xmin=1.
Арктангенс y=arctg(x)
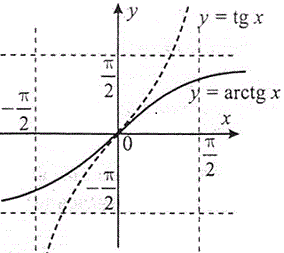
Область визначення: D(y):x∈R.
Область значень: E(y):y∈(-Pi/2;Pi/2), тобто –Pi/2<arctg(x)<Pi/2.
Функція непарна: arctg(-x)=- arctg(x).
Точка перетину з осями координат: (0;0).
Проміжки знакопостійності:
y>0, якщо x∈(0;+∞);
y<0, якщо x∈(-∞;0);
Функція зростає при x∈R.
Арккотангенс y=arcctg(x)
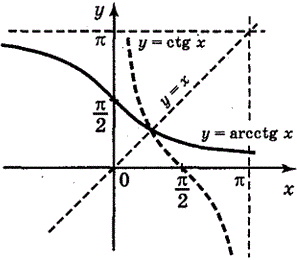
Область визначення: D(y):x∈R.
Область значень: E(y):y∈(0;Pi), тобто 0<arcctg(x)<Pi.
Функція ні парна, ні непарна: arcctg(-x)=Pi- arcctg(x)
Точка перетину з віссю Oy: (0;Pi/2);
вісь Ox не перетинає
Проміжки знакопостійності: y>0, якщо x∈R.
Функція спадає при x∈R.
Основні властивості обернених тригонометричних функцій часто використовують викладачі при підготовці тестів, щоб в короткий термін перевірити наскільки добре учні чи студенти засвоїли теоретичний матеріал. Тому такі властивості як ОДЗ, парність функцій, точки перетину Ви повинні знати для кожної з обернених тригонометричних функцій.
Основні формули для аркфункцій
Наведені формули для обернених тригонометричних функцій з однієї сторони розкривають їх властивості, з іншої показують взаємозв'язок між функціями.
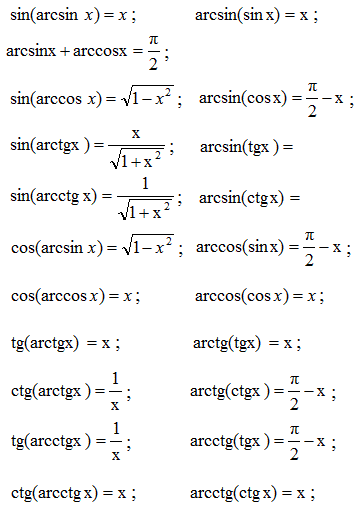
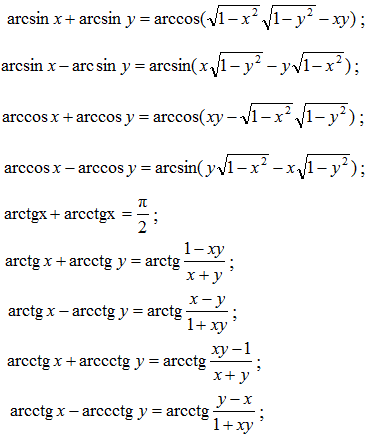
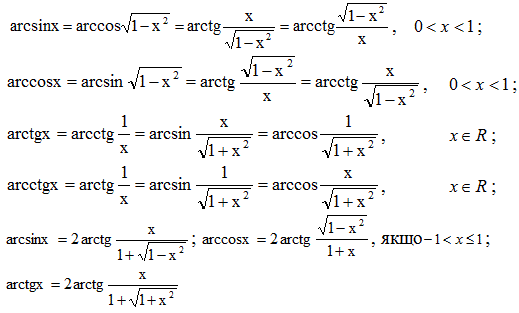
Вивід формул тут не давали оскільки він громіздкий і не всім потрібний. При бажанні такі розрахунки містяться на сторінках в інтернеті і Ви без проблем можете викачати їх. Практична ж сторона застосування обернених тригонометричних функцій до обчислення прикладів приводиться в наступних уроках.


