Інтегральна ознака Коші-Макларена: нехай загальний член ряду f(n) є монотонною, додатною спадною функцією від номера на проміжку [1,+∞).
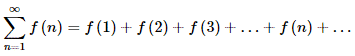
Тоді ряд f(n)=f(1)+f(2)+f(3)+…+f(n)+… збігається, якщо збіжний невластивий інтеграл  <∞
<∞
і розбігається, якщо інтеграл прямує до безмежності
 →∞.
→∞.
На практиці та в літературі часто опускають, що ця ознака також належить Макларену, тому Ви часто будете зустрічати «дослідити збіжність ряду за інтегральною ознакою Коші». Пам'ятайте, що це одна і та ж ознака збіжності.
Приклад 1. Дослідити на збіжність ряд
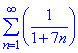
Розв'язування: Візуально бачимо, що члени ряду додатні та спадають з ростом номера. В такому випадку маємо право використати радикальну ознаку Коші для вияснення, чи ряд збіжний
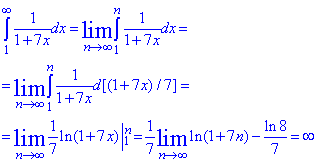
Оскільки інтеграл рівний безмежності, то ряд розбігається.
Приклад 2. Чи збіжний ряд
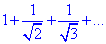
Розв'язування: З попередніх уроків Ви могли бути ознайомлені, що заданий ряд є рядом Діріхле із загальним членом an=1/√n з показником p=1/2<1, тому є розбіжним.
Доведемо це з допомогою радикальної ознаки Коші.
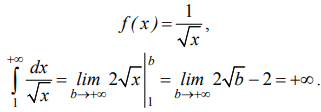
Інтеграл рівний безмежності, тому за правилом Коші він розбігається.
Приклад 3. Довести збіжність ряду
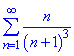
Розв'язування: Члени ряду монотонно спадають, тому необхідні умови для збіжності ряду виконуються. За достатню умову вибираємо ознаку Коші-Макларена. Для цього відповідний інтеграл розкриваємо шляхом заміни змінних
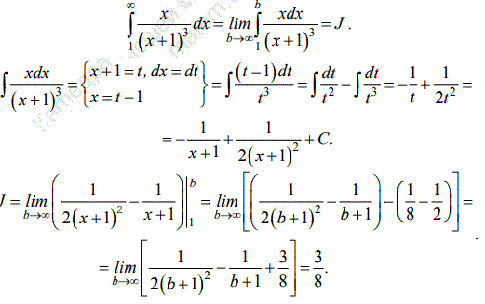
В результаті перетворень інтеграл int=3/8 скінченний, тому за інтегральною ознакою він збігається.
Приклад 4. Довести, що ряд розбігається
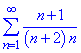
Розв'язування: Члени ряду по характеру збіжності можна порівняти з гармонійним рядом і довести, що він розбіжний. Але так як мета уроку, навчити Вас застосовувати інтегральну ознаку Коші, то переходимо до інтегрування відповідної ряду функції:
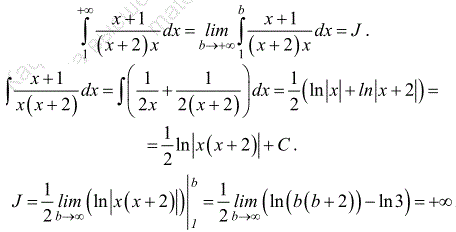
Інтеграл рівний безмежності, що є признаком розбіжності ряду.
Приклад 5. Дослідити на збіжність ряд
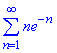
Розв'язування: Візуально бачимо лише, що члени ряду додатні:
експонента у від'ємному степені прямує до нуля.
Чи ряд спадає стане ясно лише з підстановки номерів, тому цей крок опустимо і перейдемо до перевірки чому рівний інтеграл.
Інтегруємо частинами
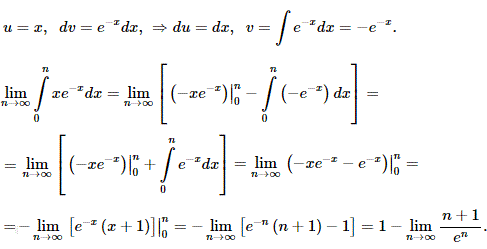
До останнього доданку застосовуємо правило Лопіталя
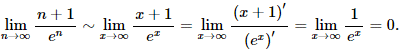
При підстановці в попередню формулу отримаємо інтеграл рівний 1, отже ряд за інтегральною ознакою збігається.
Приклад 6. За допомогою радикальної ознаки Коші довести, що ряд збіжний
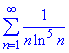
Розв'язування: Бачимо, що задано додатний спадний ряд з загальним членом
un=1/(n•ln^5(n)).
За інтегральною ознакою Коші знаходимо невластивий інтеграл.
Для розкриття інтегралу «ікс» зі знаменника вносимо під диференціал dx/x=d(ln(x)):
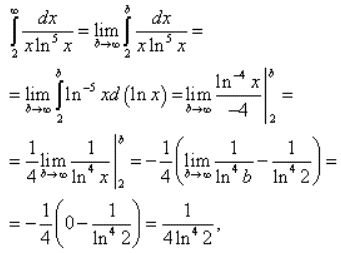
Інтеграл збіжний, отже за ознакою Коші ряд також збіжний, що і потрібно було довести.
Приклад 7. Чи збігається ряд

Розв'язування: Оскільки функція f(n)=1/(2n+3)^(7/6) визначена для всіх n≥1, додатна і спадна, то застосуємо інтегральну ознаку Коші збіжності ряду
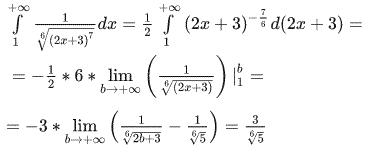
Оскільки інтеграл скінченний, то за Коші він збіжний.
Приклад 8. Дослідити на збіжність ряд
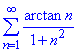
Розв'язування: Слід знати область значень оберненої тригонометричної функції арктангенс, щоб оцінити чисельник зверху:
arctan(n)<π/2.
Тоді за ознакою порівняння отримаємо
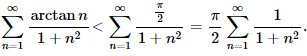
Застосовуючи інтегральну ознаку Коші, оцінимо збіжність ряду
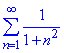
Відповідний інтеграл знаходимо шляхом внесення знаменника під диференціал
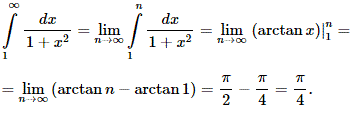
Оскільки невластивий інтеграл збіжний, то заданий ряд також збіжний.
На практиці Ви зустрінете малу кількість рядів, збіжність яких доцільно доводити за інтегральною ознакою збіжності. Такі ряди, як правило, легко інтегруються. Вивчіть інтегральну ознаку збіжності та використовуйте там де потрібно.


