Означення числового ряду, його збіжності. Геометрична прогресія та гармонічний ряд

Нехай задана нескінченна послідовність чисел u₁, u₂, u₃, ..., u_n, ... Нескінченна сума чисел виду u₁+u₂+u₃+...+u_n+...- називається числовим рядом, а числа u₁, u₂, u₃, ..., u_n, ...- членами ряду.
Ряд позначають так:
Вираз для n- го члена ряду при довільному натуральному n>0 , називається загальним членом ряду і позначається u_n.
Загальний член ряду можна задати формулою u_n=f(n), з допомогою якої записується довільний член ряду.

Суму n перших його членів позначають через S_n:
S_n=u₁+u₂+u₃+...+u_n.
і прийнято називати n-ою частинною сумою ряду.
Часткові суми ряду утворюють деяку числову послідовність його часткових сум S_n. Ряд називається збіжним, якщо збігається послідовність його часткових сум S_n, тобто якщо існує скінчена границя

Число S при цьому називають сумою ряду і записують

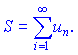
При цьому вважають також, що ряд збігається до числа S.
Якщо послідовність часткових сум ряду розбігається, то ряд називається розбіжним. У цьому випадку ряд не має суми.
Ряд, що складений з елементів геометричної прогресії називається геометричним рядом:

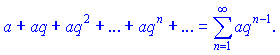
Число q — знаменник геометричної прогресії.
Позначимо S_n сума n перших членів прогресії та знайдемо її значення:


Звідси отримуємо формулу частової суми ряду


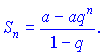
Якщо |q|<1, то суму ряду знаходимо за формулою

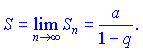
а геометричний ряд збігається.

Якщо |q|>1, то сума ряду прямує до безмежності при великих номерах

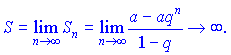
Якщо q=1, то сума теж розбіжна (прямує до безмежності)

Якщо q=-1, то маємо формулу суми, що залежить від номера

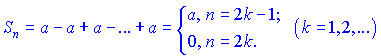
таким чином, послідовність часткових сум S_n - розбіжна.
Ряд вигляду

називається гармонічним рядом. Він розбіжний.
Числовий ряд вигляду

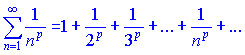
називається узагальненим гармонічним рядом. Доведено, що при p<=1 узагальнений гармонічний ряд розбігається, а при p>1 -ряд збігається.

Якщо ряд збігається, то різниця між сумою S і частинною сумою його S_n

називається n -им залишком ряду.
Залишок R_n ряду являє собою ту похибку, яка одержиться, якщо замість наближеного значення суми ряду S взяти суму перших n членів цього ряду. Але оскільки S є границя суми S_n, то для збіжного ряду виконується умова, що границя залишку прямує до нуля при номері прямуючому до безмежності

Таким чином, взявши достатньо велике число членів збіжного ряду, можна суму цього ряду обчислити з любою точністю. Звідси випливає, що основною задачею теорії рядів є дослідження збіжності ряду.