Окрім знакододатних рядів на практиці зустрічаються знакозмінні та знакопочергові ряди. Про них і піде мова в даній статті.
Ряд вигляду
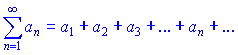
називається знакозмінним, якщо частина його членів приймає додатні значення, а решта - від'ємні.
Знакопочерговим називається ряд, сусідні члени якого мають протилежні знаки. У випадку, коли перший член знакопочергового ряду додатний, його можна подити у вигляді
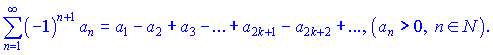
Ознака Лейбніца
Для дослідження збіжності ряду використовують ознаку Лейбніца: якщо члени знакопочергового ряду спадають по абсолютній величині та границя загального члена ряду рівна нулю
![]()
то ряд збіжний. При цьому сума ряду не перевищує значення його першого члена, якщо він додатній.
Для знакозмінного ряду існують поняття абсолютної та відносної збіжності.
Знакозмінний (знакопочережний) ряд збіжний абсолютно, якщо цей ряд та ряд утворений з модулів членів цього ряду збіжні одночасно.
Ряд називають умовно або неабсолютно збіжним у випадках, коли збіжний лише знакозмінний ряд, а ряд складений з абсолютних величин членів ряду розбігається.
Дослідження рядів на збіжність
Приклад 1. Дослідити які ряди збігаються абсолютно, умовно чи розбігаються
1) (9.131)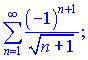
Розв'язок. Даний ряд знакопочережний, а також кожен наступний член по модулю менший за попередній
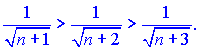
Знайдемо границю загального члену ряду
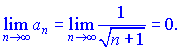
За ознакою Лейбніца ряд збіжний. Перевіримо ряд складений з модулів членів на абсолютну збіжність. Застосуємо ознаку Даламбера
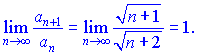
Дана ознака відповіді не дає. Застосуємо інтегральну ознаку Коші
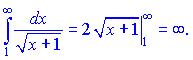
Ряд розбіжний, інтеграл рівний безмежності.
Оскільки знакопочережний ряд збіжний, а ряд з модулів розбіжний, то роглянутий ряд відносно збіжний.
2) (9.132)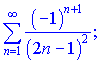
Розв'язок. Кожен наступний член ряду по модулю менший за попередній
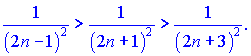
Границя загального члена рівна нулеві
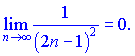
Ознака Лейбніца виконується.
Перевіримо ряд на абсолютну збіжність. Застосуємо інтегральну ознаку Коші
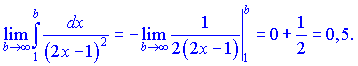
Вона підтверджує збіжність ряду. Вихідний ряд абсолютно збіжний.
3) (9.133)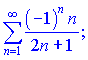
Розв'язок. Необхідна ознака збіжності не виконується, оскільки кожен наступний член ряду по модулю більший за попередній
![]()
За озакою Лейбніца ряд розбігається.
4) (9.134)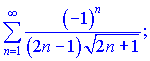
Розв'язок. Члени ряду по модулю спадають
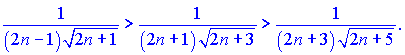
Обчислюємо границю un
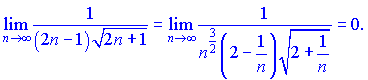
Границя рівна нулю, отже ряд збіжний за ознакою Лейбніца.
Перевіримо на абсолютну збіжність. З вигляду бачимо, що ознака Делабера нічого не дасть. Застосуємо інтегральну ознаку Коші. Після заміни змінних під інтегралом отримаємо гіперболічний арктангенс, який на межах інтегрування приймає обмежене значення
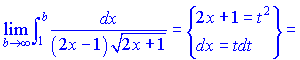
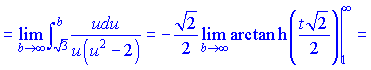
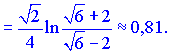
Даний ряд збіжний (Integal=0,81). Отже ряд абсолютно збіжний.
Приклад 2. Дослідити знакочережний ряд на збіжність.
а) 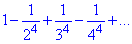
Маємо 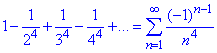
Нехай cn=1/n^4. Досліджувати цей ряд будемо за ознакою Лейбніца:
ряд 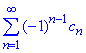 збігається, якщо границя n-го члена рівна нулю
збігається, якщо границя n-го члена рівна нулю 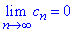 і cn>cn+1>0.
і cn>cn+1>0.
Перевірка показує, що умови виконуються
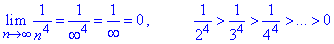
звідси слідує, що ряд 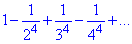 збігається.
збігається.
б) 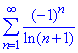
Досліджувати цей ряд будемо за ознакою Лейбніца:
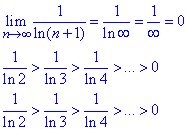
звідси слідує, що ряд 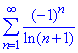 збігається, але умовно, бо ряд складений за модулем
збігається, але умовно, бо ряд складений за модулем 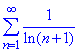 розбіжний.
розбіжний.
На цьому ознайомлення з ознакою Лейбніца завершено. Разом з ознаками для додатніх рядів Ви тепер можете перевіряти знакопочергові ряди на абсоюту збіжність. Впереді Вас чекає маса уроків, які в повній мірі дозволять Вам аналізувати та досліджувати числові та функціональні ряди.


