Задач на визначення міри кута багато не тільки в шкільній програмі, але й при вступі у ВУЗи та й на перших курсах навчання. Далі наведено 10 задач, в яких необхідно визначити кут. Подібних прикладів на обчислення кутів можна навести сотні, в більшості випадків вони не важкі і вимагають добрих знань простих властивостей кутів.
Задача 44.8 Який кут утворюють стрілки годинника о 16 годині?
А | Б | В | Г | Д |
1000 | 1100 | 1200 | 1300 | 1500 |
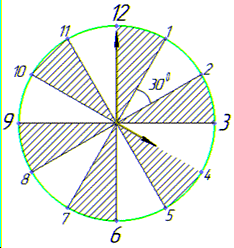
Розв'язування: Нехай циферблат годинника замінимо на круг з центром, з якого виходять хвилинна (довша) і годинна (коротка) стрілки.
Градусна міра круга дорівнює 3600.
Годинник розділений поділками на 12 рівних частин, градусна міра якої:
3600/12=300.
О 16 годині хвилинна стрілка стоятиме в початковому положенні (показуватиме 12), а годинна стрілка пройде рівно 4 частини круга і покаже 4.
Тому кут між стрілками о 16 годині становитиме:
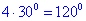
Відповідь: 1200 –В.
Задача 44.9 Між сторонами кута AOB проведено промінь OC так, що ∠AOC=2∠BOC.
Знайти кут AOC, якщо ∠AOB=540.
А | Б | В | Г | Д |
90 | 180 | 270 | 360 | 400 |
Розв'язування: Нехай градусна міра кута BOC дорівнює x, тобто ∠BOC=x.
Тоді градусна міра кута AOC дорівнює 2x, тобто ∠AOC =2x.
Градусна міра кута дорівнює сумі градусних мір кутів, на які він розбивається будь-яким променем, що проходить між його сторонами. Отже, ∠AOB=∠AOC+∠BOC=x+2x=3x.
Але за умовою задачі: ∠AOB=540, тобто
3x=540, звідси x=∠BOC =180 і ∠AOC=2x=360.
Відповідь: 360 – Г.
Задача 44.10 Бісектриса кута A утворює з його стороною кут, що дорівнює 300.
Знайти кут, суміжний з кутом A.
А | Б | В | Г | Д |
1500 | 1200 | 1650 | 1400 | 1700 |
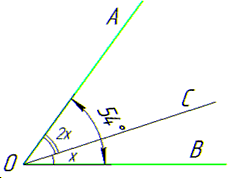
Розв'язування: Бісектриса кута – промінь, який виходить з вершини кута, проходить між його сторонами і ділить кут навпіл.
Нехай AK – бісектриса ∠BAC (кута A).
Тоді за умовою задачі ∠BAK=300 , а за означенням бісектриси:
∠BAC=2·∠BAK=600.
Нехай кут BAM суміжний з кутом BAC.
За теоремою: сума суміжних кутів дорівнює 1800 маємо:
∠BAM+∠BAC=1800 , звідси
∠BAM=180-∠BAC=1800-600=1200.
Відповідь: 1200 –Б.
Задача 44.17 Промінь OD ділить прямий кут AOB на кути AOD і BOD так, що
виконується рівність: 4∠AOD+3∠BOD=280. Знайти градусну міру кута AOD.
А | Б | В | Г | Д |
100 | 200 | 300 | 700 | 800 |
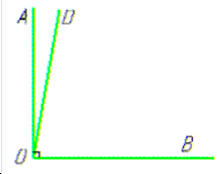
Розв'язування: За умовою задачі маємо: ∠AOB=900 (прямий).
Градусна міра кута дорівнює сумі градусних мір кутів, на які він розбивається будь-яким променем, що проходить між його сторонами.
Отже: ∠AOB=∠AOD+∠BOD.
Позначимо ∠AOD=x, тоді ∠BOD=900-x.
Підставимо отримані вирази в умову задачі:
4∠AOD+3∠BOD=280, тобто
4x+3(90-x)=280,
4x+270-3x=280,
4x-3x=280-270=100,
x=100.
Отже, ∠AOD=100.
Відповідь: 100 –А.
Задача 44.18 Який кут утворюють стрілки годинника о 15 годині 30 хвилин?
А | Б | В | Г | Д |
800 | 700 | 650 | 750 | 850 |
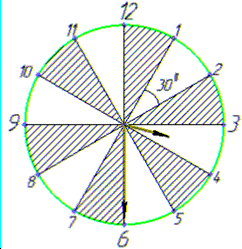
Розв'язування: Нехай циферблат годинника замінимо на круг з центром, з якого виходять хвилинна (довша) і годинна (коротка) стрілки.
Градусна міра круга дорівнює 3600.
Годинник розділений поділками на 12 рівних частин, градусна міра якої:
3600/12=300.
О 15.30 хвилинна стрілка стоятиме на позначці 6.
З початкового положення (позначка 12) ця стрілка зробить кут 1800.
Годинна стрілка пройде 3,5 частини круга і стоятиме між 3 і 4 посередині. З початкового положення (позначка 12) коротка стрілка зробить кут 3·300+150=1050.
Тому кут між стрілками о 15 годині 30 хвилин становитиме:
1800-1050=750.
Відповідь: 750 –Г.
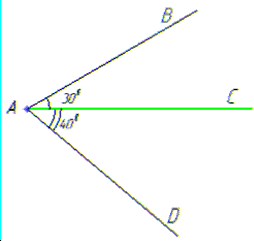
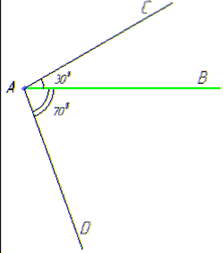
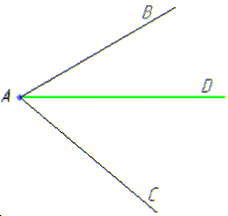
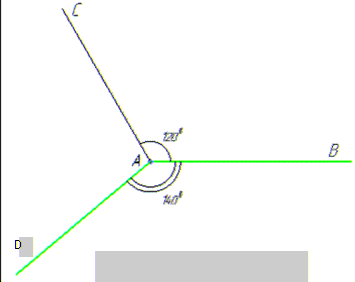
Задача 44.22 З точки A проведено промені AB, AC та AD.
Встановити відповідність між градусними мірами кутів (1–4) та розміщеннями променів (А–Д).
1. ∠BAC=300, ∠BAD=700, ∠CAD=400 | А. Промінь AD проходить між |
Розв'язування: Аксіома вимірювання кутів:
градусна міра кута дорівнює сумі градусних мір кутів, на які він розбивається будь-яким променем, що проходить між його сторонами.
1) ∠BAD=∠BAC+∠CAD=300+400=700, |
|
|
|
Задача 44.27 Скільки кутів, менших за розгорнутий, зображено на рисунку?
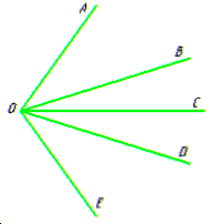
Розв'язування: Кут - це фігура, яка складається з точки - вершини кута і двох різних променів, що виходять із цієї точки, - сторін кута.
На рисунку позначимо п'ять променів, що виходять з однієї точки: OA, OB, OC, OD, OE, тоді випишемо усі кути, які утворилися:
∠AOB, ∠AOC, ∠AOD, ∠AOE, ∠BOC, ∠BOD, ∠BOE, ∠COD, ∠COE, ∠DOE - всього утворилося 10 кутів.
Тут можна помітити арифметичну прогресію:
нехай n - кількість променів, що виходять з однієї точки, тоді
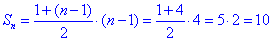
Відповідь:10.
Задача 44.28 З даної точки проведено три промені так, що кути між будь-якими двома з них рівні. Яка градусна міра кожного з цих кутів?
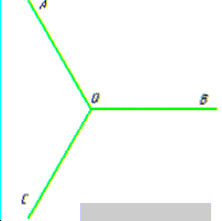
Розв'язування: З точки O проведемо три промені OA, OB і OC так, як сказано в умові задачі: що кути між будь-якими двома з них рівні, тобто
∠AOB=∠AOC=∠BOC.
Оскільки сума всіх кутів, які своїми сторонами (променями) розбивають площину дорівнює 3600, то отримаємо
∠AOB=∠AOC=∠BOC=360/03=1200.
Відповідь:1200.
Задача 44.31 Через точку перетину двох перпендикулярних прямих проведено третю пряму.
Знайти найменший з тупих кутів, що утворився в результаті
перетину, якщо найбільший з кутів дорівнює 1650.
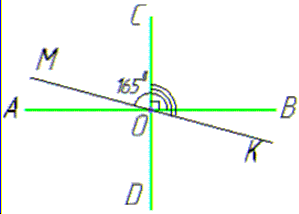
Розв'язування: Маємо дві перпендикулярні прямі AB та CD, які перетинаються в точці O, тобто ∠BOC=900.
Пряма MK перетинає прямі AB та CD в точці O так, що ∠BOM=1650 (за умовою).
∠AOB=180 (розгорнутий), тому ∠AOM=∠AOB-∠BOM=1800-1650=150.
∠BOK=∠AOM=15 як вертикальні.
∠COK=∠BOC+∠BOK=900+150=1050 - найменших з тупих кутів, що утворилися.
Відповідь:1050.
Задача 44.34Який кут утворюють стрілки годинника о 9 год 15 хв?
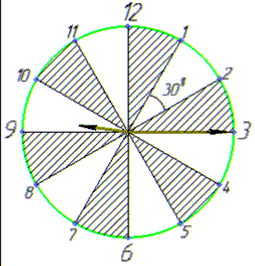
Розв'язування: Нехай циферблат годинника замінимо на круг з центром, з якого виходять хвилинна (довша) і годинна (коротка) стрілки.
Градусна міра круга дорівнює 3600.
Годинник розділений поділками на 12 рівних частин, градусна міра якої:
360/12=30.
О 9.15 хвилинна стрілка стоятиме на позначці 3.
З початкового положення (позначка 12) ця стрілка зробить кут 900.
Годинна стрілка пройде 9,25 частини круга і стоятиме між 9 і 10.
З початкового положення (позначка 12) коротка стрілка зробить кут
3·300-7,50=82,50.
Тому кут між стрілками о 9 годині 15 хвилин становитиме:
82,50+900=172,50.
Відповідь: 172,50 –Г.
Решта прикладів, що вимагають знаходження кута Ви знайдете в уроках цієї категорії.