Готові задачі на суміжні та вертикальні кути дозволять Вам не тільки ознайомитися з основними означеннями та властивостями, що стосуються таких кутів, а й навчать розв'язувати приклади подібні до наведених. Також ми покажемо Вам як оформляти такого класу завдання.
Пояснення до обчислень дуже важливі в першу чергу школярам, далі батькам та студентам. Думають, всі після прочитання залишаться задоволеними.
Приклади взяті із курсу ЗНО підготовки. Основні властивості суміжних та вертикальних кутів достатньо прості, тому на них зупинятися не будемо, а перейдемо зразу до розгляду розв'язків.
Задача 44.11 Сума двох кутів, суміжних з кутом B, дорівнює 800.
Знайти кут B.
А | Б | В | Г | Д |
500 | 1000 | 800 | 700 | 1400 |
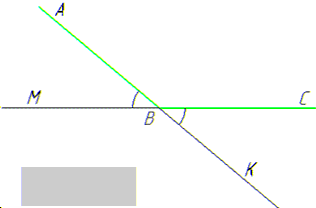
Розв'язування: Позначимо кут B через ∠ABC.
Тоді кути ∠ABM і ∠CBK є суміжними з кутом ABC, за умовою задачі
∠ABM +∠CBK =800.
Отже, кути ∠ABM і ∠CBK є вертикальними (за означенням) і рівними (за властивістю):
∠ABM=∠CBK,
звідси
2∠ABM=800, ∠ABM=∠CBK=400.
За теоремою: сума суміжних кутів дорівнює 1800 маємо:
∠ABM +∠ABC=1800, звідси ∠ABC=1800-∠ABM=1800-400=1400.
Отже, кут B дорівнює 1400.
Думаю, наведені пояснення не важко осмислити усім. Наступні приклади теж досить детально будуть розписані.
Відповідь: 1400 –Д.
Задача 44.12 На рисунку прямі AB, CD і MK перетинаються у точці O.
Знайти кут BOK, якщо ∠AOC=300, ∠MOD=1100.
А | Б | В | Г | Д |
700 | 600 | 200 | 400 | 500 |
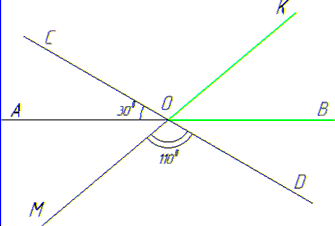
Розв'язування: Згідно з теореми: ∠COK=∠MOD=1100 як вертикальні кути.
Градусна міра кута дорівнює сумі градусних мір кутів, на які він розбивається будь-яким променем, що проходить між його сторонами. Отже,
∠AOK=∠AOC+∠COK=300+1100 =1400.
Згідно теореми: ∠AOK+∠BOK=1800 як суміжні кути.
Звідси отримаємо,
∠BOK=1800-∠AOK=1800-1400 =400.
Відповідь: 400 –Г.
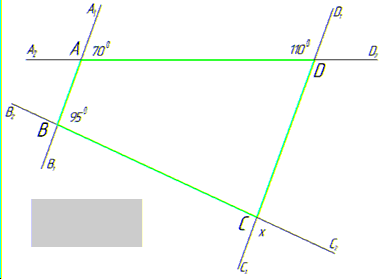
Задача 44.13 За даними рисунка знайти градусну міру кута x.
А | Б | В | Г | Д |
700 | 950 | 1100 | 850 | 750 |
Розв'язування: Нехай маємо кути ∠A1AD=700, ∠ADD1=110, ∠ABC=95.
Згідно теореми: ∠A1AD+∠BAD=1800і ∠ADD1+∠ADC=1800 як відповідні суміжні кути.
Звідси отримаємо,
∠BAD=1800-∠A1AD=1800-700=1100 і ∠ADC=1800-∠ADD1=1800-1100=700.
Оскільки ABCD – опуклий чотирикутник, то сума його внутрішніх кутів дорівнює 3600.
Тобто ∠BAD+∠ADC+∠DCB+∠ABC=360, звідси
∠DCB=360-(∠BAD+∠ADC+∠ABC)=3600-(1100+700+950)=850.
Згідно з теореми: x=∠C1CC2=∠DCB=85 як вертикальні кути.
Отже, x=850.
Відповідь: 850 –Г.
Задача 44.29 Різниця двох суміжних кутів менша за їхню суму на 200.
Знайти градусну міру меншого з цих кутів?
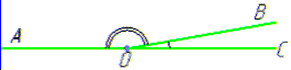
Розв'язування: Нехай ∠AOB і ∠BOC суміжні.
Тоді за теоремою: ∠AOB+∠BOC=1800.
Оскільки, за умовою задачі, їх різниця на 200 менша за їхню суму, то маємо
∠AOB-∠BOC=1600.
Позначимо: ∠BOC=x, тоді ∠AOB=x+1600. Тоді отримаємо,
∠AOB+∠BOC=1800,
x+1600+x=1800,
x+x=1800-1600,
2x=200, x=200:2=100,
остаточно∠BOC=100.
Відповідь:100.
Задача 44.30 Один з кутів, що утворилися в результаті перетину двох прямих, дорівнює сумі двох інших кутів. Знайти кут між прямими.
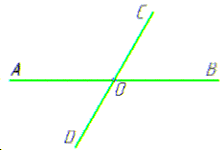
Розв'язування: Маємо дві прямі AB та CD, які перетинаються в точці O.
В результаті цього перетину утворилися пари суміжних і вертикальних кутів.
За умовою, ∠AOC=∠AOD+∠BOC, але за властивістю вертикальних кутів ∠AOD=∠BOC.
За властивістю суміжних кутів:
∠AOC+∠BOC=1800.
Позначимо ∠AOD=∠BOC=x, тоді ∠AOC=1800-x.
Тоді отримаємо,
1800-x=x+x,
1800=3x,
x=1800/3=600.
Отже, ∠AOD=∠BOC=600 і ∠AOC=1800-600=1200.
Тобто ∠AOD=∠BOC=600 - кут між прямими.
Відповідь:600.
Більше розв'язків задач на суміжні та вертикальні кути Ви можете знайти в сусідніх публікаціях.


