Вимірювання відрізків. Готові задачі

Задачі на визначення довжини відрізків одні з найлегших в курсі шкільної математики. При підготовці до вступу у Вузи вони також зустрічаються, серед них Вас можуть чекати наведені далі приклади. На всіх необхідних означеннях та аксіомах буде наголошено при обчисленні задач.

Задача 44.5 На відрізку AB позначено точку M таку, що AM=5 см, MB=15 см.
Знайти відношення AM:MB.

А	Б	В	Г	Д
1/4	1/3	1/2	1/5	1/6

Розв'язування: Довжина відрізка AB дорівнює сумі довжин відрізків AM=5 см і MB=15 см.
отже, AB=AM+MB=5+15=20 см.
Звідси,

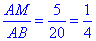
Відповідь: 1/4 –А.

Задача 44.6 На відрізку MK завдовжки 26 см вибрано точку O.
Знайти відстань між точками M та O, якщо вона на 12 см більша за відстань між точками O та K.

А	Б	В	Г	Д
7 см	13 см	12 см	19 см	14 см

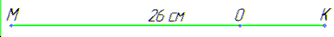
Розв'язування: Маємо MK=26 см, а довжина відрізка MO - відстань між точками M і O.
Нехай OK=x, тоді MO=x+12.
За аксіомою вимірювання відрізків: довжина відрізка дорівнює сумі довжин частин, на які він розбивається будь-якою його точкою,
отримаємо MO+OK=MK, тобто
x+12+x=26,
x+x=26-12,
2x=14,
x=7.
Отже, OK=7 см,
MO=7+12=19 см.
Відповідь: 19 см –Г.

Задача 44.7 На відрізку AB завдовжки 20 см позначено точки C та D такі, що AC=15 см, BD=17 см.
Знайти довжину відрізка CD.

А	Б	В	Г	Д
10,5 см	12,5 см	14 см	18 см	12 см

Розв'язування: За умовою задачі маємо: AB=20 см, AC=15 см і BD=17 см.
Довжина відрізка дорівнює сумі довжин частин, на які він розбивається будь-якою його точкою. Звідси знаходимо
BC=AB-AC=20-15=5 см;
AD=AB-BD=20-17=3 см;
CD=AB-(AD+BC)=20-(3+5)=12 см.
Відповідь: 12 см –Д.

Задача 44.15 Точка C належить відрізку AB завдовжки 9 см.
Знайти довжину відрізка BC, якщо 4·AC+3·BC=32 см.

А	Б	В	Г	Д
6 см	5 см	4 см	3 см	7 см

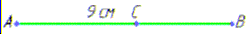
Розв'язування: За умовою задачі маємо: AB=9см.
Довжина відрізка дорівнює сумі довжин частин, на які він розбивається будь-якою його точкою: AB=BC+AC.
Нехай BC=x, тоді AC=9-x.
Підставимо отримані вирази в умову задачі:
4·AC+3·BC=32, тобто
4·(9-x)+3x=32,
36-4x+3x=32,
-x=32-36,
x=4.
Отже, BC=4 см.
Відповідь: 4 см –В.

Задача 44.16 Відрізок завдовжки 72 см поділили на 6 рівних частин.
Знайти відстань між серединами крайніх частин.

А	Б	В	Г	Д
62,5 см	60,6 см	58,6 см	63 см	60 см

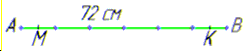
Розв'язування: Нехай маємо відрізок AB=72см.
Поділимо його на шість рівних частин, тоді довжина кожної такої частинки: AB:6=72:6=12 см.
Позначимо відрізок MK - відстань між серединами крайніх частин, тоді AM+BK=12 см
(тобто становить довжину однієї частинки відрізка), звідси
MK=AB-(AM+BK)=72-12=60 см.
Відповідь: 60 см –Д.

Задача 44.21 Встановити відповідність між рівностями (1–4) та розміщенням точок на
прямій (А–Д).

1. AC=7 см, BC=3 см, AB=10 см
2. AC=7 см, BC=3 см, AB=9 см
3. AC=12 см, BC=4 см, AB=8 см
4. AC=BC-AB

А. Точка B лежить між точками A та C.
Б. Точка A лежить між точками B та C.
В. Жодна з точок A, B та C не лежить між
двома іншими.
Г. Точка C лежить між точками A та B.
Д. Кожна з точок A, B та C лежить на прямій
між двома іншими.

      Розв'язування:   Аксіома вимірювання відрізків:
довжина відрізка дорівнює сумі довжин частин, на які він розбивається будь-якою його точкою

1) AB=AC+BC=7+3=10 (см), тому
точка C лежить між точками A та B                                        Г;

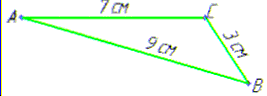
2) 9=AB≠AC+BC=7+3 (см), але сума двох відрізків більша за третій, тому
жодна з точок A, B та C не лежить між двома іншими         В;

3) AC=BC+AB=4+8=12 (см), тому
точка B лежить між точками A та C                                        А;

4) AC=BC-AB, звідси BC=AC+AB, тому
точка A лежить між точками B та C                                        Б.

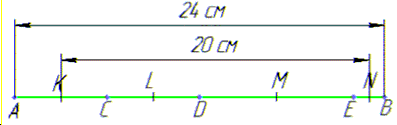
Задача 44.26 Відрізок завдовжки 24 см поділили на чотири нерівні відрізки. Відстань між серединами крайніх відрізків дорівнює 20 см.
Знайти відстань між серединами середніх відрізків.

Дано:
AB=24см,
KN=20см.

Знайти:
LM.

Розв'язування: За умовою задачі маємо:
AK=KC, EN=NB.
Тоді
AK+NB=AB-KN=24-20=4 см, звідси KC+EN=4 см.
Отже, CE=KN-(KC+EN)=20-4=16 см.
За умовою задачі маємо:
CL=LD, DM=ME.
Тоді

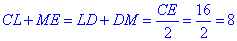
8 см - відстань між серединами середніх відрізків.
Відповідь:8.