Відстань від точки до площини — це довжина найкоротшого вектора, проведеного до площини. Оскільки таким вектором є перпендикуляр, то відстань рівна довжині перпендикуляра.
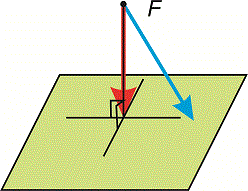
Формула відстані до площини
На практиці площину задають рівнянням Ax + By + Cz + D = 0. Точка в просторі (3D) характеризується трьома координатами F(x0, y0, z0). Формула Відстань від точки до площини знаходять за формулою
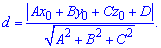
Вона виводиться аналогічно до формули відстані від точки до прямої на площині (2D) і геометрично рівна проекції будь-якого вектора проведеного з точки до площини на нормальний вектор площини (див. рис).
На практиці ніякої побудови чи аналізу виконувати не потрібно. Просто підставити дані у формулу і порахувати. Обчислення не надто складні, однак вартує користуватися калькулятором для обчислення кореня та ділення на нього. Решта дій можна виконати без допоміжної техніки.
Приклади знаходження відстані до площини
Приклад 1. Знайти відстань від точки F(1; 2; -1) до площини x-2y+3z-7=0.
Розв'язання: Застосовуємо формулу відстані від точки до площини
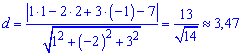
Відстань рівна 3,47 умовних одиниці.
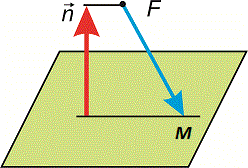
Приклад 2. Знайти відстань від точки M(3; 1; 2) до площини 2x+y-z+5=0.
Розв'язання: Підставляємо значення у формулу та знаходимо відстань
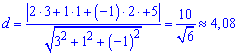
Ось так легко обчислили відстань.
Приклад 3. Трикутна піраміда задана вершинами A(1; -1; 2), B(3; 5; 1), C(2; 4; 0), D(8; 1; 3). Знайти висоту піраміди, проведеної з вершини D до основи.
Розв'язання: Складемо рівняння площини через три точки . Для цього виберемо довільну точку M(x; y; z) із площини і побудуємо три вектори
AM(x-1; y+1;z-2);
AB(3-1;5+1; 1-2)=(2; 6; -1);
AC(2-1;4+1; 0-2)=(1; 5; -2).
Знайдемо мішаний добуток векторів площини
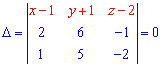
Розпишемо визначник за елементами першого рядка
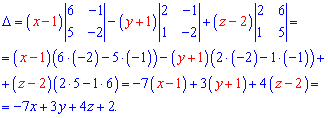
Канонічне рівняння площини наступне
-7x+3y+4z+2=0.
Маючи рівняння і точку D(8; 1; 3) відстань обчислюємо за формулою
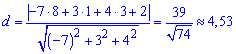
Висота піраміди 4,53 умовні одиниці.
Калькулятор відстані в Maple
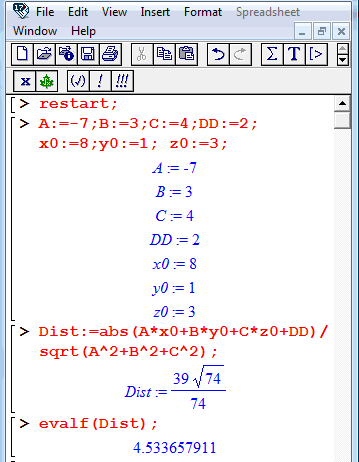
Якщо часто доводиться шукати відстань і є можливість написати калькулятор в математичному пакеті чи певній мові програмування то варто це зробити. По- перше Ви поглибите знання з програмування чи користування математичними пакетами. З другої сторони, написавши алгоритм обчислень один раз, Ви зможете розв'язати багато задач, змінюючи лише вхідні дані. В пакеті Маple код калькулятора для обчислення відстані від точки до площини матиме вигляд
> restart;
> A:=-7;B:=3;C:=4;DD:=2;x0:=8;y0:=1; z0:=3;
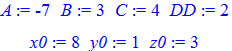
> Dist:=abs(A*x0+B*y0+C*z0+DD)/sqrt(A^2+B^2+C^2);
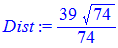
> evalf(Dist);
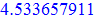
За алгоритмом знаходили розв'язок останнього прикладу. Сама ж програма Maple має вигляд
Після всього матеріалу Ви мабуть тепер знаєте, як знайти відстань від точки до площини. Запам'ятайте її та використовуйте там де цього вимагає практика.


