Скласти рівняння прямої на площині можна у випадках, коли відомі:
- точка, що належить прямій і перпендикулярний вектор до прямої;
- точка на прямій і вектор, паралельний до прямої;
- точка з прямої і кутовий коефіцієнт прямої;
- дві точки на прямій.
Рівняння прямої, що проходить через задану точку перпендикулярно до заданого вектора
Нехай пряма проходить через задану точку М0(х0, у0) перпендикулярно до вектора нормалі n = (A, B).
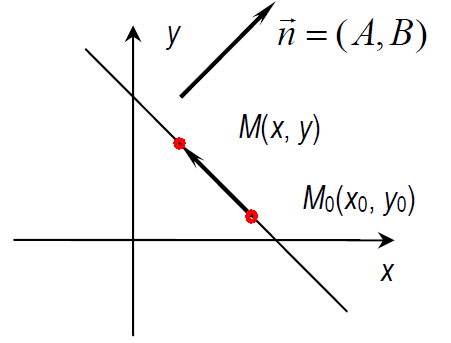
Візьмемо будь-яку точку М(х, у) прямої і запишемо умову перпендикулярності векторів М0M
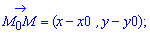та n (
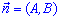) у векторній формі
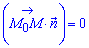
та координатній
А(х − х0) + B(y − у0) = 0.
Рівняння описує пряму, що проходить через задану точку М0(х0, у0) перпендикулярно до заданого вектора n = (A,B).
Окремі випадки рівняння прямої
- при x0 = y0 = 0 пряма проходить через початок координат. Її рівняння:
Ах + Ву = 0; - При B = 0, A відмінне від 0 одержуємо рівняння вертикальної прямої: х = х0;
- при A = 0, B відмінне від 0 одержуємо рівняння горизонтальної прямої: y = y0.
З рівняння прямої, згрупувавши доданки одержимо загальне рівняння прямої
Аx+Bx-A х0 - Bу0=0
або
Ах + Ву + D = 0.
Із запису випливає, що пряма є алгебраїчною лінією першого порядку (змінні x, y містяться в першому степені). Також, можна помітити, що у загальному рівнянні прямої коефіцієнти A і B при змінних х, y є координатами вектора нормалі до прямої.
Рівняння прямої, що проходить через задану точку паралельно заданому вектору
Маємо задану точку М0(х0, у0) на прямій, яка паралельна заданому вектору a = (l,m).
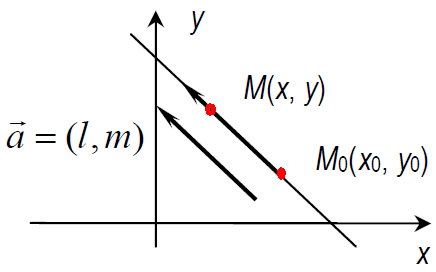
Для довільної точки з прямої М(х, у) повинні виконуватися умови колінеарності векторів
a = (l,m) і M0M=( x − x0 , y − y0)
(x − x0)/l=( y − y0)/m.
З цих умов і складаємо рівняння прямої
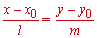
Рівняння прямої, що проходить через дві задані точки
Нехай дві точки М1(х1, у1), M2(х2, у2) з прямої. Виберемо на прямій біжучу точку М(х, у) і складемо рівняння прямої з умови колінеарності векторів
M1M = (x − x1, y − y1) і M1M2 = (x2 − x1, y2 − y1)
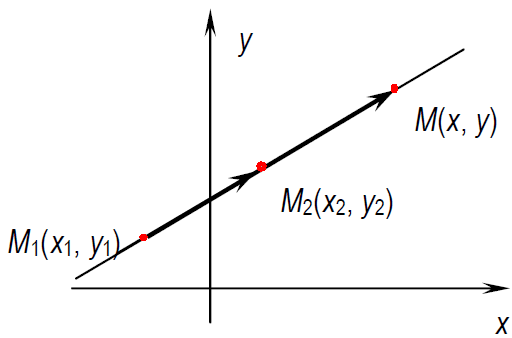
(x − x1)/ (x2 − x1)= (y − y1)/( y2 − y1)
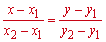
Формула прямої, що проходить через дві точки досить часто застосовується на практиці, тому вивчіть її на пам'ять.
Рівняння прямої у відрізках на осях
Нехай маємо пряму, що відтинає на осях координат Ox, Oy не рівні нулю відрізки a, b (див. рис.).
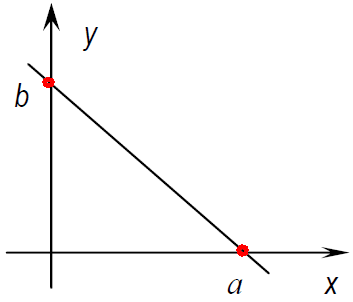
Якщо підставити у рівняння координати точок перетину прямої з осями М1(a, 0), M2(0, b) то одержуємо рівняння прямої у відрізках на осях:
x/a+y/b=1.
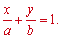
Рівняння прямої з кутовим коефіцієнтом
Нехай маємо пряму нахилену під кутом α ≠ π/2 до осі абсцис Ох.Число k=tgα називається кутовим коефіцієнтом прямої.
Візьмемо задану точку М0(х0, у0) і біжучу точку М(х, у) прямої та запишемо кутовий коефіцієнт прямої через прирости координат
k=tgα=(x − x0).( y − y0)
З цього співвідношення складаємо рівняння прямої, що проходить через задану точку М0(х0, у0) і має кутовий коефіцієнт k:
y − y0 = k(x − x0 ).
Поклавши x0 = 0 отримаємо рівняння прямої з кутовим коефіцієнтом:
y = kx + b
де b = y0 – відрізок, що відтинається прямою на осі Оу.
Розглянемо декілька прикладів.
Приклад 1. Скласти рівняння прямої, яка проходить через точку A(1;2), B(5;7).
Розв'язання: Підставимо координати точок у формулу прямої
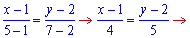
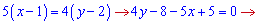
4y − 5x-3=0 – шукане рівняння прямої.
Не буде помилкою, якщо Ви поміняєте координати початку і кінця вектора AB місцями
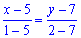
Тільки в цьому випадку в знаменнику матимемо від'ємні значення і доведеться витратити більше часу на обчислення.
Дане завдання можна зробити через рівняння прямої з кутовим коефіцієнтом
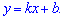
Маємо дві точки, відповідно при підстановці отримаємо два рівняння для визначення двох невідомих
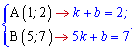
Систему рівнянь розв'язувати легко. З першого рівняння виражаємо b і підставляємо у друге
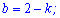
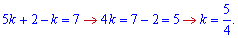
Підставимо знайдену невідому у перше рівняння
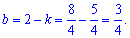
Остаточне рівняння прямої
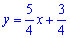
або
4y − 5x-3=0
що ідентично знайденому вище.
Приклад 2.Складіть рівняння прямої, яка проходить через точку A(-1;3) і паралельна прямій 3х-2у-1=0.
Розв'язання: Даний приклад можна розв'язати кількома способами.
1 спосіб. Зведемо рівняння прямої до прямої з кутовим коефіцієнтом
3х-1=2y; y=3/2*x-1/2.
Оскільки прямі паралельні то кутові коефіцієнти в них рівні
k=3/2; y=3/2*x+c.
підставимо точку і знайдемо невідому
3=3/2*(-1)+c;c=3+3/2=9/2.
Підставимо сталу у рівняння прямої
y=3/2*x+9/2 або 3x-2y+9=0.
2 спосіб
Оскільки прямі паралельні то коефіцієнти при невідомих в них пропорційні. Рівняння паралельної прямої матиме вигляд
3х-2у+d=0.
З умови проходження прямої через точку знаходимо невідому
3*(-1)-2*3+d=0;
d=6+3=9
та підставляємо у рівняння прямої
3х-2у+9=0.
Як бачите обчислення достатньо прості, потрібно лише знати властивості прямої.
Приклад 3.Знайдіть пряму, яка проходить через точку A(3;-5) і нахилена під кутом 45 до осі абсцис.
Розв'язання: Обчислимо кутовий коефіцієнт прямої
K=tan(45)=1.
Отже, рівняння прямої має вигляд
y=x+c.
Знайдемо невідому, підстановкою точки A(3;-5)
-5=3+c;
c=-5-3=-8.
Підставимо невідому в рівняння прямої y=x-8.
Приклад 4.Знайдіть пряму, яка рівновіддалена від точок A(2;5), B(8;11)
Розв'язання: Рівновіддалена від двох точок, означає, що проходить посередині відстані між A і B та перпендикулярна до вектора A, B.
Знайдемо середню точку між A і B
С=(A+B)/2=((2+8)/2;(5+11)/2)=(5;8).
Складемо рівняння прямої, що проходить через A і B
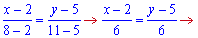
x-2=y-5; y=x+3.
Умова перпендикулярності прямих має вигляд
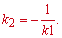
Для знайденої прямої кутовий коефіцієнт рівний одиниці, для перпендикулярної до неї – k=-1.
Залишається скласти рівняння прямої, що проходить через точку С= (5;8) з кутовим коефіцієнтом k=-1
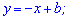
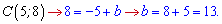
Підставимо знайдене значення у рівняння прямої
y=-x+13.
Після теоретичного матеріалу та практики Ви знаєте, як скласти рівняння прямої на площині. Користуйтеся наведеними формулами прямої та вибирайте оптимальний для себе метод розв'язування задач.
