Нехай прямі Lo та L1 задано канонічними рівняннями
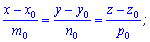
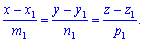
Кут між двома прямими phi в просторі вимірюється кутом між їхніми напрямними векторами
s1(m0; n0; p0) і s2(m1; n1; p1).
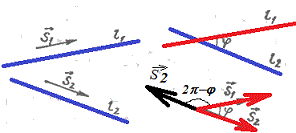
При цьому слід зазначити, що, вибравши на одній із прямих напрямний вектор, напрямлений в протилежну сторону, дістанемо другий кут, який доповнює перший до повного (2Pi).
Формула кута між прямими в просторі
Косинус кута рівний
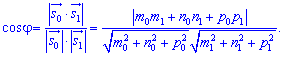
сам кут визначаємо через арккосинус
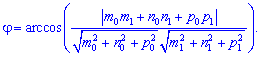
Ця формула визначає кут, на який треба повернути одну пряму в напрямку іншої, щоб вони наклалися.
За властивістю косинуса, умова перпендикулярності векторів слідує з формули
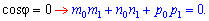
Умова паралельності прямих в просторі ідентична до умови на площині – напрямні вектори мають бути пропорційні.
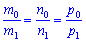
Всі ці формули кутів справедливі, якщо прямі мають канонічний вигляд, однак на практиці прямі можуть бути задані перетином двох площин
A1x+B1y+C1z+D1=0.
A2x+B2y+C2z+D1=0.
або параметрично
x=a0+a1*t;
y=b0+b1*t;
z=c0+c1*t.
В цих випадках, напрямний вектор прямої перетину площин знаходять через векторний добуток напрямних до площин
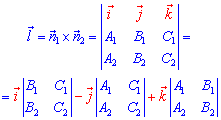
а для параметрично заданої прямої в просторі він рівний коефіцієнтам при параметрі
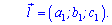
Для подальших обчислень кута застосовують наведені вище формули.
Приклади на знаходження кута
Приклад 1. Знайти кут між прямими, які задані рівнянням
(x-5)/2=(y+3)/(-1)=(z-1)/5 ;
-x=(y-2)/3=(z+3).
Розв'язання: Записуємо напрямні вектори прямих l1(2; -1; 5), l2(-1; 3; 1).
Підставимо у формулу кута
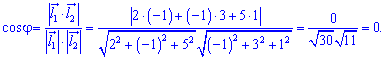
Косинус рівний нулю, значить прямі перпендикулярні.
Приклад 2. При яких значеннях параметрів m та n, прямі паралельні
x/2=(y-1)/m=(z+2)/3; (x+1)/n=(y-2)/3=z/6.
Розв'язання: Записуємо умову паралельності прямих
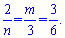
З даного співвідношення знаходимо шукані параметри
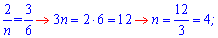
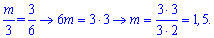
При m=1,5 та n=4 прямі паралельні між собою.
Приклад 3. Знайти кут між прямі, які задані перетином площин
3x-2y+z+4=0, x+5y-7z=0
та параметричним рівнянням
x=3-2t; y=5t-6;z=7-1t.
Розв'язання: Знаходимо напрямний вектор першої прямої через векторний добуток напрямних площин
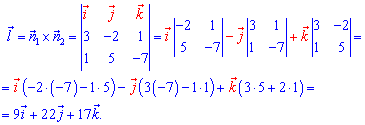
До прямої, яка задана параметрично напрямний вектор буде наступним
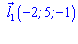 .
.
Далі застосовуємо формулу кута
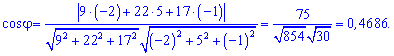
Застосовуємо обернену функцію
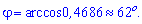
Отримали кут рівний 62 градуси.
Косинус рівний нулю, значить прямі перпендикулярні.
Калькулятор кута між прямими
З обчислень бачите, що доводиться обчислювати корені, тому варто мати під рукою калькулятор. Для спрощення обчислень пропонуємо скористатися вже готовим калькулятором, який обчислює кут між прямими на площині і в n- вимірному просторі та виводить пояснення до розрахунків.
В меню вибираєте пункт "вектори"- "кут між векторами".
Задаєте розмірність простору та вводите координати напрямних векторів
і після обчислень виписуєте результати знаходження кут.

Результати достатньо детально розписані, тому для багатьох будуть своєрідною підказкою в розрахунках. Завантажити математичний калькулятор YukhymCalc Ви можете за вказаним посиланням.


